
Dynamics of Rigid Bodies Formula : Dynamics of rigid bodies refers to the branch of classical mechanics that deals with the motion of objects that maintain a constant shape and size under the influence of external forces. In other words, it involves the study of how rigid bodies move and respond to forces and torques (rotational forces) applied to them.
Understanding this topic is important because it is a part of NEET 2024 Syllabus . Read this and improve your NEET UG 2024 preparation level.Dynamics of Rigid Bodies formula for NEET
The Dynamics of Rigid Bodies Formula includes Newton's laws of motion to describe the translational and rotational motion of the objects. Translational motion involves the linear movement of the object as a whole, while rotational motion involves the object's rotation about a fixed axis. Together, these motions are collectively described as the motion of a rigid body.Translational Motion - Translational motion refers to the movement of an object in which every point of the object moves along parallel paths. In translational motion, the entire object moves from one place to another without changing its orientation.
Newton's Second Law: F = ma, where F is the net force, m is the mass, and a is the acceleration. Linear Momentum: p = mv, where p is the linear momentum, m is the mass, and v is the velocity.Rotational Motion - Rotational motion, is the movement of an object in a circular path around a fixed point or axis. In rotational motion, the object spins or rotates about a central point. Each point of the object moves in a circular path, and the object changes orientation.
Moment of Inertia Definition
The moment of inertia, often denoted as I, is a measure of an object's resistance to changes in its rotation. It describes how the mass of an object is distributed with respect to its axis of rotation. A higher moment of inertia implies that more torque is required to produce the same angular acceleration. The formula for the moment of inertia depends on both the mass of the object and how this mass is distributed relative to the rotation axis.Basic Formula Moment of Inertia
The basic formula for the moment of inertia (I) of a point mass m rotating about an axis at a perpendicular distance r from the axis is:I=mr 2
This formula expresses the rotational inertia of a single-point mass. For more complex objects or systems, where mass is distributed continuously or there are multiple masses, the moment of inertia is determined by summing or integrating the contributions of each mass element along the object.Moment of Inertia for Different Objects
It will be interesting to know the concept of the Moment of Inertia for Different Objects to understand the Dynamics of Rigid Bodies formula because it is different for different shapes and sizes. Observe the expression given for the particular shapes and sizes in the given table.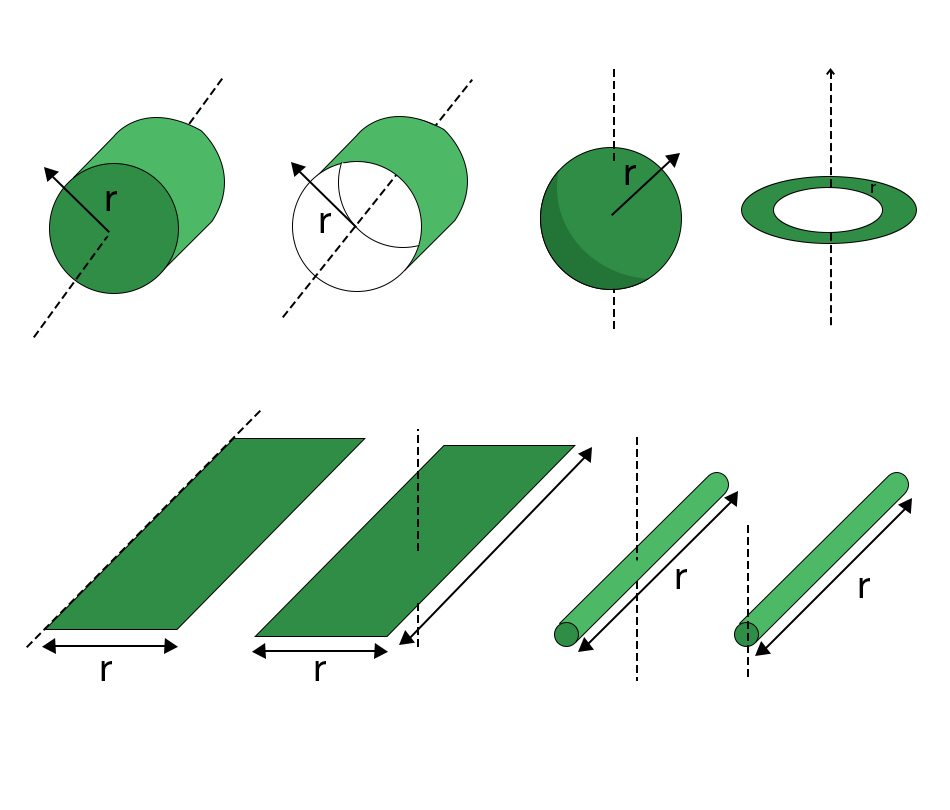
| Moment of Inertia for Different Objects | ||
|---|---|---|
| Object | Axis of Rotation | Moment of Inertia Formula |
| Point Mass | Axis passing through the mass | I = mr^2 |
| Thin Rod (about end) | Axis perpendicular to the rod | I = (1/3)mL^2 |
| Thin Rod (center) | Axis perpendicular to the rod | I = (1/12)mL^2 |
| Rectangular Plate | Axis through the center, parallel to sides | I = (1/12)m(a^2 + b^2) |
| Hollow Cylinder | Axis through the center | I = (1/2)m(R 1 ^2 + R 2 ^2) |
| Solid Cylinder | Axis through the center | I = (1/2)mR^2 |
| Hollow Sphere | Axis through the center | I = (2/3)mR^2 |
| Solid Sphere | Axis through the center | I = (2/5)mR^2 |
| Thin Circular Ring | Axis through the center | I = mR^2 |
| Solid Disk | Axis through the center | I = (1/2)mR^2 |
| Hollow Disk | Axis through the center | I = (1/2)m(R 1 ^2 + R 2 ^2) |
| T-shaped Object | Axis through the center of mass | I = I 1 + I 2 (sum of individual moments of inertia) |
- represents mass,
- is the perpendicular distance from the axis of rotation to the mass element,
- is the length of the rod,
- and are the sides of the rectangular plate,
- is the radius of the cylinder or sphere,
- and are the inner and outer radius of the hollow cylinder or disk,
- and are the individual moments of inertia for composite objects.
Radius of Gyration
The radius of gyration ( ) is related to the moment of inertia ( ) and the mass ( ) of an object through the following general formula: Here,- is the moment of inertia of the object,
- is the mass of the object, and
- is the radius of gyration.
Relation Between Torque and Moment of Inertia
The relation between torque (τ) and moment of inertia (I) is described by the rotational analog of Newton's second law. The rotational form of Newton's second law relates the torque applied to an object to its resulting angular acceleration. The equation is given by:τ=Iα
Where: τ is the torque applied to the object, I is the moment of inertia of the object, and α is the angular acceleration of the object The relationship indicates that the torque applied to an object is equal to the product of its moment of inertia and angular acceleration. This equation is fundamental in understanding and predicting the rotational motion of objects subjected to torques, such as a force applied at a distance from the axis of rotation.Angular Momentum Definition
Angular momentum ( ) is a measure of the rotational motion of an object around a particular axis. It is a vector quantity that takes into account both the rotational inertia (moment of inertia) of the object and its angular velocity. Angular momentum is conserved in the absence of external torques, similar to the conservation of linear momentum in the absence of external forces.Formula for Angular Momentum
The general formula for angular momentum ( ) is given by:Where:
- is the angular momentum,
- is the moment of inertia of the object, and
- is the angular velocity of the object.
Relation Between Angular Momentum and Torque
The relation between angular momentum (L) and torque (τ) is described by the rotational analog of Newton's second law, which is known as the angular form of Newton's second law. The equation is given by:τ=dt/dL
Here,- τ is the torque applied to the object,
- L is the angular momentum of the object,
- dt/dL represents the time rate of change of angular momentum.
Dynamics of Rigid Bodies Formula FAQs
What is the formula for the dynamics of a rigid body?
What are the dynamics of systems of rigid bodies?
What is the formula for the mechanics of rigid bodies?
How do you calculate rigid body motion?










