Workdone By Constant Force Formula - Definitions,Examples

Definition And Formula Of Workdone By Constant Force

Work done by a constant force is a fundamental concept in physics that describes the energy transferred when a force acts on an object and causes it to move a certain distance. To calculate the work done by a constant force, you can use the following formula:

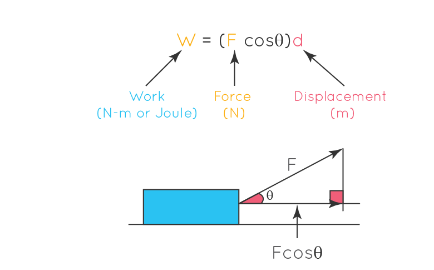
Where:

- W is the work done (measured in joules, J).

- F is the magnitude of the force (measured in newtons, N).

- d is the displacement of the object in the direction of the force (measured in meters, m).

- θ is the angle between the force vector and the direction of displacement (measured in radians).

Also Check - Time of Descent Formula

Here are the key details and steps for calculating the work done by a constant force:

1. Identify the Force: Determine the magnitude and direction of the constant force acting on the object. This force can be applied in various ways, such as pushing, pulling, or lifting.
2. Determine the Displacement: Find the distance and direction over which the object is displaced by the force. The displacement should be measured in the direction of the force.
3. Calculate the Angle \theta: If the force and displacement are not in the same direction, you need to calculate the angle \theta\) between them. This angle is measured in radians and can be found using trigonometry.
4. Plug Values into the Formula: Use the formula W = F dcosθ and substitute the values you have gathered for.
5. Calculate the Work: Perform the calculations to find the work done by the constant force. Ensure that you use consistent units for force (N), displacement (m), and angle \theta.
6. Consider Sign and Interpretation: The sign of the work done can provide information about the nature of the work. Positive work is done when the force and displacement are in the same direction (e.g., lifting an object), while negative work is done when they are in opposite directions (e.g., lowering an object against gravity).
7. Units and Final Answer: Make sure your final answer has the appropriate units (joules, J) and includes the sign to indicate whether the work is done on the object (positive) or by the object (negative).

Also Check - Units, Dimensions & Vector

The work done by a constant force depends on the magnitude of the force, the distance over which the force is applied, and the angle between the force and the direction of displacement. Calculating work is essential in understanding the energy transfer associated with various physical processes and is a fundamental concept in mechanics and physics.

Some Examples Workdone By Constant Force

Here are some examples of calculating the work done by a constant force in different scenarios:

1. Lifting a Weight:

- Scenario: You lift a 10 kg weight vertically upward by applying a constant force of 50 N over a height of 2 meters.

- Work Done W = Force F × Displacement d × cos(θ)

- θ = 0 degrees (since the force is applied vertically upward)

- Work Done W = 50 N × 2 m × cos(0°) = 100 J (joules)

- Interpretation: You did 100 joules of positive work to lift the weight against gravity.

2. Pushing a Car:

- Scenario: You push a car with a constant horizontal force of 500 N for a distance of 10 meters.

- Work Done W = Force F × Displacement d × cos(θ)

- θ = 180 degrees (since the force is applied in the opposite direction of displacement)

- Work Done W = 500 N × 10 m × cos(180°) = -5000 J (joules)

- Interpretation: You did -5000 joules of work, which means you applied a force in the opposite direction of motion, slowing down the car.

3. Pulling an Object Up a Ramp:

- Scenario: You apply a constant force of 200 N to pull a crate up a ramp at an angle of 30 degrees to the horizontal. The displacement along the ramp is 5 meters.

- Work Done W = Force F × Displacement d × cos(θ)

- θ = 30 degrees

- Work Done W = 200 N × 5 m × cos(30°) ≈ 866.03 J

- Interpretation: You did approximately 866.03 joules of work to move the crate up the ramp against gravity.

Also Check - Work, Energy & Power Formula

These examples demonstrate how to calculate work done by a constant force in various situations. The key is to determine the force's direction relative to the displacement and use the formula W = F dcosθ to find the work done, taking into account the angle θ between the force and displacement vectors. The sign of the work indicates the direction of energy transfer.