Physics Wallah

Electromagnetic Induction Formula, Overview, Principle, Equation

Faraday's law, which connects the induced electromotive force (EMF) to the rate of change of magnetic flux across a closed loop or circuit, provides a description of electromagnetic induction.
authorImageGirijesh Singh26 Sept, 2023
Share

Share

Electromagnetic Induction Formula

An electromotive force (EMF) or voltage can be induced in a conductor by a changing magnetic field, according to the fundamental physics concept of electromagnetic induction. Michael Faraday made the initial discovery of this phenomenon in the 19th century, and it is crucial to both electromagnetism and electrical engineering. Electromagnetic induction is responsible for the operation of many devices, including generators, transformers, and even wireless charging systems.

What is Electromagnetic Induction?

An electromotive force (EMF) or voltage is produced in a conductor as a result of a shifting magnetic field, which results in the generation of an electric current. Electromagnetic induction is the term for this phenomenon. This process, which is one of the fundamental ideas in electromagnetics, was discovered and described by Michael Faraday in the 19th century.  Many different technologies and uses, such as wireless charging, transformers, and generators, all depend on electromagnetic induction.

Also Check - Atomic Physics Formula

Electromagnetic Induction Formula

Faraday's law, which connects the induced electromotive force (EMF) to the rate of change of magnetic flux across a closed loop or circuit, provides a description of electromagnetic induction. The formula for electromagnetic induction is given by: ε =-dΦ/dt Where:
  • ε is the induced electromotive force (EMF) in volts (V).
  • dΦ is the change in magnetic flux through the loop or circuit in webers (Wb).
  • dt is the change in time in seconds (s).
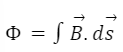This formula quantifies how a changing magnetic field induces an EMF, resulting in the generation of an electric current in a closed loop or circuit. To calculate the magnetic flux through a loop, the following formula is used: 4flux You may determine the induced EMF based on the rate at which the magnetic flux through the loop or circuit changes by combining these formulas. Electromagnetic induction is a fundamental principle with applications ranging from electricity generation to wireless charging and beyond.

Also Check - Current Electricity Formula

Principles of Electromagnetic Induction

The core ideas of electromagnetic induction describe how an electromotive force (EMF) and an electric current can be produced in a conductor by a changing magnetic field. These principles were discovered and formulated by Michael Faraday in the 19th century and are integral to our understanding of electromagnetism. Here are the key principles of electromagnetic induction:
  • Faraday's First Law of Electromagnetic Induction:
A changing magnetic field induces an electromotive force (EMF) in a closed loop or circuit. The rate of change of magnetic flux across the loop directly correlates with the strength of the produced EMF. Mathematically: ε =-dΦ/dt Where:
  • ε  is the induced electromotive force (EMF) in volts (V).
  • dΦ is the change in magnetic flux through the loop or circuit in webers (Wb).
  • dt is the change in time in seconds (s).
  • Faraday's Second Law of Electromagnetic Induction:
The induced EMF creates an electric current in a closed loop or     circuit if a complete path is available for the charges to flow. According to Lenz's Law, the induced current flows in the opposite direction to the change in magnetic flux that created it.
  • Lenz's Law:
According to Lenz's Law, the induced current's direction (and the magnetic field it produces as a result) will always be such that it opposes the change in magnetic flux that caused it. In other words, nature "resists" the change in magnetic flux.
  • Magnetic Flux:
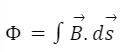Magnetic flux ( ) is a measure of the total magnetic field passing through a surface. Mathematically: 4flux The weber (Wb) is the measure of magnetic flux.
  • Factors Affecting Induced EMF:
The magnitude of the induced EMF depends on factors such as the rate of change of magnetic flux, the number of turns in the loop, and the strength of the magnetic field.
  • Mutual Induction:
Mutual induction occurs when a changing current in one circuit induces an EMF in a neighbouring circuit. This is the principle behind transformers, where primary and secondary coils are wound around a shared magnetic core. If current in primary coil is I , total flux in secondary to proportion to I , i.e N in secondary I . Or N𝛟 in secondary = MI The EMF generated around the secondary due to the current flowing around the primary is directly proportional to the rate at which that current changes.
  • Self-Induction:
Self-induction refers to the phenomenon where a changing current in a circuit induces an EMF in the same circuit, opposing the change in current. This effect is responsible for phenomena like back EMF in inductive components. ε =-Δ (N𝛟 )/Δ t =-Δ (LI)/Δ t =- LΔ I/Δ t The instantaneous EMF is given as ε =- d(N𝛟 )/ dt =- d(LI)/ dt =- LdI/ dt Self inductance of solenoid =μ 0 n 2 π r 2 l These principles of electromagnetic induction have profound implications for the generation of electricity, the operation of transformers, and many other practical applications in electrical engineering and technology. They form the basis for the design and functioning of devices that rely on the conversion of mechanical energy into electrical energy and vice versa.

Also Check - Capacitance Formulas

Applications of Electromagnetic Induction

  • Generators: Electric generators use electromagnetic induction to transform mechanical energy into electrical energy. They are essential for electricity generation in power plants.
  • Transformers: Transformers use electromagnetic induction to modify the alternating current (AC) voltage levels used in power grid transmission and distribution.
  • Induction Cooktops: Induction cooktops use electromagnetic induction to heat cooking vessels directly, providing fast and efficient cooking.
  • Wireless Charging: Electromagnetic induction is the basis for wireless charging technologies used in devices like smartphones and electric toothbrushes.
  • Inductive Sensors: Inductive sensors are frequently employed in industrial automation and automotive systems to detect the presence or absence of metallic objects.
  • Magnetic Resonance Imaging (MRI): MRI machines in medical imaging use electromagnetic induction to create detailed images of the human body's internal structures.
Electromagnetic induction is a fundamental principle that has revolutionised technology and has enabled the development of numerous devices and systems that impact our daily lives.

CBSE Class 10 Sample Paper

Growth of Current in series R - L Circuit

In a series RL circuit (resistor-inductor circuit), the growth of current through the circuit is influenced by the properties of both the resistor and the inductor. Due to the inductor's innate ability to resist fluctuations in current, when a voltage source is attached to the circuit, the current does not immediately reach its final steady-state value. This phenomenon is described by the time constant ( ) of the circuit. Here's how the growth of current occurs in a series RL circuit:
  • Initial Condition ( t = 0 ):
At the instant the voltage source is connected ( t = 0 ), the current in the circuit is initially zero. This is because inductors resist changes in current, and there's no pre-existing current to oppose.
  • Rise of Current ( t > 0 ):
As time progresses, the inductor allows current to flow through the circuit, but its rate of change is limited by the inductance ( L ) of the inductor. The rate of growth of current is inversely proportional to the inductance and resistance ( R ) in the circuit. The equation that describes the growth of current ( I ) in a series RL circuit is given by: I=ε/ R ( 1-e -Rt/ L )
  • Approaching Steady State:
As time increases, the current gradually approaches its final steady-state value (I final = V R ) . The rate of change decreases as the current gets closer to its steady-state value.
  • Steady State ( t → ∞ ):
In the long run (as time goes to infinity), the current in the circuit reaches its steady-state value, which is determined by Ohm's Law (I= V/ R ) . It's important to note that the time constant (τ ) of the RL circuit is given by τ = L/ R . It represents the time it takes for the current to reach approximately 63.2% of its final steady-state value. In summary, in a series RL circuit, the growth of current is gradual due to the inductor's opposition to changes in current. The current rises from zero and approaches its steady-state value according to an exponential growth curve. The time constant (τ ) of the circuit determines the rate at which the current approaches its final value.

Decay of Current in the Circuit Containing Resistor and Inductor

In a circuit containing a resistor and an inductor (RL circuit), the decay of current occurs when the circuit is disconnected from a voltage source, and the current that was initially flowing through the circuit starts to decrease over time. The presence of the inductor in the circuit plays a crucial role in this phenomenon. Here's how the decay of current occurs in an RL circuit after disconnecting the voltage source:
  • Initial Condition ( t = 0 ):
At the instant the voltage source is disconnected ( t = 0 ), the current in the circuit is initially at a certain value, which we'll call I 0 . This is the current that was flowing through the circuit when the voltage source was active.
  • Decay of Current ( t > 0 ):
After the voltage source is disconnected, the inductor opposes the sudden change in current. The magnetic field drops, the inductor resists the drop in current, and its energy is released. The current consequently starts to drop. The equation that describes the decay of current ( I ) in a series RL circuit is given by: I(t)=I 0 .e -Rt / L t ) Where:
  1. I 0 is the initial current when the voltage source is disconnected.
  2. R is the resistance of the circuit.
  3. L is the inductance of the inductor.
  4. t is the time.
  • Rate of Decay:
The rate of decay of current is determined by the resistance ( R ) and the inductance ( L ) of the circuit. A higher resistance or lower inductance will result in a faster decay of current.
  • Complete Decay ( t → ∞ ):
The circuit's current falls to zero as time reaches infinity, signifying that the magnetic field of the inductor has lost all of its stored energy.

Electromagnetic Induction Formula FAQs

What is electromagnetic induction?

A changing magnetic field induces an electromotive force (EMF) or voltage in a conductor, which leads to the creation of an electric current. This process is known as electromagnetic induction.

Who discovered electromagnetic induction?

Electromagnetic induction was discovered and formulated by Michael Faraday in the early 19th century.

What is Faraday's Law of electromagnetic induction?

According to Faraday's Law, the magnetic flux change rate across a closed loop or circuit determines the amount of the induced EMF.

What is Lenz's Law?

According to Lenz's Law, the induced current or magnetic field has a direction that opposes the change in magnetic flux that caused it.

What is the formula for Faraday's Law of electromagnetic induction?

Faraday's Law is represented by the equation: ε=-dΦ/dt , where  is the induced EMF, dΦ is the change in magnetic flux, and dt is the change in time.

How does electromagnetic induction relate to generators?

Generators utilise electromagnetic induction to convert mechanical energy into electrical energy. A rotating coil in a magnetic field generates an EMF, resulting in the production of alternating current (AC).

What are some practical applications of electromagnetic induction?

Electromagnetic induction is used in transformers, electric generators, induction cooktops, wireless charging, inductive sensors, and magnetic resonance imaging (MRI) machines.

What is mutual induction?

hen a circuit's changing current induces an EMF in another circuit next to it, this is known as mutual induction. This principle is employed in transformers.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
07019243492
Check out these Related Articles
BlogImage
SCHOOL PREPARATION
Share
CBSE Compartment Result 2025 OUT, Direct Link to Download Here
Read Full Story
1 Aug 2025, 11:54 pm
BlogImage
CLASS 12 EXAM
Share
CBSE Class 12 Compartment Result 2025 Out, Direct Link To Download Marksheet
Read Full Story
1 Aug 2025, 11:54 pm
BlogImage
ICSETEN
Share
ICSE ISC Improvement Results 2025 Out @cisce.org Check 10th 12th Result
Read Full Story
1 Aug 2025, 05:51 pm
BlogImage
SCHOOL
Share
NCERT Solutions Class 11 chemistry Chapter 2 Structure of atom
Read Full Story
1 Aug 2025, 05:49 pm
BlogImage
CLASS 6 EXAM
Share
NCERT Class 6 Maths Ganita Prakash Chapter 9 Symmetry PDF
Read Full Story
31 Jul 2025, 01:36 pm
BlogImage
CLASS 7 EXAM
Share
NCERT Solutions for Class 7 Maths Ganita Prakash Chapter 3 PDF
Read Full Story
30 Jul 2025, 12:49 pm
BlogImage
CLASS 7 EXAM
Share
NCERT Solutions for Class 7 Science Curiosity Chapter 7
Read Full Story
30 Jul 2025, 05:07 pm
BlogImage
CLASS 7 EXAM
Share
NCERT Solutions for Class 7 Science Curiosity (2025-26 Edition)
Read Full Story
25 Jul 2025, 02:18 pm
BlogImage
CLASS 7 EXAM
Share
NCERT Solutions for Class 7 Science Curiosity Chapter 9 Life Processes in Animals
Read Full Story
11 Jul 2025, 07:00 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.