RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 Mean Median Mode Of Grouped Data
In this article we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 prepared by our experts to help students to prepare better for their examinations.
Ananya Gupta10 Jul, 2024
Share
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1: In RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1, Mean, Median, Mode of Grouped Data, students learn to calculate statistical measures for grouped data sets.
The chapter covers methods to find the mean, median, and mode when data is presented in grouped frequency distributions. It emphasizes understanding the concepts of central tendency and how to interpret them in real-world contexts. Through comprehensive exercises, students practice applying these formulas and interpreting results, enhancing their ability to analyze data effectively.RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 Overview
The RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 have been prepared by experts from Physics Wallah. These solutions help students understand how to find the mean, median, and mode for grouped data. They are designed with clear explanations and examples to make learning easier. By using these solutions, students can improve their understanding of statistics and feel more confident solving problems involving data analysis.RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF
The PDF link for RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 is available below. This PDF provides detailed solutions for calculating mean, median, and mode of grouped data, helping students grasp these statistical concepts effectively. By accessing this PDF, students can enhance their understanding and practice solving problems related to data analysis in a structured manner.RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Mean Median Mode Of Grouped Data Cumulative Frequency Graph And Ojive Exercise 9.1
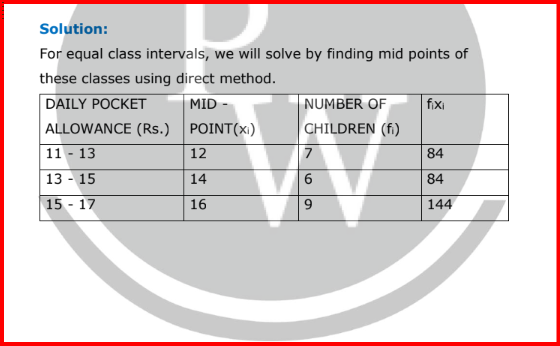
Here we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 for the ease of students so that they can prepare better for their exams.Q. If the mean of 5 observations x , x + 2 , x + 4 , x + 6 and x + 8 is 11 , find the value of x .
Q. If the mean of 25 observations is 27 and each observation is decreased by 7, what will be the new mean?
For equal class intervals, we will solve by finding mid points of these classes using direct method.
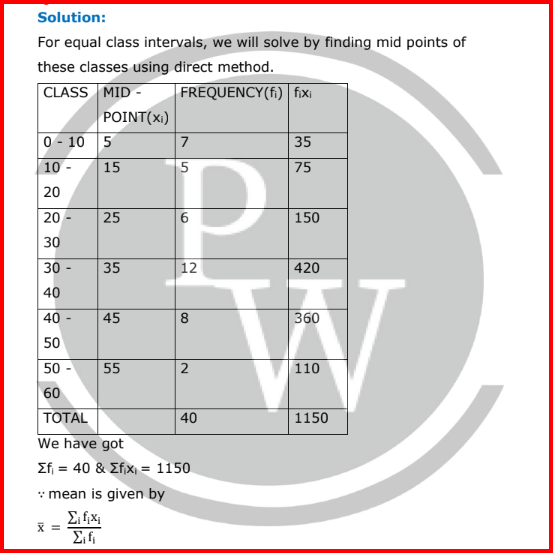⇒ x̅ =
1150
40
⇒ x̅ = 28.75
Thus, mean is 28.75
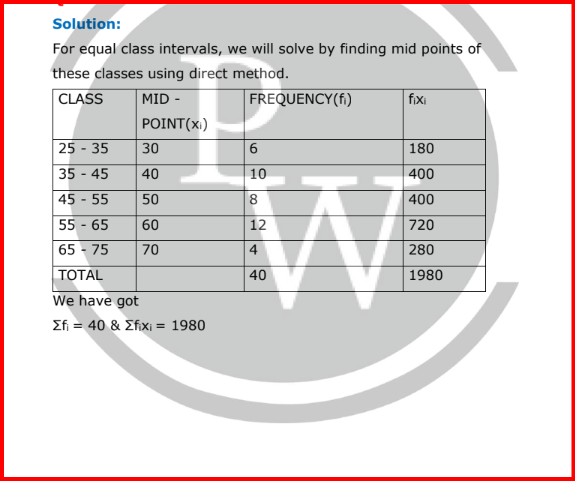∵ mean is given by
x̅ =
∑ fi ixi
∑ fi i
⇒ x̅ =
1980
40
⇒ x̅ = 49.5
Thus, mean is 49.5
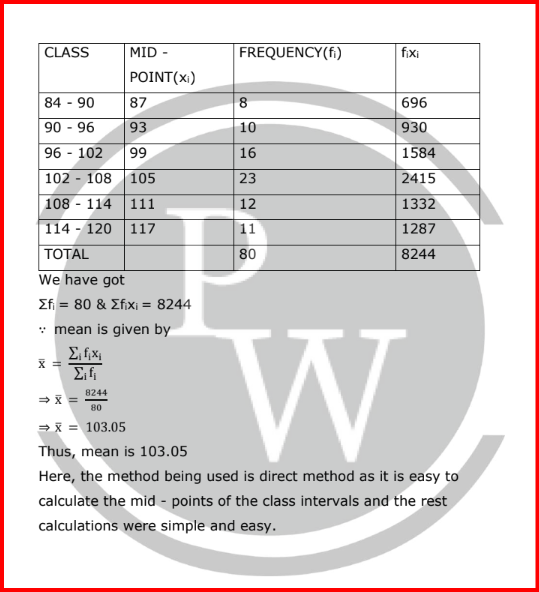
We have got
Σfi = 50 & Σfixi = 13200
∵ mean is given by
x̅ =
∑ fi ixi
∑ fi i
⇒ x̅ =
13200
50
⇒ x̅ = 264
Thus, mean is 264
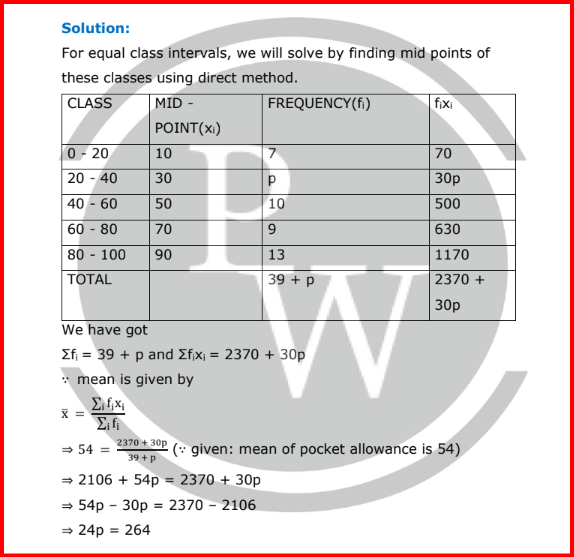
For equal class intervals, we will solve by finding mid points of these classes using direct method.
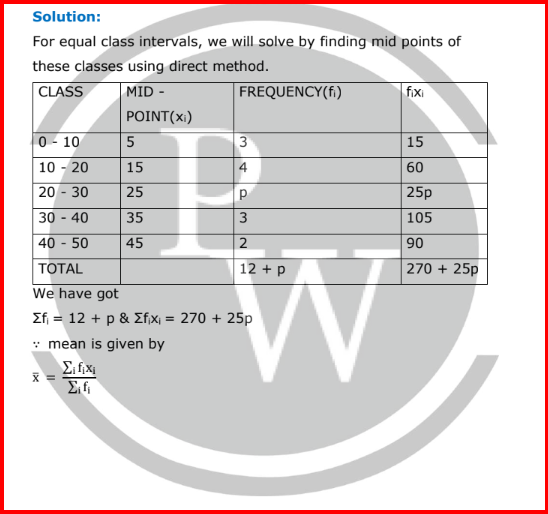⇒ 24 =
270 + 25p
12 + p
⇒ 288 + 24p = 270 + 25p
⇒ 25p – 24p = 288 – 270
⇒ p = 18
Thus, p is 18
⇒ p = 11
Thus, p is 11.
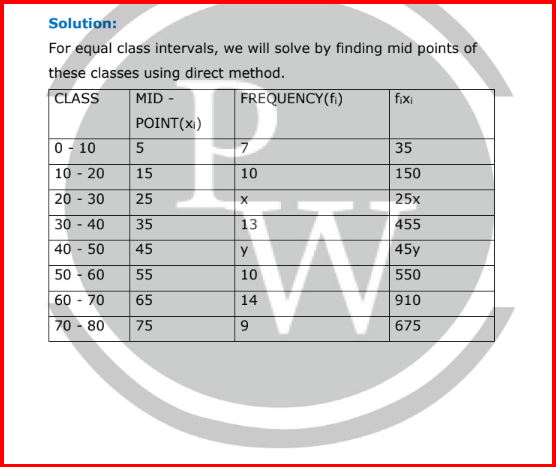
⇒ x = 12
Substitute x = 12 in equation (ii),
12 + y = 37
⇒ y = 37 – 12
⇒ y = 25
Thus, x = 12 and y = 25.
Benefits of RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1
- Clarity in Concepts: The solutions provide clear explanations and step-by-step methods for calculating mean, median, and mode of grouped data helping students understand the concepts better.
- Practice: Students get ample practice with various types of problems, enhancing their proficiency in applying statistical measures to real-world data sets.
- Structured Learning: The solutions are organized systematically making it easier for students to follow and apply the methods taught in the chapter.
- Improved Problem-Solving Skills: By using these solutions, students can develop stronger problem-solving skills, crucial for tackling mathematical problems in exams and beyond.
- Confidence Building: Through thorough practice and understanding gained from these solutions, students gain confidence in their ability to handle statistical calculations effectively.
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.1 FAQs
What is meant by grouped data?
Grouped data refers to data that has been categorized into intervals or groups rather than individual values. This is often done to simplify large sets of data for analysis.
Why are mean, median, and mode important for grouped data?
These measures of central tendency help summarize the data and provide insights into its typical or central values. Mean gives an average value, median represents the middle value, and mode shows the most frequently occurring value in the grouped data.
What does the mode indicate in grouped data?
The mode represents the value or class interval that appears most frequently in the data. It helps identify the most common characteristic or value within the data set.
When should you use mean, median, or mode for grouped data?
Use mean when the data is normally distributed and you need an average value.
Use median when the data set is skewed or contains outliers, as it is less affected by extreme values.
Use mode when you need to identify the most common value or category in the data.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App