RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2
In this article we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 prepared by our experts to help students to prepare better for their examinations.
Ananya Gupta11 Jul, 2024
Share
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2: RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 provide detailed explanations to help students solve problems related to cumulative frequency distribution and drawing ogive curves.
By working through these exercises, students can improve their ability to create cumulative frequency tables and graphs, which are important for analyzing data. These solutions are a great resource for students to practice and prepare for their math exams effectively.RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 Overview
The RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 have been prepared by subject experts from Physics Wallah. These solutions provide clear and detailed explanations for solving problems related to cumulative frequency distribution and drawing ogive curves. By practicing these exercises students can improve their skills and confidence making these solutions a valuable resource for exam preparation.RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 PDF
The PDF link for RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 is available below. This PDF provides detailed solutions to problems involving cumulative frequency distribution and ogive curves, prepared by subject experts from Physics Wallah.
By accessing this PDF, students can practice and improve their skills in data representation and analysis making it a valuable resource for their exam preparation.
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 PDF
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Mean Median Mode Of Grouped Data Cumulative Frequency Graph And Ogive Exercise 9.2
Here we have provided RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 for the ease of students so that they can prepare better for their exams.
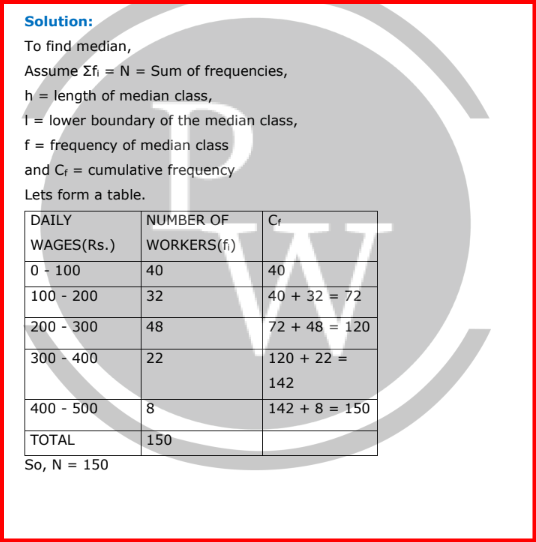⇒ N/2 = 150/2 = 75
The cumulative frequency just greater than (N/2 = ) 75 is 120, so
the corresponding median class is 200 - 300 and accordingly we
get Cf = 72(cumulative frequency before the median class).
Now, since median class is 200 - 300.
∴ l = 200, h = 100, f = 48, N/2 = 75 and Cf = 72
Median is given by,
Median = l + (
N
2
− Cf
f
) × h
⇒ Median = 200 + (
75−72
48 ) × 100
= 200 + 6.25
= 206.25
Thus, median wage is Rs. 206.25.
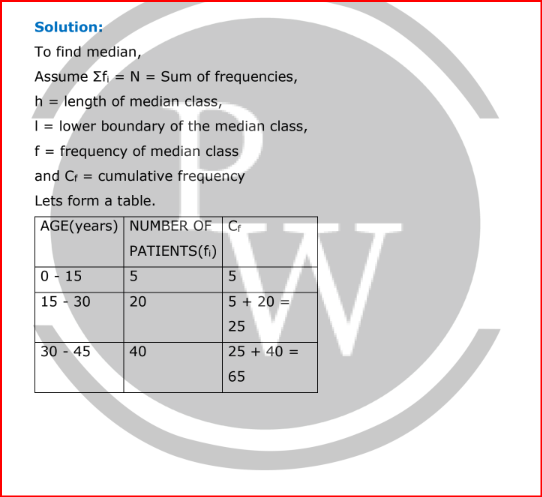
To find median, Assume
Σfi = N = Sum of frequencies,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
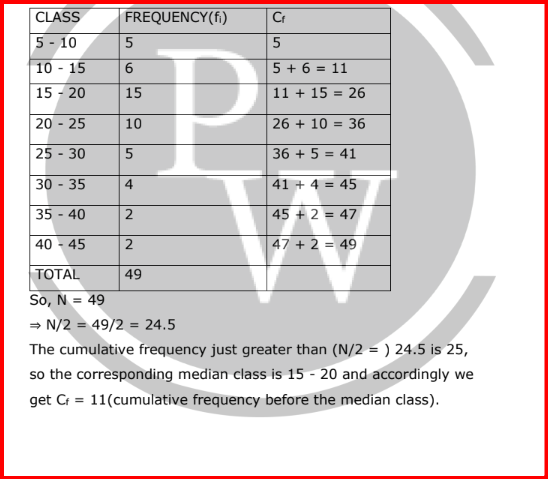Now, since median class is 15 - 20.
∴ l = 15, h = 5, f = 15, N/2 = 24.5 and Cf = 11
Median is given by,
Median = l + (
N
2
− Cf
f
) × h
⇒ Median = 15 + (
24.5−11
15 ) × 5
= 15 + 4.5
= 19.5
Thus, median is 19.5.
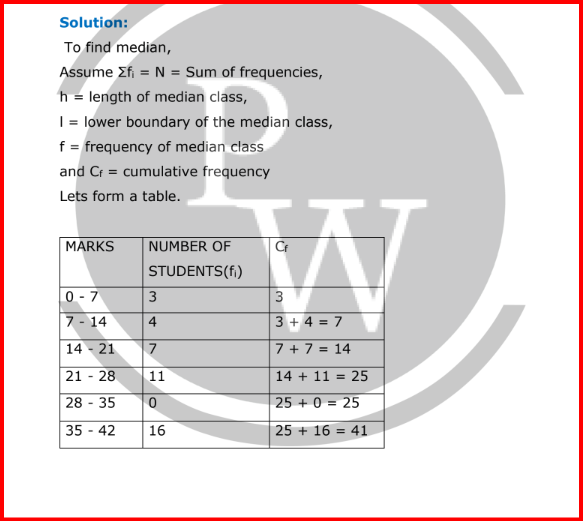
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table.
∴ l = 125, h = 20, f = 20, N/2 = 33.5 and Cf = 22
Median is given by,
Median = l + (
N
2
− Cf
f
) × h
⇒ Median = 125 + (
33.5−22
20 ) × 20
= 125 + 11.5
= 136.5
Thus, median is 136.5.
To find median, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
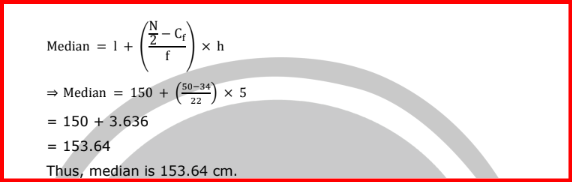
Median(given) = 24, Assume
Σfi = N = Sum of frequencies,
h = length of median class,
l = lower boundary of the median class,
f = frequency of median class
and Cf = cumulative frequency
Lets form a table, where x is the unknown frequency.
⇒ (4)(2x) = 10x – 50
⇒ 8x = 10x – 50
⇒ 10x – 8x = 50
⇒ 2x = 50
⇒ x = 25
Thus, the unknown frequency is 25.
Benefits of RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2
- Clear Explanations: The solutions provide step-by-step explanations making it easier for students to understand how to solve problems related to cumulative frequency distribution and ogive curves.
- Expert Guidance: Prepared by subject experts from Physics Wallah, the solutions ensure accuracy and reliability, giving students confidence in their learning.
- Enhanced Understanding: By practicing these solutions, students can deepen their understanding of data representation and analysis which are important concepts in statistics.
- Improved Graphing Skills: The solutions help students learn how to create and interpret cumulative frequency tables and ogive curves improving their graphing skills.
- Boosts Confidence: With clear guidance and thorough practice students can build their confidence in tackling similar problems in exams and real-life situations.
RS Aggarwal Solutions for Class 10 Maths Chapter 9 Exercise 9.2 FAQs
Why are mean, median, and mode important in statistics?
Mean, median, and mode are measures of central tendency that summarize a data set by identifying its central value. They are useful for understanding the overall distribution and trends within the data.
When should you use mean, median, or mode?
Use the mean for data that is symmetrically distributed without outliers.
Use the median for data that is skewed or has outliers, as it is less affected by extreme values.
Use the mode when you need to identify the most frequently occurring value, especially for categorical data.
How do you identify the modal class?
The modal class is the class interval with the highest frequency.
What is the mode of grouped data?
The mode is the value that occurs most frequently in the data set.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App