We have already studied that the square of a number is the product of the number with the number itself. For example a given number is x, the square of x is (x x x), denoted by x
2
.
e.g. (9)
2
= 9 x 9 = 81
(5)
2
= 5x 5 = 25
(10)
2
= 10x 10 = 100
(1.2)
2
= 1.2x 1.2 = 1.44
Perfect Squares or Square Numbers
A natural number is called a perfect square or a square number if it is the square of some natural numbers. It is always expressible as the product of equal factors.
e.g.
49 = 7x 7 = 7
2
144 =2 x 2 x 2 x 2 x 3 x 3 = 12x 12 = 12
2
225 = 5x 5x 3 x 3 = 15x 15 = 15
2
1000= 2 x 2 x 5x 5 = 10x 10 = 10
2
Example.
Show that 500 is not a perfect square.
Ans.
Resolving 500 in to prime factors, we get
500 =
2
x
2
x 5x
5
x
5
Making pairs of equal factors, we find that 5 is unpaired
Hence 500 is not a perfect square.
Properties of Perfect Squares
Example 1.
A number ending in 2, 3, 7 or 8 is never a perfect square
e.g.
62,103,113,148 ,237,107.
Example
2.
A number ending in an odd number of zeros is never a perfect square.
e.g.
10,3000 , 13000, 120, 100000.
Example
3.
The square of a even number is always even.
e.g.
12
2
= 144, 16
2
= 256 30
2
= 900 etc.
Example
4.
The square of an odd number is always odd.
E.g.
5
2
= 25, 7
2
= 49, 13
2
=169, 11
2
= 121 etc.
Example
5.
The square of a proper fraction is smaller than the fraction.
e.g.
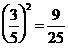and
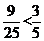since 9x 5 < 25x 3.
Example
6.
For every natural number n we have
(n + 1)
2
– n
2
= (n + 1 + n) (n + 1 – n) = {(n + 1) + n}
{(25)
2
– (24)
2
} = (25 + 24) = 49
{(70)
2
– (69)
2
} = (70 + 69) = 139
Example 7.
For every natural number n, we have sum of the first n odd natural numbers = n
2
E.g.
{1+3+5+7+9+11+13}=Sum of first 6 odd numbers=6
2
=36
{1+3+5+7+9+11+13+15+17+19}}=Sum of first 10 odd numbers=10
2
=100
Pythagorus Triplets
A triplet (m, n, p) of three natural number. m, n and p is called a Pythagoras triplet of m
2
+ n
2
= p
2
E.g. (3, 4, 5) (5, 12, 13), (8, 15, 17), etc.
Example 8.
For every natural number m greater than 1, (2m, m
2
– 1, m
2
+ 1) is a Pythagoras triplet.
Find the Pythagoras triplet where smallest number is 10.
Ans.
For every natural number m > 1, (2m, m
2
– 1, m
2
+ 1) is a Pythagoras triplet
For every natural number m > 1, (2m, m
2
– 1, m
2
+ 1) is a Pythagoras triplet.
Put 2m = 12 m = 6
m
2
– 1 = 35
m
2
+ 1 = 36
triplet (12, 35, 37)
Some Interesting Patterns of Square Numbers
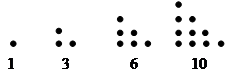
Sum of first two is 4
Sum of second and third is 9
Sum of third and forth is 16… and so on
Thus n
th
triangular number is given by
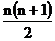
Part
I.
There are 2n non-perfect square numbers between two consecutive square number n
2
and (n + 1)
2
.
e.g. Between the number 5
2
and4
2
.Total 8 numbers are between these two numbers.
Between the number 50
2
and49
2
.Total 98 numbers are between these two numbers.
Part
II.
The sum of first n odd natural numbers in n
2
n = 1 1 = 1 = 1
2
n = 2 1 + 3 = 4 = 2
2
n = 3 1 + 3 + 5 = 9 = 3
2
n = 4 1 + 3 + 5 + 7 = 16 = 4
2
n = 5 1 + 3 + 5 + 7+9 = 25 = 5
2
n=10 1+3+5+7+9+11+13+15+17+19 =10
2
Part
III.
If 1 is added to the product of two consecutive odd natural numbers, it is equal to the square of the only even natural number between them.
In general
(2n – 1) x (2n + 1) + 1 = 4n
2
= (2n)
2
this pattern is very useful to find the result
1 x 3 + 1 = 4 = 2
2
3 x 5 + 1 = 16 = 4
2
5 x 7 + 1 = 36 = 6
2
7 x 9 + 1 = 64 = 8
2
etc.
In reverse way we can factorize (2n)
2
-1 in two factors as (2n – 1) x (2n + 1)
Part I
V
. If 1 is added to the product of two consecutive even natural numbers, it is equal to the square of the only odd natural number between them.
In general
2n (2n + 2) + 1 = 4n
2
+ 4n + 1 = (2n + 1)
2
E.g
2 x 4 + 1 = 9 = 3
2
4 x 6 + 1 = 25 = 5
2
6 x 8 + 1 = 49 = 7
2
8 x 10 + 1 = 81 = 9
2
10x 12 + 1 = 121 = 11
2
12x 14 + 1 = 169 = 13
2
and so on ………………
In reverse way we can factorize (2n + 1)
2
-1 in two factors as 2n (2n + 2)= 4n(n+1)
Part
V.
Squares of natural numbers having all digits 1 follow the following pattern.
11
2
= 121
111
2
= 12321
1111
2
= 1234321
11111
2
= 123454321
111111
2
= 12345654321
and so on …………
we can use this in many ways as
22
2
= 4 x121=484
333
2
= 9 x12321 =110889
222222
2
= 4 x12345654321= 49382737284
Using suitable patterns, compute the following
(i)
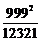(ii)
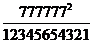
Ans.
We have the following pattern
11
2
= 121
111
2
= 12321
1111
2
= 1234321
11111
2
= 123454321
111111
2
= 12345654321
(i)
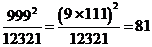= 81.
(ii)
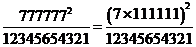= 49.
Part
VI.
Observe the following pattern
7
2
= 49
67
2
= 4489
667
2
= 444889
6667
2
= 4444889
66667
2
= 44444889
and so on
Some Short–Cuts to Find Squares
Three column method
– This method is based upon an old Indian method of multiplying two numbers. It is convenient for finding squares of two digit numbers only. This method uses the identity (a + b)
2
= a
2
+ 2ab + b
2
Step I :
Make three columns and write the value of a
2
, 2 x a x b and b
2
respectively in these columns as follows:
As an illustration let us take ab = 34 = 3x10+4
a = 3 and b = 4
|
Column-I
|
Column-II
|
Column-III
|
|
a
2
9
|
2 x a x b
24
|
b
2
16
2222
|
Step II :
Undertake the units digit of b
2
( in column III) and add its tens digit, if any, to 2 x a x b (n column II)
|
Column-I
|
Column-II
|
Column-III
|
|
9
|
24
+1
25
|
1
6
2222
|
Step III :
Undertake the units digit in column II and add the number forward by tens and other digit, if any to a
2
in column II.
|
Column-I
a
2
|
Column-II
2 x a x b
|
Column-III
b
2
|
|
9
+2
|
24
+1
|
1
6
2222
|
|
11
|
25
|
|
Step IV :
Under the number in column I
|
Column-I
a
2
|
Column-II
2 x a x b
|
Column-III
b
2
|
|
9
+2
11
|
24
+1
2
5
|
1
6
2222
|
|
11
|
5
|
6
|
Step V:
Write the understual digits at the bottom of each column to obtain the square of the given number.
In this case, we have 34
2
= 1156.
Some Particular Methods
Rule1:
The square of a number of the form
a 5
(where a is tens digit and 5 is units digit) is the number which each in 25 and has the number a(a + 1) before 25.
Example:
Find the squares of the following numbers
-
45
-
95
-
85
Ans.
1. Here we have
a = 4=> a(a + 1) = 4× 5 = 20
(45)
2
= 2025
2. Here, we have
a = 9 => a(a + 1) = 9 x 10 = 90
\95
2
= 9025.
3. Here, we have
a = 8=> a(a + 1) = 8x 9 = 72
75
2
= 7225.
Rule 2 :
The square of a number of the form ( 5x 10 + a ) (where a is units digit and 5 is ten digit) is equal to
(25 + a) x 100 + a
2
(5 a)
2
= (25 + a) x 100 + a
2
Example
:
Find the squares of the following numbers
-
51
-
53
-
56
Ans.
1. Here, we have
a = 1
(51)
2
= (25 + 1) x 100 + 1
2
= 2600 + 01 = 2601.
2. Here, we have
a = 3
(53)
2
= (25 + 3) x 100 + 3
2
= 2800 + 09
= 2809
3. Here, we have
a = 6
(56)
2
= (25 + 6) x 100 + 6
2
= 3100 + 36 = 3136.
Rule 3 :
The square of a three digit number (5x 100+ ax10 +b) (where a,b are integers from 0 to 9.
(5x 100+ ax10 +b)
2
= (250 + ab) x 1000 + (ax10 + b)
2
Example:
Find the squares of the following numbers
-
516
-
513
-
504
Ans.
1. Given number is 516
a = 1, b= 6
(516)
2
= (250 + 16) x 1000 + (16)
2
= 266000 + 256
= 266256.
2. Here, we have
a = 1, b = 3
(513)
2
= (250 + 13) x 1000 + (13)
2
= 263000 + 169
= 263169.
3. Here, we have
a = 1, b = 3
(504)
2
= (250 + 04) x 1000 + (04)
2
= 254000 + 16
= 254016.
Rule 4 :
The square of a number abc…..5 (i.e., a number having 5 at units place is obtained by affixing 25 to we right of the number n(n + 1), where n = abc….
Example:
Find the square of the following numbers
-
225
-
265
-
1235
Ans.
1. 225
Here n = 22
n(n + 1) = 22 x 23
= 506
Hence 225
2
= 50625
2. 265
Here n = 26
n(n + 1) =26x 27
= 702
Hence 225
2
= 70225
3. 1235
Here n = 123
(n + 1) = 123 x 124
= 15252
Hence 1235
2
= 1525225
Related Pages
-
Class 7 Maths Worksheet
-
Class 7 Maths Notes
