
Trigonometric
Trigonometry of Class 10
Trigonometric formulas for class 10 are given here for students. Trigonometry studies relationships between angles, lengths, and heights of triangles. It includes ratios, functions, identities, and formulas for solving problems based on them, especially for right triangles. Applications of trigonometry are also found in engineering, astronomy, physics, and architectural design. This chapter is very important because it covers many topics such as linear algebra, calculus, and statistics.
Trigonometry Formula list for class 10
All the important trigonometry formulas introduced to students in Class 10 are available at Physics Wallah. Students can learn these formulas anytime from Physics Wallah and solve trigonometry-related problems.
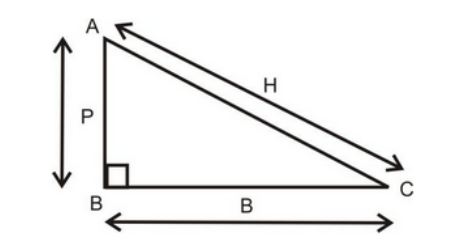
Class 10 trigonometric formulas for ratios are majorly based on the three sides of a right-angled triangle, such as the adjacent side or perpendicular, base, and hypotenuse (See the given figure). Now, applying Pythagoras theorem for the given right-angled triangle,
(Perpendicular) 2 + (Base) 2 = (Hypotenuse) 2
(P) 2 + (B) 2 = (H) 2
Now, let us check the formulas based on trigonometric ratios (sine, cosine, tangent, secant, cosecant, and cotangent)
Basic Trigonometric formulas
| S.no | Property | Mathematical value |
| 1 | sin A | Perpendicular/Hypotenuse |
| 2 | cos A | Base/Hypotenuse |
| 3 | tan A | Perpendicular/Base |
| 4 | cot A | Base/Perpendicular |
| 5 | cosec A | Hypotenuse/Perpendicular |
| 6 | sec A | Hypotenuse/Base |
Relation Between Trigonometric Ratios
| S.no | Identity | Relation |
| 1 | tan A | sin A/cos A |
| 2 | cot A | cos A/sin A |
| 3 | cosec A | 1/sin A |
| 4 | sec A | 1/cos A |
Trigonometric Sign Functions
- sin (-θ) = − sin θ
- cos (−θ) = cos θ
- tan (−θ) = − tan θ
- cosec (−θ) = − cosec θ
- sec (−θ) = sec θ
- cot (−θ) = − cot θ
Trigonometric Identities
- sin 2 A + cos 2 A = 1
- tan 2 A + 1 = sec 2 A
- cot 2 A + 1 = cosec 2 A
Periodic Identities
- sin(2nπ + θ ) = sin θ
- cos(2nπ + θ ) = cos θ
- tan(2nπ + θ ) = tan θ
- cot(2nπ + θ ) = cot θ
- sec(2nπ + θ ) = sec θ
- cosec(2nπ + θ ) = cosec θ
Complementary Ratios
Quadrant I
- sin(π/2 − θ) = cos θ
- cos(π/2 − θ) = sin θ
- tan(π/2 − θ) = cot θ
- cot(π/2 − θ) = tan θ
- sec(π/2 − θ) = cosec θ
- cosec(π/2 − θ) = sec θ
Quadrant II
- sin(π − θ) = sin θ
- cos(π − θ) = -cos θ
- tan(π − θ) = -tan θ
- cot(π − θ) = – cot θ
- sec(π − θ) = -sec θ
- cosec(π − θ) = cosec θ
Quadrant III
- sin(π + θ) = – sin θ
- cos(π + θ) = – cos θ
- tan(π + θ) = tan θ
- cot(π + θ) = cot θ
- sec(π + θ) = -sec θ
- cosec(π + θ) = -cosec θ
Quadrant IV
- sin(2π − θ) = – sin θ
- cos(2π − θ) = cos θ
- tan(2π − θ) = – tan θ
- cot(2π − θ) = – cot θ
- sec(2π − θ) = sec θ
- cosec(2π − θ) = -cosec θ
Sum and Difference of Two Angles
- sin (A + B) = sin A cos B + cos A sin B
- sin (A − B) = sin A cos B – cos A sin B
- cos (A + B) = cos A cos B – sin A sin B
- cos (A – B) = cos A cos B + sin A sin B
- tan(A + B) = [(tan A + tan B) / (1 – tan A tan B)]
- tan(A – B) = [(tan A – tan B) / (1 + tan A tan B)]
Double Angle Formulas
- sin 2A = 2 sin A cos A = [2 tan A /(1 + tan 2 A)]
- cos 2A = cos 2 A – sin 2 A = 1 – 2 sin 2 A = 2 cos 2 A – 1 = [(1 – tan 2 A)/(1 + tan 2 A)]
- tan 2A = (2 tan A)/(1 – tan 2 A)
Triple Angle Formulas
- sin 3A = 3 sinA – 4 sin 3 A
- cos 3A = 4 cos 3 A – 3 cos A
- tan 3A = [3 tan A – tan 3 A] / [1 − 3 tan 2 A]
Solved Examples
Q1. If cot Q = tan P then prove that P + Q = 90°.
Ans. Given,
tan P = cot Q
As we know, cot(90° – A) = Tan A.
So, cot Q = cot(90° – P)
Therefore, Q = 90° – P
And
P + Q = 90°
Hence proved.
Q2. Evaluate cos 55° sin 35° + cos 35° sin 55°.
Ans. Given expression:
cos 55° sin 35° + cos 35° sin 55°
The above equation is in the form sin A cos B + cos A sin B.
Now, using sin(A + B) = sin A cos B + cos A sin B, we get;
cos 55° sin 35° + cos 35° sin 55° = sin(35° + 55°) = sin 90° = 1
Q3. If sin A = 3/5, then find the value of cos A and cot A
Ans . Sin A = 3/5
Now, sin 2 A + cos 2 A = 1
cos 2 A = 1- (3/5) 2
= (25 - 9) / 25
= 16 / 25
cos A = 4/5
Also, cot A = cosA / sinA
= (4/5)(3/5)
= 4/3
Frequently Asked Question (FAQs)
Q1. What are the Pythagorean identities of trigonometry?
Ans. The three trigonometry identities are known as the Pythagorean identities of trigonometry.
- sin 2 A + cos 2 A = 1
- tan 2 A + 1 = sec 2 A
- cot 2 A + 1 = cosec 2 A
Q2. How do you introduce trigonometry to class 10?
Ans. Following are the steps to introduce trigonometry:
- Firstly, measure the lengths of the sides of sets of right-angled triangles and then find the ratio of sides.
- Find the relationship between the ratios and the angle size.
- Always use calculators or tables to find the sine, cosine, and tangent of angles.
Q3. Who is the father of trigonometry in India?
Ans. The first trigonometric table was compiled by Hipparchus, who is now known as "the father of trigonometry."
Q4. What are the six ratios of trigonometry?
Ans. The six ratios of trigonometric are sine, cosine, tangent, cosecant, secant and cotangent.
Q5. What are the two types of trigonometry?
Ans. The two types of trigonometry are Plane Trigonometry and Spherical Trigonometry.









