LAW OF CONSERVATION OF ENERGY
According to law of conservation of energy whenever energy gets transformed, the total energy remains unchanged. Energy can be transformed from one form to another.
i.e. energy can neither be created nor destroyed. The total energy before and after the transformation remains the same.
The law of conservation of energy is valid in all situations and for all kinds of transformations.
LAW OF CONSERVATION OF MECHANICAL ENERGY:
If conservation forces are acting on a body or on a system, then the sum of kinetic energy and potential energy (mechanical energy) of the body or of the system will be conserved. If the presence of conservative forces, if the kinetic energy is increased by an amount of
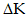then the potential energy of the body will decrease by the same amount i.e.
.
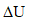So,
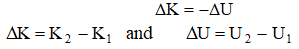
So, K
2
– K
1
= – (U
2
– U
1
)
K
2
– K
1
= – U
2
+ U
1
K
2
+ U
2
= K
1
+ U
1
Final mechanical energy = Initial mechanical energy.
So in the presence of conservative forces the sum of Kinetic energy and the potential energy of a body will be conserved.
MECHANICAL ENERGY OF A FREELY FALLING BODY:
Let a body of mass m is at rest at a height h from the earth’s surface, when it starts falling, after a distance x (point B) its velocity becomes v and at earth’s surface its velocity is v’
At point A :
E
A
= Kinetic energy + Potential energy
E
A
= m(o)
2
+ mgh
E
A
= mgh .... (i)
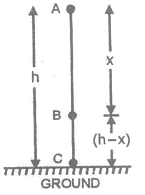
At point B :
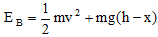….(ii)
From third equation of motion at points A and B
v
2
= u
2
+ 2gx
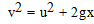u = 0
v
2
= 2gx
On putting the value of v
2
in equation (ii)
EB m(2gx) + mgh - mgx
EB = mgx + mgh - mgx
EB mgh ..... (iii)
At point C :
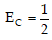m (v’)
2
+ mg × o.
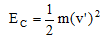……(iv)
From third equation of motion at points A and C.
(v’)
2
= u
2
+ 2gh
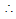u = 0
So, (v’)
2
= 2gh
On putting the value of (v’)
2
in equation (iv)
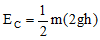
or EC = mgh ....(v)
From equation (i), (ii) and (v)
EA = EB = EC
Hence, the mechanical energy of a freely falling body will be constant.
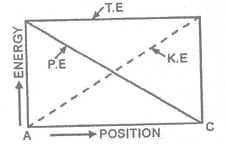
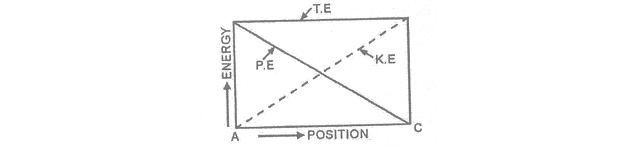
i.e. Total energy of the body during free fall, remains constant at all positions. The form of energy, however keeps on changing. AT point A, energy is entirely potential energy and at point C, it is entirely kinetic energy In between A and C, energy is partially potential and practically kinetic. This variation of energy is shown in figure. Total mechanical energy stays constant (mgh) throughout. Thus is an isolated system, where only conservation forces cause energy changes, the kinetic energy and potential energy can change, but the mechanical energy of the system (which is sum of kinetic energy and potential energy) cannot change. We can, therefore, equate the sum of kinetic energy and potential energy at one instant to the sum of kinetic energy and potential energy at another instant without considering intermediate state. This law has been found to be valid in every situation. No violation, whatsoever, of this law has ever been observed.
Question10.
A body of mass 20 kg is kept at a height 20 m from the ground, when it is released after sometime its kinetic energy becomes 500 J. What will be the potential energy of the body at the instant?
Solution:
At a height of 10 m. The mechanical energy of the body,
E = Kinetic energy + potential energy
E = m (o)
2
+ mgh (
initial velocity of the body is zero)
E = 20 × 10 × 20 = 4000 J.
After sometime the kinetic energy is 500 J. Suppose at that instant potential energy is U, then by the law of conservation of mechanical energy.
E = 450 + U
4000 = 500 + U
or U = 4000 - 500
U = 3500 J.
CONSERVATION OF ENERGY IN A SIMPLE PENDULUM
A swinging simple pendulum is an example of conservation of energy.
-
A simple pendulum consists of a small metal ball or bob suspended by a long thread from a rigid support, such that the bob is free to swing back and forth when displaced.
-
Initially, the simple pendulum is at rest with its bob in the centre position or mean position.
-
When the pendulum bob is pulled to one side i.e. to position B and then released the bob starts swinging between positions B and C.
-
When the pendulum bob is at position B, it has only potential energy and no kinetic energy
-
As the bob moves down from position B to position A, its potential energy goes on decreasing but its kinetic energy goes on increasing.
-
When the bob reaches the centre position A, it has only kinetic energy but no potential energy.
-
As the bob goes from position A towards position C, its kinetic energy goes on decreasing but its potential energy goes on increasing.
-
On reaching the extreme position C, the bob stops for a very small instant of time. So at position C the bob has only potential energy but no kinetic energy.
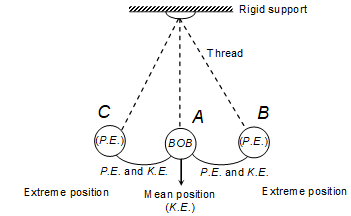
Conclusion:
At the extreme positions B and C, all the energy of pendulum bob is potential and at the centre position A, all the energy of the bob is kinetic.
At all the other intermediate positions, the energy of pendulum bob is partly potential and partly kinetic.
But the total energy of the swinging pendulum at any instant of time remains the same or conserved.
Related Topics
