Cofactor Formula with Solved Example

Before delving into the Cofactor formula, it's important to understand its practical application. The inverse of a matrix plays a crucial role in solving systems of equations. Specifically, the inverse of a matrix is derived by dividing its adjoint by its determinant. The adjoint of the matrix can be obtained by transposing the cofactor matrix, which is created by replacing the elements of the original matrix with their respective cofactors. These cofactors are computed using the cofactor formula. So, let's now explore the cofactor formula in detail, accompanied by some solved examples.

What Is Cofactor Formula?

The cofactor, denoted as C _ij , associated with an element a _ij in a square matrix of order n × n, is calculated by multiplying its minor, M _ij by (-1) ^i+j . To compute the minor M _ij of the element a _ij we find the determinant of the matrix obtained by excluding the i ^th row and j ^th column from the original matrix. In other words:

Cofactor of an element a _ij is given by:

C _ij = (-1) ^i+j * M _ij

Where:

M _ij represents the minor of a _ij , which is equal to the determinant of the matrix obtained by removing the i ^th row and j ^th column.

1. Minor of a _ij is, M _ij = Determinant of the matrix obtained by removing i ^th row and j ^th
2. Cofactor of a _ii is, C _ij = (-1) ^i+j M _ij

Certainly, here are some important notes:

(i). To find the determinant of a 2 × 2 matrix [a, b, c, d], you can use the formula:

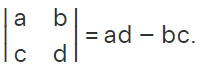
(ii). It's crucial to note that the cofactor of an element can take positive, negative, or zero values. The sign of the cofactor depends on the position of the element within the matrix, specifically determined by (-1) ^i+j where i and j are the row and column indices of the element.

Also Check – Logarithm Formula

Examples Using Cofactor Formula

Example: Find the Co-factor Formula for

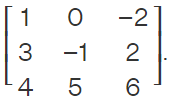
Ans: Before finding the cofactor of 0, we will first find its minor.

Minor of 0 = 3(6) - 4(2) = 18 - 8 = 10.

0 is present in 1 ^st row and 2 ^nd column. So

The cofactor of 0 = (-1) ^{1 + 2} (10) = -10

Answer: The cofactor of 0 is -10.