Physics Wallah

Logarithm Formula: Rules, Explanation, Solved Examples

Logarithms are mathematical functions used to solve problems involving exponential growth and decay, and they have applications in various fields such as mathematics, science, engineering, and finance. Logarithms are essentially the inverse operations of exponentiation.
authorImageAnchal Singh9 Sept, 2023
Share

Share

Logarithm Formula: Rules, Explanation, Solved Examples

Before delving into Logarithm Formula , let's refresh our understanding of logarithms. Logarithms provide an alternative notation for expressing exponents. When conventional exponentiation isn't suitable for problem-solving, logarithms come into play. Various logarithmic formulas stem from the laws governing exponents. We'll familiarize ourselves with these formulas through a selection of solved examples.

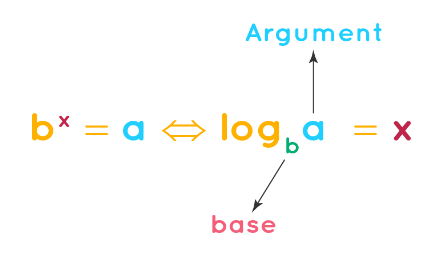
Logarithmic Formulas

What Are Log Formulas?

Prior to delving into the study of logarithm formula, it's beneficial to review certain concepts. Logarithms can be classified into two types: common logarithms, denoted as "log" with a default base of 10 if unspecified, and natural logarithms, denoted as "ln" with a constant base of "e." The subsequent logarithmic formulas are presented using common logarithms, but they hold true for natural logarithms as well. Here are the frequently employed logarithmic expressions:

formulas .

  • log b 1 = 0
  • log b b = 1
  • log b (xy) = log b x + log b y
  • log b (x / y) = log b x - log b y
  • log b a x = x log b a
  • log b a = (log c a) / (log c b)
Certain rules possess distinct designations; for instance, logb (xy) = logb x + logb y is referred to as the logarithmic product formula. Similarly, the table below encompasses all the properties accompanied by their respective appellations. Logarithms Formulas

Logarithmic Formulas Derivation

Presented below is the derivation process for significant logarithmic formulas. The derivation of log formulas is conducted by applying the laws governing exponents.

Download PDF Logarithms Formula

Product Formula of Logarithms

The logarithmic product formula is expressed as follows: logb (xy) = logb x + logb y. Derivation: Let's assume logb x = m and logb y = n. According to the logarithmic definition, x = bm and y = bn. Consequently, xy = bm × bn = bm + n (based on the exponent law am × an = am + n). Converting xy = bm + n into logarithmic notation, we arrive at m + n = logb xy. By substituting the values logb x = m and logb y = n, logb (xy) = logb x + logb y.

Also Check - Rational Number Formula

Quotient Formula Of Logarithms

The logarithmic quotient formula can be expressed as follows: logb (x/y) = logb x - logb y. Derivation: Let's assume logb x = m and logb y = n. According to the logarithmic definition, x = bm and y = bn. Therefore, x/y = bm / bn = bm - n (applying the exponent law am / an = am - n). Transforming x/y = bm - n into logarithmic representation, we obtain m - n = logb (x/y). By substituting the values logb x = m and logb y = n, logb (x/y) = logb x - logb y.

Also Check - Linear Equation Formula

Power Formula of Logarithms

The logarithmic power formula states that logb ax = x logb a. Derivation: Assume logb a = m. Based on the logarithmic definition, a = bm. By raising both sides to the power of x, we arrive at ax = (bm)x ax = bmx (applying the exponent law, (am)n = amn) Reverting this back to logarithmic notation, logb ax = m x Substitute m = logb a into this equation, logb ax = x logb a.

Also Check - Quadrilaterals Formula

Change Of Base Formula Of Logarithms

The logarithmic change of base formula is expressed as follows: logb a = (logc a) / (logc b). Derivation: Let's assume that logb a = x, logc a = y, and logc b = z. Converting these into exponential forms, a = bx ... (1) a = cy ... (2) b = cz ... (3) From equation (1) and (2), bx = cy (cz)x = cy (using equation 3) czx = cy Given that the bases are the same, the exponents must also be equal. zx = y (or) x = y / z. By substituting the values of x, y, and z back into the equation, logb a = (logc a) / (logc b).

Logarithm Applications

Logarithms find diverse applications in both mathematical and real-world scenarios. Let's explore a handful of instances showcasing how logarithms are integrated into everyday life:
  • Earthquake Magnitude : Logarithms are employed to compute the magnitude of earthquakes.
  • Decibel Measurements : Logarithms are utilized to quantify noise levels in decibels, such as the resonance of a bell.
  • Chemical pH : Logarithms play a role in Chemistry by determining acidity or pH levels.
  • Financial Growth : They assist in calculating monetary growth at specified interest rates.
  • Exponential Processes : Logarithms are commonly used to determine the exponential decay or growth of phenomena, like bacterial propagation or radioactive decay.
  • Computation Transformation : Logarithms serve to convert multiplication problems into addition and vice versa.
Instead of performing straightforward calculations, we can use a logarithm table to find the logarithm of an integer. Before calculating a number's logarithm, understanding its characteristic and mantissa components is crucial. Characteristic Part: This denotes the integral segment of a number. For numbers greater than one, the characteristic is positive. If the characteristic is one less than the number of digits to the left of the decimal point in a given integer, it's negative. For numbers smaller than one, the characteristic is negative, with its magnitude being one greater than the number of zeros to the right of the decimal point. Mantissa Part: The mantissa constitutes the decimal portion of the logarithm and should always be positive. If the mantissa takes on a negative value, it is converted to a positive value.

How Do You Use A Log Table?

Here is a breakdown of the procedure for determining the logarithmic value of a number using a logarithm table. It's essential to comprehend the usage of the logarithm table, which is a valuable resource for value determination. Step 1: Grasp the Concept of Logarithms. Each logarithm table corresponds to a specific base, with log base 10 being the commonly utilized form. Step 2: Identify Characteristics and Mantissa. To find the log value of a number like 15.27, split it into its characteristic and mantissa components. Characteristic Part = 15 Mantissa Part = 27 Step 3: Utilize the Shared Log Table. Refer to row 15 and locate column 2, noting the corresponding value. In this case, it's 1818. Step 4: Calculate the Mean Difference. Slide your finger along row 15 and find the value associated with column 7, which is 20. Step 5: Combine Results from Steps 3 and 4. Add 1818 and 20 to get 1838, representing the mantissa. Step 6: Determine the Characteristic. Since the number lies between 10 and 100 (101 and 102), the characteristic should be 1. Step 7: Combine the Characteristic and Mantissa. Ultimately, the value is obtained as 1.1838.

Logarithms Formulas FAQs

What are the logarithmic formulas?

ormulas. logb 1 = 0 logb b = 1 logb (xy) = logb x + logb y logb (x / y) = logb x - logb y logb ax = x logb a logb a = (logc a) / (logc b)

What is the different use of log formulas?

Logs come to the rescue when dealing with problems that resist solutions through exponent properties. Logarithmic formulas serve the purpose of either condensing a series of logarithms into a singular logarithmic expression or expanding a single logarithm into multiple terms.

Explain the term natural Log.

The natural logarithmic formulas mirror those of regular logarithmic expressions, with the exception that "log with a specific base" is substituted by "ln". Presented below are the key natural logarithm formulas: ln (xy) = ln x + ln y ln (x / y) = ln x - ln y ln ax = x ln a

How To Derive Log Formulas?

Logarithmic formulas are derived through the utilization of exponent laws. The process of derivation also involves employing the logarithmic definition. This entails converting between logarithmic and exponential forms during the derivation.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.