
Complex Numbers take the form a + ib, where 'a' and 'b' are real numbers, and 'i' (iota) represents the imaginary component, equal to the square root of -1. Complex numbers are commonly expressed in rectangular or standard form. For instance, 10 + 5i is a complex number, where 10 signifies the real component, and 5i signifies the imaginary part. Depending on the values of 'a' and 'b,' complex numbers can be entirely real or purely imaginary. When 'a' is equal to 0 in the expression a + ib, the result is a purely imaginary number represented by ib. Conversely, when 'b' is set to 0, the outcome is 'a,' which is a purely real number.
What is Dividing Complex Numbers?
Dividing complex numbers follows the same mathematical principles as dividing real numbers. If we have two complex numbers, z1 = x1 + iy1 and z2 = x2 + iy2, the division of complex numbers z1 and z2 can be expressed mathematically as:
z1 / z2 = (x1 + iy1) / (x2 + iy2)
Steps for Dividing Complex Numbers
Now that we understand the concept of dividing complex numbers, let's delve into the step-by-step process for dividing them:
Start by finding the conjugate of the complex number in the denominator of the fraction.
Proceed to multiply both the numerator and the denominator of the complex fraction by the conjugate.
Utilize the algebraic identity (a + b)(a - b) = a 2 - b 2 in the denominator, taking into account that i 2 equals -1.
Apply the distributive property in the numerator and simplify the expression.
Finally, separate the resulting complex number into its real and imaginary parts for a clearer representation.
Dividing Two Complex Numbers
The division of two complex numbers differs from dividing real numbers and is more akin to the concept of rationalizing the denominator, often encountered when dealing with fractions containing irrational numbers in their denominators. Here are the steps involved in the division of complex numbers:
Ensure that both the numerator and denominator are in the standard form of complex numbers, represented as z = a + ib.
Compute the complex conjugate of the denominator. If the denominator is c + id, its conjugate is c − id.
Multiply both the numerator and denominator by the conjugate of the denominator.
Utilize the difference of squares formula to simplify the denominator.
Divide the resulting complex number into its real and imaginary parts.
The division process for two complex numbers, z1 = x + iy and z2 = a + ib, can be summarized as follows:
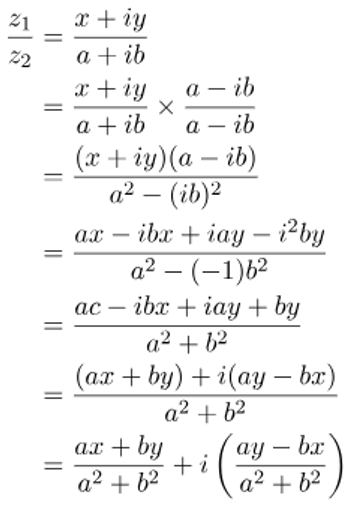
Also Check – Probability Formula
Division of Complex Numbers in Polar Form
To divide the complex number z1, represented as r1(cosθ1 + isinθ1), by the complex number z2, represented as r2(cosθ2 + isinθ2), the division is computed as follows:
z 1 / z 2 = r 1 (cosθ 1 + isinθ 1 ) / r 2 (cosθ 2 + isinθ 2 )
This can be simplified step by step as follows:
Multiply the numerator and denominator by the conjugate of the denominator, which is r2(cosθ2 - i sinθ2):
= r 1 (cosθ 1 + isinθ 1 ) * r 2 (cosθ 2 - isinθ 2 ) / [r 2 (cosθ 2 + isinθ 2 ) * r 2 (cosθ 2 - i sinθ 2 )]
In the denominator, apply the difference of squares formula (a 2 - b 2 = (a + b)(a - b)) and consider that i 2 equals -1:
= r 1 (cosθ 1 + i sinθ 1 ) * r 2 (cosθ 2 - isinθ 2 ) / [r2 2 (cos 2 θ 2 - (-1)(sin 2 θ 2 ))]
Continue simplifying:
= r1(cosθ1 + isinθ1) * r2(cosθ2 - isinθ2) / [r2^2(cos^2θ2 + sin^2θ2)]
Further simplify:
= r 1 * r 2 * [cos(θ 1 - θ 2 ) + i sin(θ 1 - θ 2 )] / [r2 2 ]
Define θ as θ 1 - θ 2 and r as the product of r 1 and r 2 :
= r * [cosθ + i sinθ]
Therefore, the division of complex numbers z 1 = r 1 (cosθ 1 + i sinθ 1) and z 2 = r 2 (cosθ 2 + i sinθ 2 ) in polar form is given by the result r(cosθ + i sinθ), where θ is θ 1 - θ 2 , and r is the product of r 1 and r 2 :
z 1 / z 2 = r(cosθ + i sinθ)
Also Check – Triangles Formula
Important Notes on Dividing Complex Numbers
To divide a complex number a + ib by c + id, you can utilize the concept of the complex conjugate to simplify the division process. Here are the steps:
Find the complex conjugate of the denominator, which is c - id.
Multiply both the numerator and denominator of the fraction a + ib / c + id by the conjugate of the denominator, which is c - id.
Apply the distributive property and simplify the expression.
This method helps eliminate the imaginary parts from the denominator, making the division more straightforward.
Additionally, the modulus or absolute value of a complex number z = a + ib is calculated as |z| = √(a 2 + b 2 ). This formula gives you the length or magnitude of the complex number in the complex plane.
Also Check – Introduction to Euclid Formula
Examples
Problem 1. Solve:
![]()
Solution:
The denominator 2i can be represented as 0 + 2i.
To find the conjugate of the denominator, we change the sign of the imaginary part, which results in 0 − 2i.
Next, we multiply both the numerator and denominator by 0 + 2i.
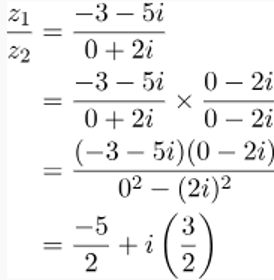
Problem 2. Solve:
![]()
Solution:
Conjugate of the denominator = 3 + 2i
Multiply both the numerator and denominator by 3 – 2i.
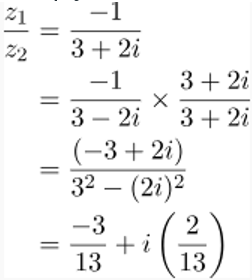
Complex Number Division Formula FAQs
Q1. What is the formula for dividing complex numbers?
Q2. Why do we multiply by the complex conjugate when dividing complex numbers?
Q3. What is the complex conjugate of a complex number?
Q4. How do you calculate the modulus or absolute value of a complex number?
Q5. Can you provide an example of dividing complex numbers using the formula?










