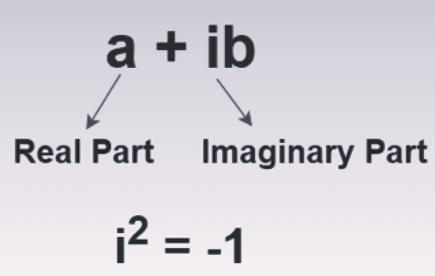
Complex Number Power Formula: Definition and Solved Examples

Complex numbers can be expressed in the form a + ib, where 'a' and 'b' are real numbers, and 'i' (also known as 'iota') represents the imaginary component, with a value equal to the square root of -1. Complex numbers are commonly represented in rectangular or standard form. For instance, the complex number 10 + 5i consists of a real component (10) and an imaginary part (5i).

The nature of complex numbers can vary based on the values of 'a' and 'b'; they can be entirely real or purely imaginary. When 'a' equals 0 in the expression a + ib, the result is purely imaginary (ib). Conversely, when 'b' equals 0, the result is a strictly real number (a).

In this article, we will delve into complex number power formulas, explore examples, and provide detailed insights into this topic.

Complex Number Definition

A complex number is defined as a number represented in the form a + ib, where 'i' is the imaginary unit with a value of √(-1), and 'a' and 'b' are real numbers. A complex number can be broken down into two components: the real part, denoted by 'a,' and the imaginary part, expressed as 'ib.'

Complex Number Power Formula

The formula to calculate the power of a complex number (a + ib) to an integer 'n' is known as the Complex Number Power Formula. It is given by:

(a + ib) ⁿ = (a ⁿ ) + nC1(a ^(n-1) )(ib) - nC2(a ^(n-2) )(ib) ² + ... + nCn-1(a)(ib) ^(n-1) + (ib) ⁿ

In this formula:

'a' and 'b' are real numbers.

'i' represents the imaginary unit (√(-1)).

'n' is a non-negative integer.

nCk represents the binomial coefficient, which is the number of ways to choose 'k' items from 'n' distinct items without regard to order.

This formula allows you to calculate the result of raising a complex number to a given integer exponent 'n'. The result will also be a complex number with both real and imaginary parts.

Keep in mind that for fractional or non-integer exponents, you may need to use more advanced methods, such as De Moivre's Theorem, to calculate the power of a complex number.

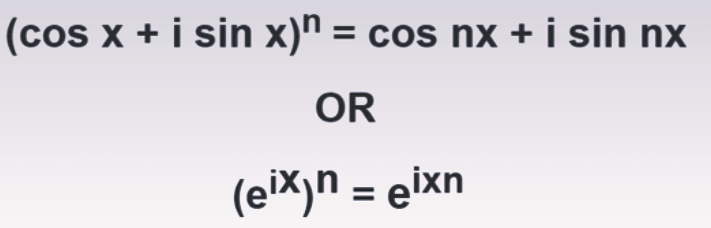
Also Check – Line and Angles Formula

Complex Number Power Formula Derivation

P(n): (cos x + i sin x) ⁿ = cos(nx) + isin(nx) ⇢ (1)

For n = 1, we have

P(1) = (cos x + i sin x) ¹

P(1) = cos(1x) + i sin(1x)

P(1) = cos(x) + i sin(x)

That is true and thus, P(1) is true.

Assuming P(k) is true, i.e.

P(k) = (cos x + i sin x) ^k = cos(kx) + i sin(kx) ⇢  (2)

Also Check – Logarithm Formula

Now, we just have to prove that the P(k+1) is also true.

P(k+1) = (cos x + i sin x) ^k+1

P(k+1) = (cos x + i sin x)k (cos x + i sin x)

P(k+1) = (cos (kx) + i sin (kx)) (cos x + i sin x) [Using (i)]

P(k+1) = cos (kx) cos x − sin(kx) sinx + i (sin(kx) cosx + cos(kx) sinx)

P(k+1) = cos {(k + 1)x} + i sin {(k + 1)x}

P(k+1) = (cos x + i sin x) ^k+1 = cos {(k + 1)x} + i sin {(k + 1)x}

Thus, P(k+1) is also true, thus by the principle of mathematical induction, P(n) is true.

Hence the result is proved.