Lines and Angles Formula
are fundamental concepts that established through the notions of lines and angles, forming the bedrock of the subject. A line is characterized as an unbroken sequence of closely positioned points extending infinitely in two opposite directions. Its sole dimension is its length, as exemplified by a horizontal stroke on a sheet of paper. Conversely, an angle emerges as a geometric figure formed by the convergence of two rays at a shared endpoint. These angles are quantified in degrees using a protractor. Every geometric shape incorporates lines and angles within its framework. In this lesson, we shall delve deeper into the diverse classifications of lines and angles.
Definition of Lines and Angles
Ancient mathematicians introduced the notion of lines to symbolize linear entities devoid of width or depth. While lines possess straightforward comprehension, angles are geometric constructs arising from the intersection of line segments, lines, or rays. An angle takes form when two rays intersect within the same plane.
Lines
A line constitutes a one-dimensional entity that extends infinitely in both directions, devoid of any width. It comprises an infinite series of closely positioned points. Euclid characterizes a line as a length without breadth. In a Cartesian plane, it is represented by the linear equation ax + by = c. Take note of the line depicted in the provided illustration.
Rays
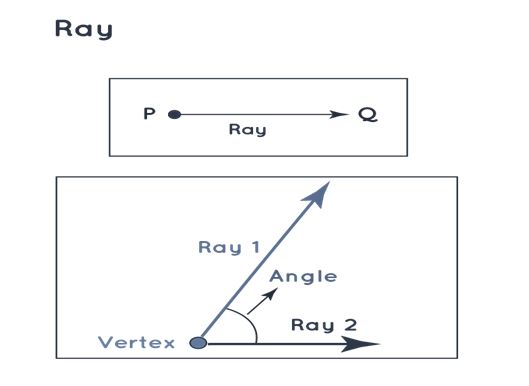
Rays are lines that initiate from a single point, acting as the starting point, and then extend infinitely in one direction without cessation. They progress in a singular direction indefinitely. When two rays are connected by aligning their endpoints, they generate an angle. Their representation is denoted as
PQ.
Line Segment
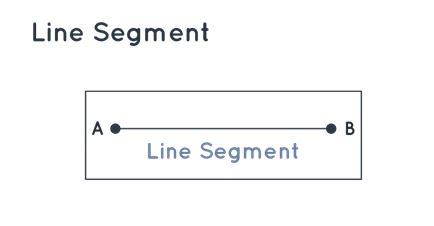
When a line possesses two distinct endpoints, it is recognized as a line segment. The measurement of a line segment's length is feasible, and it is denoted as.
Download PDF Lines And Angle Formula
Angles
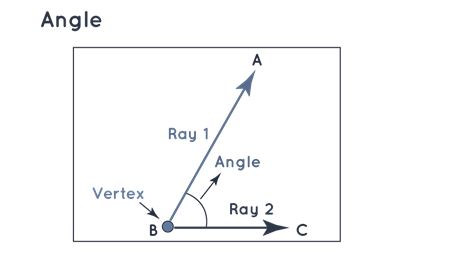
When two rays intersect at a particular point, they give rise to an angle. Typically quantified in degrees and symbolized by
∘
(the degree symbol), angles provide a measure of rotation. An angle's value can range from 0
∘
to 360
∘
, represented by the symbol
∠
. Take note of the illustration below, depicting
∠
ABC.
Types of Lines and Angles
Lines can be categorized into various types based on their distinctive characteristics. The subsequent table outlines the diverse classifications of lines.
|
Type of Lines
|
Description
|
Illustration
|
|
Horizontal Line
|
These lines are parallel to the X-axis
and
perpendicular
to the y-axis
|
|
|
Vertical Line
|
These lines are parallel to the y-axis and
perpendicular
to the x-axis
|
|
|
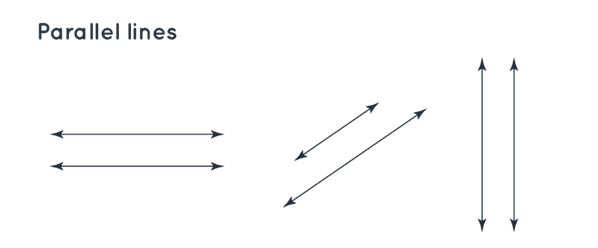
Parallel Lines
|
When two straight lines move alongside and maintain a constant distance between each other up to infinity, they are known as parallel lines. The symbol || is used to represent parallel lines.
|
|
|
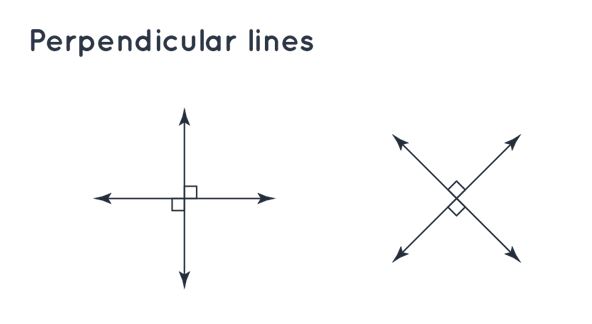
Perpendicular Lines
|
When two lines intersect each other at an angle of 90°, they are known as perpendicular lines. Perpendicular lines are denoted by the symbol of
⊥
|
|
|
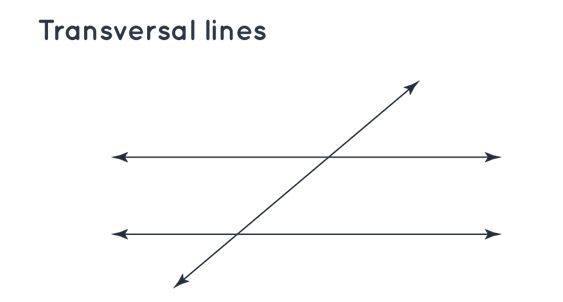
Transversal Lines
|
When a line intersects two lines at different respective points, then it is known as a transversal line.
|
|
Types of Angles
Angles can be classified into distinct categories according to their measurements. Generally, angles fall into six types:
Angle Based on Rotation
Angles can be classified into two types based on the direction of measurement or rotation:
Positive Angles:
An angle measured in the counterclockwise (anti-clockwise) direction is referred to as a positive angle. In simpler terms, positive angles are angles that are rotated from the reference point in the anti-clockwise direction.
Negative Angles:
Negative angles are angles measured in a clockwise direction from the reference point. In simpler terms, negative angles are angles that are rotated from the reference point in the clockwise direction.
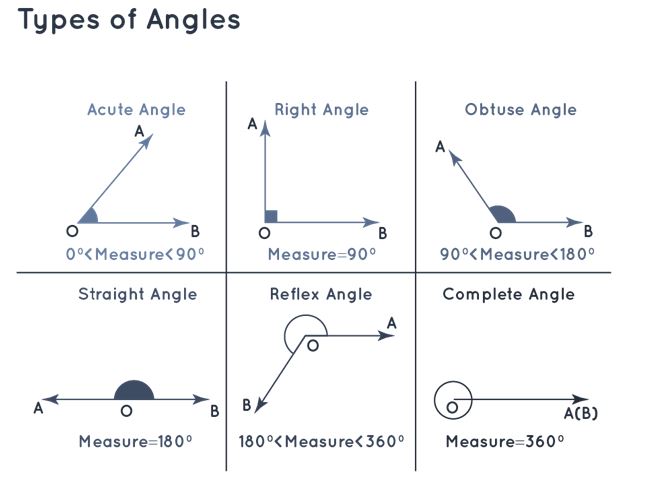
Acute angle
: An angle is considered acute if its measurement is less than 90
∘
.
Here, (
∠
ABC = 40
∘
) < 90
∘
Obtuse angle
: An angle falls under the obtuse category if its measurement is greater than 90
∘
but less than 180
∘
.
Here, 90
∘
< (
∠
ABC = 117
∘
) <180
∘
Right angle
: An angle is classified as a right angle when its measurement precisely equals 90
∘
.
Here,
∠
ABC = 90
∘
Straight angle
: An angle takes on the designation of a straight angle if its measurement is 180
∘
.
Here,
∠
AOB = 180
∘
Reflex angle
: An angle is categorized as a reflex angle if its measurement is greater than 180
∘
but less than 360
∘
.
180
∘
< (Reflex Angle = 330
∘
) < 360
∘
Complete angle
: An angle is referred to as a complete angle when its measurement amounts to 360
∘
.
Angle = 360
∘
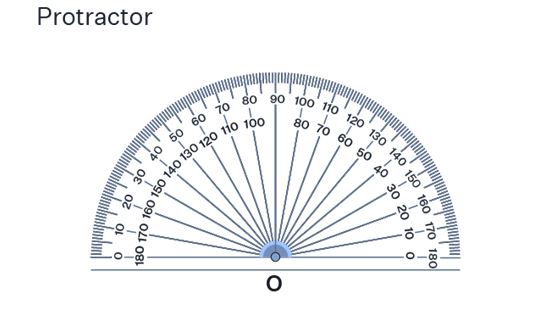
The most effective method for angle measurement involves the utilization of a protractor. A protractor is a measuring tool designed in the form of a semi-circle. This translucent instrument aids in quantifying angles by degrees. It displays degrees in a clockwise sequence from 0° to 180° on the outer scale and in an anti-clockwise sequence from 0° to 180° on the inner scale.
Also Read -
Rational Numbers Formula
Properties of Lines and Angles
Having observed the various types of lines and angles, it's evident that each possesses distinct properties. Nonetheless, there exist fundamental shared properties of both lines and angles that merit discussion.
Properties of Lines
Lines can be described as a collection of an infinite multitude of closely adjacent points.
They extend ceaselessly in both directions.
They exist within a one-dimensional framework and lack depth or thickness.
Also Check -
Algebra Formulas
Properties of Angles
An angle materializes as a geometric shape resulting from the intersection of two lines within the same plane.
The lines giving rise to an angle are termed as its arms or sides, while the point at which they converge is identified as its vertex.
Tips on Lines and Angles
Outlined below are several guidelines to bear in mind when delving into the study of lines and angles:
-
Every geometric shape incorporates both angles and lines.
-
A line constitutes a one-dimensional entity without breadth, extending infinitely in both directions.
-
Rays, characterized by one end as the starting point and the other end extending infinitely, are utilized to construct angles.
-
Angles arise from the intersection of two rays at a specific point.
Also Check -
Coordinate Geometry Formula
Important Notes
-
0°< Acute angle < 90°
-
90°< Obtuse angle < 180°
-
180° < Reflex angle < 360°
-
A right angle is equal to 90°
-
A straight angle is equal to 180°.
