Coordinate Geometry Class 9 Math Formula Each spot on our planet possesses coordinates that facilitate its precise positioning on the global map. The Earth's coordinate framework comprises imaginary lines known as latitudes and longitudes. These coordinates originate from the zero-degree Greenwich Longitude' and the zero-degree 'Equator Latitude.' Similarly, for pinpointing locations on a plane or paper, we employ coordinate axes that encompass the horizontal x-axis and the vertical y-axis.
Coordinate geometry encompasses the examination of geometric shapes through their representation on the coordinate axes. By plotting them, figures like straight lines, curves, circles, ellipses, hyperbolas, and polygons can be accurately delineated and proportionally showcased. Moreover, coordinate geometry facilitates algebraic manipulation and the analysis of geometric shape properties, all thanks to the utilization of the coordinate system.
Also Check -
Data Handling Formula
What Is Coordinate Geometry?
Coordinate geometry constitutes a significant facet of mathematics, contributing to the graphical representation of geometric shapes within a two-dimensional plane while also fostering comprehension of their inherent properties. Here, we embark on an exploration of the coordinate plane and the concept of point coordinates, aiming to establish an introductory grasp of the realm of coordinate geometry.
Also Check -
Sequence and Series Formula
Coordinate Plane
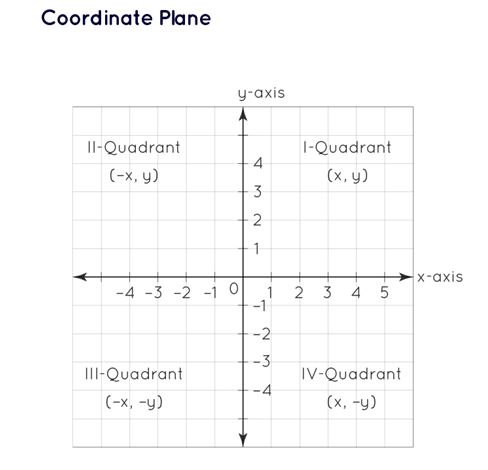
The Cartesian plane, also known as the coordinate plane, effectively divides the plane into two dimensions, providing a practical means of pinpointing locations. It consists of two axes: the horizontal x-axis and the vertical y-axis. These axes subdivide the plane into four quadrants, with the point of intersection called the origin (0, 0). In this context, any point on the coordinate plane is denoted as (x, y), where 'x' signifies the position of the point in relation to the x-axis, and 'y' indicates the position with respect to the y-axis.
Download PDF Coordinate Geometry Class 9 Formula
Distinct properties characterize points located within the four quadrants:
-
The origin, labeled O, is the juncture of the x-axis and the y-axis, with coordinates (0, 0).
-
The x-axis's right side from the origin is the positive x-axis, while the left side is the negative x-axis. Similarly, the y-axis's upper section from the origin is the positive y-axis, and the lower section is the negative y-axis.
-
Points in the first quadrant (x, y) possess both positive x and y values, plotted with reference to both positive axes.
-
Points in the second quadrant (-x, y) are situated along the negative x-axis but share a positive y-coordinate.
-
Points in the third quadrant (-x, -y) exhibit negative values on both axes.
-
Points in the fourth quadrant (x, -y) boast a positive x-coordinate but a negative y-coordinate.
Coordinates of a Point
A coordinate serves as a positional identifier for a point within a given space. In a two-dimensional context, a point's coordinates are represented as (x, y). Let's delve into two pivotal terms associated with this concept:
-
Abscissa:
This corresponds to the 'x' value in the point (x, y). It signifies the distance of the point along the x-axis, measured from the origin.
-
Ordinate:
This denotes the 'y' value in the point (x, y). It signifies the perpendicular distance of the point from the x-axis, running parallel to the y-axis.
The utilization of point coordinates enables the execution of various operations, including distance calculation, midpoint determination, slope calculation of a line, and the derivation of a line's equation.
Coordinate Geometry Formulas
Coordinate geometry formulas play a pivotal role in demonstrating the properties of lines and shapes represented on coordinate axes. These formulas encompass the distance formula, slope formula, midpoint formula, section formula, and line equation. Each formula serves a distinct purpose in coordinate geometry:
Coordinate Geometry Distance Formula
Distance Formula:
This formula computes the distance between two points (x1, y1) and (x2, y2) as the square root of the sum of squared differences in their x and y coordinates.
Distance (D) = √(x
2
−x
1
)2+(y
2
−y
1
)
2
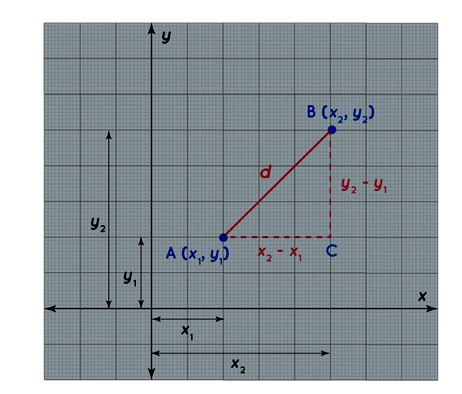
from the above figure:
By the Pythagoras’ theorem,
AB
2
= AC
2
+ BC
2
d
2
= (x
2
– x
1
)
2
+ (y
2
– y
1
)
2
Taking the square root on both sides,
d = √[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
]
This is called the distance between two points formula.
Coordinate Geometry Slope Formula
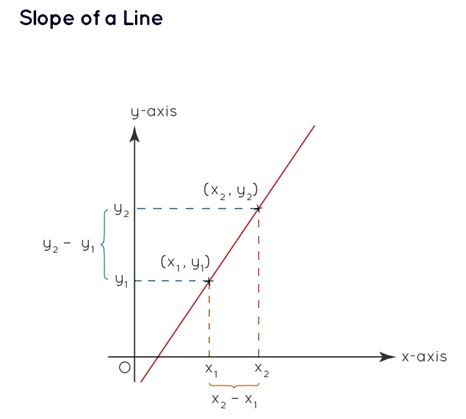
Slope Formula
:
The slope of a line can be calculated using the angle it forms with the positive x-axis or by selecting two points on the line.
Slope (m) = Tanθ = (y
2
- y
1
) / (x
2
- x
1
)
Finding Slope From a Graph
The slope of a line has only one value. So, the slopes found by Methods 1 and 2 will be equal. In addition to that, let's say we are given the equation of a straight line. The general equation can be given as,
y = mx + b
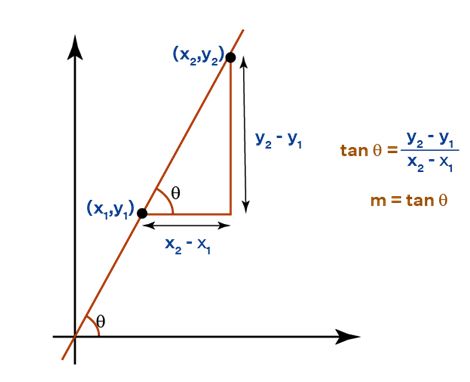
The value of the slope is given as
m;
hence the value of
m
gives the slope of any straight line.
The below-given steps can be followed to find the slope of a line such that the coordinates of two points lying on the line are: (2, 4), (1, 2)
-
Step 1: Note the coordinates of the two points lying on the line, (x
2
, y
2
), (x
1
, y
1
). Here the coordinates are given as (2, 4), (1, 2).
-
Step 2: Apply the slope of line formula, m = (y
2
- y
1
)/(x
2
- x
1
) = (4 - 2)/(2 - 1) = 2.
-
Step 3: Therefore, the slope of the given line = 2.
Coordinate Geometry Midpoint Formula
Midpoint Formula:
This formula determines the midpoint of a line joining two points (x1, y1) and (x2, y2). The midpoint's coordinates are the averages of the x and y coordinates of the given points.
Given two points A (x
1
, y
1
) and B (x
2
, y
2
), the midpoint between A and B is given by,
M(x
3
, y
3
) = ((x
1
+ x
2
)/2, (y
1
+ y
2
)/2)
where, M is the midpoint between A and B, and (x
3
, y
3
) are its coordinates.
Midpoint (x, y) = ((x1 + x2) / 2, (y1 + y2) / 2)
Coordinate Geometry Section Formula
Section Formula:
The section formula identifies the coordinates of a point that divides the line segment between two points (x1, y1) and (x2, y2) in a given ratio m:n.
Point (x, y) = ((mx2 + nx1) / (m + n), (my2 + ny1) / (m + n))
Coordinate Geometry Centroid Formula
Centroid Formula:
The centroid of a triangle formed by vertices A (x1, y1), B (x2, y2), and C (x3, y3) can be found using the formula:
Centroid (x, y) = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3)
Coordinate Geometry Area of a Triangle Formula
Area of a Triangle Formula: The area of a triangle with vertices A (x1, y1), B (x2, y2), and C (x3, y3) is computed using the formula:
Area = 0.5 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|
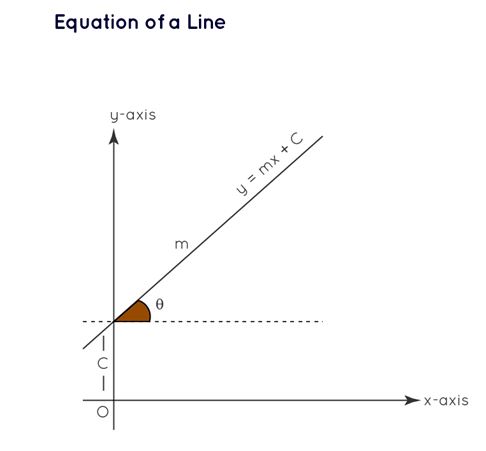
Determining the Equation of a Line in Coordinate Geometry
The equation of a line represents all points on the line through a linear equation. The standard form is ax + by + c = 0, where a, b, and c are constants. Several methods, including the slope-intercept form (y = mx + c), are used to find the equation. Other forms, such as the point-slope form, two-point form, intercept form, and normal form, provide additional perspectives on line equations.
Coordinate geometry offers a powerful toolset for understanding and analyzing geometric shapes within a coordinate system. By utilizing these concepts and formulas, mathematicians and researchers can explore the intricate relationships between points, lines, and figures on a two-dimensional plane.
Also Check -
Ratio and Proportion Formula
Points to Remember About Cartesian Coordinates
-
The slope of the x-axis holds a value of 0, while the slope of the y-axis is considered infinite (∞).
-
The x-axis is represented by the equation y = 0, and the y-axis is described by the equation x = 0.
-
A point situated on the x-axis takes the form (a, 0), whereas a point located on the y-axis is represented as (0, b).
-
The equation of a line in slope-intercept form is y = mx + c.
-
In the coordinate plane, two lines that are parallel possess equal slopes.
-
Furthermore, in the coordinate plane, when considering two perpendicular lines, the product of their slopes is equivalent to -1.
