Cos Inverse Formula: Examples, Graph, Properties, Notes

Cos Inverse , denoted as cos ^-1 (x) or acos(x), is a significant inverse trigonometric function. It serves as the inverse of the trigonometric function cosine, cos(x). It's important to emphasize that inverse cosine is not the reciprocal of cos(x). There are six inverse trigonometric functions in total: sin ^-1 x, cos ^-1 x, tan ^-1 x, csc ^-1 x, sec ^-1 x, cot ^-1 x.

The primary purpose of inverse cosine is to determine the measure of an angle using the value of the trigonometric ratio cos(x). In this article, we will explore the formulas of the inverse cosine function, its domain and range, and delve into its graph. We will also examine the derivative and integral of cos ^-1 (x)) to gain a deeper understanding of its properties.

What is Inverse Cosine?

Inverse cosine, also known as cos ^-1 (x) or arccos(x), serves as the inverse function of the cosine function and is a crucial inverse trigonometric function. If y = cos x, then x = cos ^-1 (y). Let's explore some examples to understand how the inverse cosine function works.

cos 0 = 1 ⇒ 0 = cos ^-1 (1)

cos π/3 = 1/2 ⇒ π/3 = cos ^-1 (1/2)

cos π/2 = 0 ⇒ π/2 = cos ^-1 (0)

cos π = -1 ⇒ π = cos ^-1 (-1)

In a right-angled triangle, the cosine of an angle (θ) is defined as the ratio of its adjacent side to the hypotenuse, i.e., cos(θ) = (adjacent side) / (hypotenuse). Using the definition of inverse cosine, we can express it as θ = cos ^-1 [(adjacent side) / (hypotenuse)].

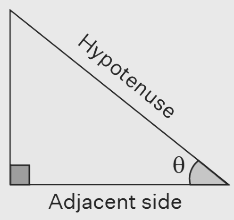
θ = cos = Adjacent side/Hypotenuse

⇒ θ = cos ^-1 (Adjacent side/Hypotenuse)

Domain and Range of Inverse Cosine

The cosine function has a domain of all real numbers (R) and a range of values between -1 and 1, [-1, 1]. For a function to have an inverse, it must be bijective, meaning it is both one-to-one (injective) and onto (surjective).

Since the cosine function is not one-to-one (it doesn't pass the horizontal line test), it doesn't have a global inverse that covers its entire domain. To find an inverse, we need to restrict the domain of the cosine function. Common choices for this restricted domain include [0, π], [π, 2π], [-π, 0], and so on, each of which corresponds to a specific branch of the inverse cosine.

The most commonly used branch is the one where the domain of the cosine function is restricted to [0, π], while the range remains [-1, 1]. This branch is known as the principal branch of the inverse cosine. Consequently, the domain of the inverse cosine function is [-1, 1], and its range is [0, π]. In other words, cos ^-1 (x) is a function from the interval [-1, 1] to [0, π].

Also Check – Quadrilaterals Formula

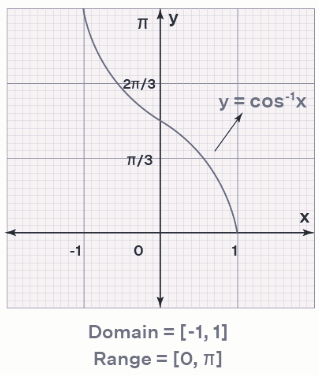
Graph of Inverse Cosine

Given that the domain and range of the inverse cosine function are [-1, 1] and [0, π], respectively, let's proceed to plot the graph of cos ^-1 (x) within the principal branch. We will use specific values of the cosine function to determine the points on the graph.

For y = cos ^-1 (x), we have the following points:

When x = 0, y = π/2

When x = 1/2, y = π/3

When x = 1, y = 0

When x = -1, y = π

When x = -1/2, y = 2π/3

Plotting these points on the graph, we can visualize the behavior of the inverse cosine function within its principal branch.

Also Check – Factorization Formula

Cos Inverse x Derivative

To find the derivative of the inverse cosine function, we start with the assumption y = cos ^-1 (x), which implies cos(y) = x. We'll differentiate both sides of this equation with respect to x using the chain rule.

Starting with cos(y) = x:

Differentiate both sides with respect to x:

d(cos(y))/dx = dx/dx

Apply the derivative of cosine, which is -sin(y), and the derivative of x with respect to x, which is 1:

-sin(y) dy/dx = 1

Solve for dy/dx:

dy/dx = -1/sin(y) ---- (1)

Now, we can find sin(y) in terms of x using the identity cos ² y + sin ² y = 1, where cos(y) = x:

sin ² y + x ² = 1

sin ² y = 1 - x ²

sin y = √(1 - x ² )

Substituting sin(y) = √(1 - x ² ) into equation (1), we get the derivative of the inverse cosine function:

dy/dx = -1/√(1 - x ² )

It's important to note that the derivative is not defined at x = -1 and x = 1 because these values make the denominator √(1 - x ² ) equal to 0. Therefore, the derivative of cos ^-1 (x) is -1/√(1 - x ² ), where -1 < x < 1.

Inverse Cosine Integration

To find the integral of inverse cosine, ∫cos ^-1 x dx, we will use the integration by parts method (ILATE).

∫cos ^-1 x = ∫cos ^-1 x · 1 dx

Using the integration by parts formula:

∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C

Here f(x) = cos ^-1 x and g(x) = 1.

∫cos ^-1 x · 1 dx = cos ^-1 x ∫1 dx - ∫ [d(cos ^-1 x)/dx ∫1 dx]dx + C

∫cos ^-1 x dx = cos ^-1 x . (x) - ∫ [-1/√(1 - x²)] x dx + C

Now, let's evaluate the integral ∫ [-1/√(1 - x ² )] x dx using the substitution method. Assume 1-x ² = u. Then -2x dx = du (or) x dx = -1/2 du.

∫cos ^-1 x dx = x cos ^-1 x - ∫(-1/√u) (-1/2) du + C

= x cos ^-1 x - 1/2 ∫u ^-1/2 du + C

= x cos ^-1 x - (1/2) (u ^1/2 /(1/2)) + C

= x cos ^-1 x - √u + C

= x cos ^-1 x - √(1 - x²) + C

Therefore, ∫cos ^-1 x dx = x cos ^-1 x - √(1 - x²) + C

Also Check – Comparing Quantities Formula

Properties of Inverse Cosine

Here are some important properties and formulas related to the inverse cosine function (cos ^-1 x):

cos(cos ^-1 x) = x only when x ∈ [-1, 1] (Note: When x ∉ [-1, 1], cos(cos ^-1 x) is undefined.)

cos ^-1 (cos x) = x, only when x ∈ [0, π] (When x ∉ [0, π], apply the trigonometric identities to find the equivalent angle of x that lies in [0, π])

cos ^-1 (-x) = π - cos ^-1 x

cos ^-1 (1/x) = sec ^-1 x, when |x| ≥ 1

sin ^-1 x + cos ^-1 x = π/2, when x ∈ [-1, 1]

The derivative of cos ^-1 x with respect to x is -1/√(1 - x ² ), valid for -1 < x < 1.

The integral of cos ^-1 x dx = x cos ^-1 x - √(1 - x²) + C, where C is the constant of integration.

These properties and formulas are helpful in solving problems involving the inverse cosine function in trigonometry.

Important Notes on Cos Inverse x

Inverse cosine is NOT the same as (cos x) ^-1 as (cos x) ^-1 = 1/(cos x) = sec x.

θ = cos ^-1 [ (adjacent side) / (hypotenuse) ], θ ∈ [0, π]

d(cos ^-1 x)/dx = -1/√(1 - x ² ), -1 < x < 1

∫cos ^-1 x dx = x cos ^-1 x - √(1 - x²) + C

cos ^-1 (-x) = π - cos ^-1 x