A
Quadrilaterals Formula
is a four-sided closed figure and it is also a type of polygon that has four edges, four angles, and four corners or vertices. Basically, the word quadrilateral is derived from the Latin words “quad”, which means a variant of four, and “latus”, which means side. Sometimes it is also known as tetragon, taken from the Greek word “tetra”, which also means four, and “gon” means corner or angle.
A quadrilateral is made by simply joining the four non-collinear points and the very important thing to remember about the quadrilateral is that the sum of its interior angles is always equal to 360 degrees.
It is not compulsory that all four sides of a quadrilateral should be of equal in length. Hence, there exist different forms of quadrilaterals depending on their sides and angles.
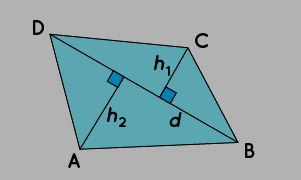
From the above figure, we have two triangles namely BCD and ABD
On finding the areas of the given triangles separately, we get that
The area of the triangle BCD = (1/2) × d × h1
The area of the triangle ABD = (1/2) × d × h2
The area of the quadrilateral ABCD = Sum of areas of ΔBCD and ΔABD.
Thus, the area of the quadrilateral ABCD = (1/2) × d × h1 + (1/2) × d × h2 = (1/2) × d × (h1 + h2).
Hence, the area of the quadrilateral formula, when one of the diagonals and the heights of the triangles (formed by the given diagonal) are given, is,
Area = (1/2) × Diagonal × (Sum of heights)
Properties Of Quadrilateral
-
Each quadrilateral consists of 4 points and 4 sides surrounding 4 angles.
-
The sum of its interior angles is 360 degrees.
-
A quadrilateral usually has sides of different lengths and angles of different lengths. However, squares, rectangles, parallelograms, etc. are special types of quadrilaterals with equal sides and angles.
Also Read - Linear Equation Formula
Area Of Quadrilateral Using Heron’s Formula
The formula of Heron is used to calculate the area of a triangle given the three sides of the triangle. Follow the given procedure to find the area of a quadrilateral.
Step 1: Divide the quadrilateral into two triangles using a diagonal whose diagonal length is known.
Step 2: Now apply Heron's formula to each triangle to find the area of the quadrilateral. [If a, b, c are the sides of a triangle, Heron's formula for finding the area of a triangle is Area of triangle = √[s(s-a)(s-b)(s-c)] square units Where "s" is the semicircle of the triangle equal to (a b c)/2. ]
Step 3: Now add the area of the two triangles to get the area of the quadrilateral
.
Area of Quadrilateral Using Sides
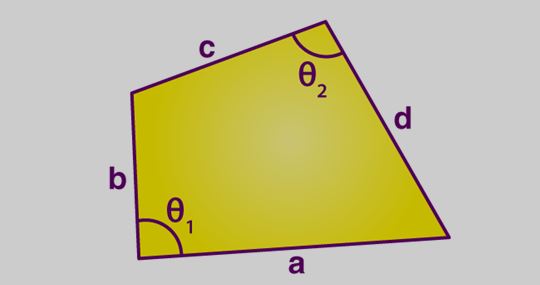
if the sides of a quadrilateral (a, b, c, d) is already given, and two of its opposite angles (θ
1
and θ
2
) are given, then the area of the quadrilateral can be calculated as follows:
Where “s” is the semi-perimeter of the quadrilateral.
(i.e.) s = (a+b+c+d)/2
And, θ= θ
1
+θ
2
Also Read - Absolute Value Formula
Area of Quadrilateral with Vertices
In coordinate geometry, the area of the quadrilateral can be calculated using the vertices quadrilateral.
Let A(x
1
, y
1
), B(x
2
, y
2
), C(x
3
, y
3
) and D(x
4
, y
4
) be the vertices of a quadrilateral ABCD.
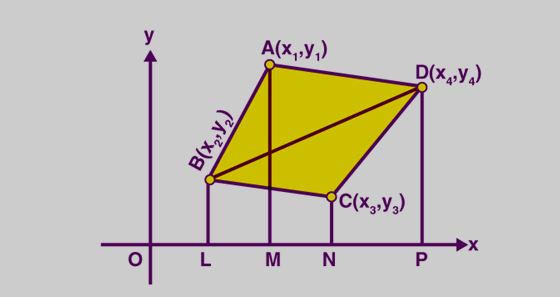
FORMULA 1:
To calculate the area of the quadrilateral ABCD using the given vertices, So, we first choose the vertices A(x
1
, y
1
), B(x
2
, y
2
), C(x
3
, y
3
) and D(x
4
, y
4
) of the quadrilateral ABCD in an order (counterclockwise direction) and write them column-wise format as it is shown below.'
Study the directions given in the dark arrows, and add the diagonal products, i.e., x
1
y
2
, x
2
y
3
, x
3
y
4
, and x
4
y
1
.
(x
1
y
2
+ x
2
y
3
+ x
3
y
4
+ x
4
y
1
)….(i)
Now, consider the dotted arrows and add the diagonal products, i.e., x
2
y
1
, x
3
y
2
, x
4
y
3
, and x
1
y
4
.
(x
2
y
1
+ x
3
y
2
+ x
4
y
3
+ x
1
y
4
)….(ii)
Subtract (ii) from (i) and multiply the difference by 1/2.
(1/2) ⋅ [(x
1
y
2
+ x
2
y
3
+ x
3
y
4
+ x
4
y
1
) – (x
2
y
1
+ x
3
y
2
+ x
4
y
3
+ x
1
y
4
)]
Therefore, the formula for the area of the quadrilateral using vertices is:
A =(1/2) ⋅ [(x
1
y
2
+ x
2
y
3
+ x
3
y
4
+ x
4
y
1
) – (x
2
y
1
+ x
3
y
2
+ x
4
y
3
+ x
1
y
4
)]
