Cosec Cot Formula with Solved Examples

Trigonometry is the mathematical study that explores the connections between angles, heights, and lengths within triangles. This branch of mathematics finds numerous practical applications in various fields such as engineering, architectural design, astronomy, and physics.

The trigonometric identities, a crucial part of trigonometry, are highly valuable and widely applicable across many domains.

Trigonometry encompasses six primary functions: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). Each of these functions has its unique formulas, and they rely on the relationships between the angles and sides of right-angled triangles.

The fundamental concept in trigonometry revolves around trigonometric ratios, which involve the measures of angles and the lengths of sides. These ratios provide essential tools for solving problems related to angles and side lengths.

In the context of right-angled triangles, trigonometry makes use of the hypotenuse, base, and perpendicular sides. These three sides enable us to calculate the values of all six trigonometric functions accurately.

What Is Cosec Cot Formula?

The cosecant (csc) and cotangent (cot) functions are two of the six trigonometric functions that are used in trigonometry. They are defined as follows:

Cosecant (csc θ): The cosecant of an angle θ in a right-angled triangle is the reciprocal of the sine of that angle. It can also be defined as the ratio of the length of the hypotenuse to the length of the side opposite to the angle θ.

csc θ = 1/sin θ

Cotangent (cot θ): The cotangent of an angle θ in a right-angled triangle is the reciprocal of the tangent of that angle. It can also be defined as the ratio of the length of the adjacent side to the length of the side opposite to the angle θ.

cot θ = 1/tan θ = cos θ/sin θ

These trigonometric functions have various properties and identities that are useful in solving trigonometric equations and problems. For example, the cosecant and cotangent functions can be expressed in terms of sine and cosine using the reciprocal identities:

csc θ = 1/sin θ

cot θ = cos θ/sin θ

These identities relate cosecant and cotangent to sine and cosine, making them convenient for calculations involving right-angled triangles and other trigonometric applications.

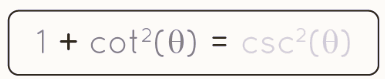
Also Check – Linear Inequalities Formula

Examples Using Cosec Cot Formula

Example 1: Prove that the given equation is true (cosec θ – cot θ) ² = (1 – cos θ)/(1 + cos θ)

Solution :

LHS = (cosec θ – cot θ) ²

= (1/sin θ−cosθ/sin θ) ²

= ((1−cos θ)/sin θ) ²

RHS = (1 – cos θ)/(1 + cos θ)

By rationalizing the denominator,

= (1−cos θ)/(1+cos θ)×(1−cos θ)(1−cos θ)

= (1−cos θ) ² /(1−cos ² θ)

= (1−cos θ) ² /sin ² θ

= ((1−cos θ)/sin θ) ²

Therefore, LHS = RHS

Also Check – Probability Formula

Example 2: Find the value for Cot P if  the value of Tan P = 4 / 3

Solution:

As per the Cotangent formula we have,

Cot P = 1 / Tan P

= 1 / (4 / 3)

= 3/4

hence, Cot P = ¾