Daily Compound Interest Formula with Solved Examples

In compound interest calculations, interest for each period is computed based on the amount from the previous period. This involves using the amount from the prior time period as the principal for the current time period. The term "compounding" refers to the practice of adding interest to the existing principal amount.

What is Daily Compound Interest Formula?

The formula for daily compound interest involves calculating interest 365 times in a year, making the value of "n" equal to 365. The daily compound interest formula is represented as:

A = P (1 + r / n) ^nt

In this formula:

P represents the principal amount.

r is the rate of interest.

t denotes the time in years.

n signifies the number of times the amount is compounded.

When compounding occurs daily, it implies that the amount compounds 365 times in a year, so n = 365.

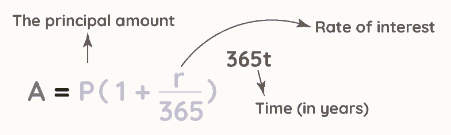
Where

A is the total amount (A = Principal + Interest)

Solved Examples Using Daily Compound Interest Formula

Example 1: You've invested $1000 in a bank where your money compounds daily at a 5% interest rate. What will be the total amount after 10 years? Calculate this using the daily compound interest formula.

Solution:

To find: The amount after 10 years.

Principal amount, P = $1000.

Interest rate, r = 5% = 0.05.

Time in years, t = 10.

Using the daily compound interest formula:

A = P (1 + r / 365) ^{365 t}

A = 1000 * (1 + 0.05/365) ^{365 × 10}

A = $1648.66

Answer: The amount after 10 years is $1648.66.

Also Check – Rational Numbers

Example 2: How long does it take for $15000 to double if it compounds daily at a 10% annual interest rate? Calculate this using the daily compound interest formula and round your answer to the nearest integer.

Solution:

To find: The time it takes for $15000 to double.

Principal amount, P = $15000.

Interest rate, r = 10% = 0.1.

Final amount, A = $30000.

Let's assume the required time in years is "t."

Using the daily compound interest formula:

A = P (1 + r / 365) ^{365 t}

30000 = 15000 * (1 + 0.1 / 365) ^{365 × 10}

Dividing both sides by 15000:

2 = (1.0002739) ^{365 t}

Taking the natural logarithm on both sides:

ln 2 = 365 × t × ln 1.0002739

t = ln 2 / (365 * ln 1.0002739)

t = 7

Answer: It takes approximately 7 years for $15000 to double.

Also Check – Cube Roots Formula

Question 1:

A sum of Rs 5000 is borrowed, and the rate is 5%. What is the daily compound interest for two years?

Solution:

Daily Compound Interest = Rs 521.80

Question 3:

A person has invested Rs 2000 in a bank where the amount gets compounded daily at an interest rate of 3%. Then what is the amount you get after 5 years? Calculate it by the daily compound interest formula?

Solution:

Amount after 5 years = Rs 2314.36

Question 4:

A sum of Rs 10000 is borrowed, and the rate is 2%. What is the daily compound interest for four years?

Solution:

Daily Compound Interest = Rs 820.80

Question 5:

A person has invested Rs 25650 in a bank where the amount gets compounded daily at an interest rate of 6%. Then what is the amount you get after 6 years? Calculate it by the daily compound interest formula? What will the daily compound interest?

Solution:

Amount after 6 years = Rs 36,732

Daily Compound Interest = Rs 11,080

Question 6:

A sum of Rs 5500 is borrowed, and the rate is 2.5%. What is the daily compound interest for 3 years?

Solution:

Daily Compound Interest = Rs 427.73

Question 7:

A sum of Rs 900 is borrowed, and the rate is 5%. What is the daily compound interest for five years?

Solution:

Daily Compound Interest = Rs 253.52

These solutions are calculated using the daily compound interest formula with the given principal, rate of interest, time, and compounding frequency (365 times per year for daily compounding).