Cube Roots Formula:
The concept of a cube involves raising a number to its own power three times, resulting in a voluminous mathematical construct. In contrast, the cube root represents the inverse operation, a process of uncovering the original number from its cubic expression. Essentially, the cube root of a value yields a number that, upon being cubed, reproduces the original value itself, creating what is known as a perfect cube. The realm of mathematics offers various methodologies for both calculating cubes and determining cube roots.
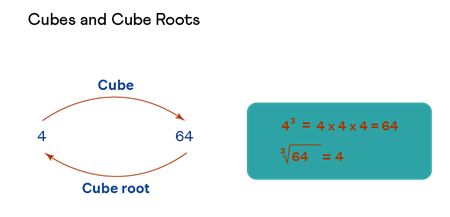
To cube a number, just use it in multiplication 3 times ...
Cube and Cube Root
Within the realm of three-dimensional geometry, the cube emerges as a distinct geometrical entity characterized by three intrinsic dimensions: Length, Breadth, and Height. Remarkably, all three dimensions in the case of a cube are congruent, rendering them equivalent in length. These equivalent dimensions are often designated as "Sides" (a) or more technically as the edges of the cube. Intriguingly, when viewed from a two-dimensional perspective, the cube presents itself as a square-like configuration.
Furthermore, the cubical form finds its embodiment in various everyday objects and structures. Common items such as ice cubes, dice, cuboidal containers, and even specific architectural spaces are intentionally crafted to adhere to the symmetrical perfection of the cubical pattern.
The Symbol for Cube Root
The representation denoting the cube root takes the form of '3√', while the symbol '(given number)3' signifies the process of calculating the cube of a provided numerical value.
Illustration:
For instance, when considering the cube root of 27 as '3√27', the result is 3. This indicates that if the number 3 is repeatedly multiplied by itself three times, or cubed, it results in 27.
Similarly, when we encounter '(5)3', the intention is to cube or multiply the value 5 by itself thrice: 5×5×5, resulting in 125.
Also Check -
Quadrilaterals Formula
Cube Root Formula
The process of determining the cube root for a provided numerical value, whether composed of identical or distinct digits, involves employing the Prime Factorization method. This technique entails factoring the given number into its smallest prime factors. Subsequently, the identical prime factors are grouped together and then cubed. The final step entails multiplying these grouped numbers to attain the cube root.
Perfect Cubes Formula
A perfect cube is an integer that can be represented as the outcome of three equal integers being multiplied together.
Take, for instance, the number 125, which qualifies as a perfect cube due to the equation 53 = 5 × 5 × 5 = 125. Conversely, 121 does not meet the criteria for being a perfect cube because there is no integer that, when multiplied three times, yields the product 121.
Also Check -
Algebra Formulas
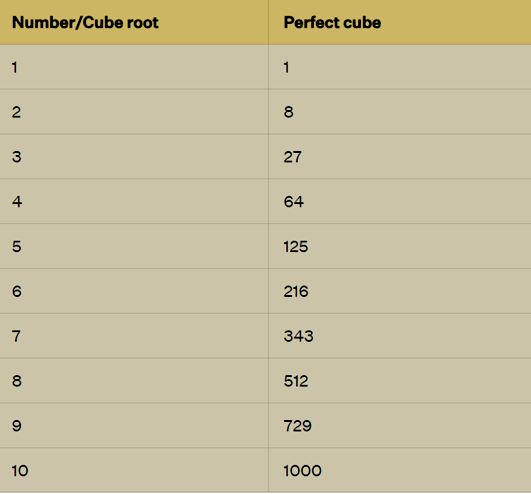
In essence, a perfect cube is a number for which its cube root is a whole number. This type of number is also referred to as a 'cube number'. Below, you will find a table enumerating the perfect cubes corresponding to the initial 10 natural numbers.
How to Find the Cube Root of a Number?
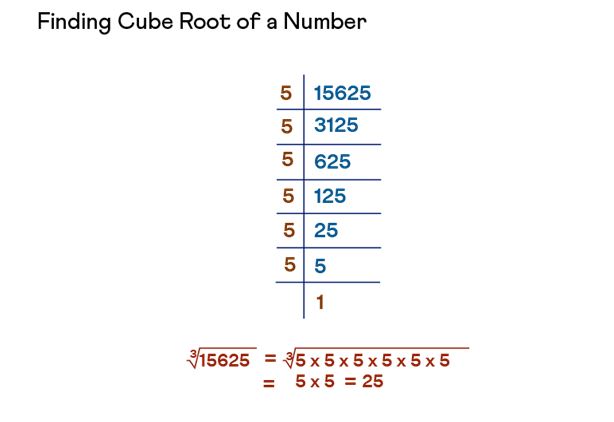
The method of prime factorization can be employed to ascertain the cube root of a given numerical value. The procedure involves the following steps:
-
Initiate the process by establishing the prime factorization of the provided number.
-
Subsequently, organize the obtained factors into sets, each consisting of three identical factors.
-
Proceed to eliminate the cube root symbol and perform a multiplication of the grouped factors. This yields the solution. If there are remaining factors that cannot be evenly grouped into sets of three, it signifies that the given number does not qualify as a perfect cube. Consequently, the cube root of that particular number cannot be determined.
Example:
Let us see how to find the cube root of 15625.
Cube Root Formula
The utilization of the cube root formula aids in the determination of the cube root for any specified numerical value, represented within a radical structure employing the symbol
∛
. The process entails the initial identification of the prime factorization of the given number, followed by the subsequent application of the cube root formula. Assume that there exists a number x, where x = y × y × y.
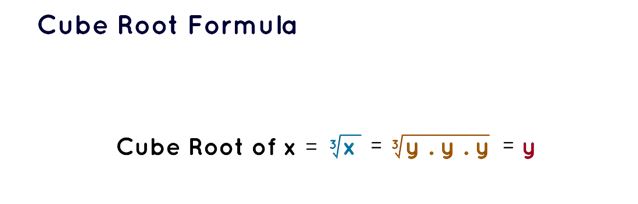
The expression for computing the cube root is as follows:
Cube root of x =
∛
x =
∛
(y × y × y) = y
In this context, y represents the cube root of the number x. This proposition also indicates that the numerical value x would qualify as a perfect cube if the variable y assumes an integer value.
Also Check -
Absolute Value Formula
Applications of Cube Root Formula
Given below are a few major applications of the cube root formula:
-
Solving any cubic equation.
-
Finding the dimensions of a cube if the volume is given.
What is the Cube of a Number?
The product obtained by tripling a number with itself three times is referred to as the cube of the original number. This nomenclature stems from its association with the volume calculation of a cube. Essentially, when a number is raised to the power of 3, it is known as the cube of that particular number. For instance, consider the cube of 3, which yields 27. This implies that 3 × 3 × 3 equals 27, succinctly expressed as 33. Similarly, the cube of 4 results in 64, and the cube of 5 evaluates to 125, and so on.
The process to find the cube of a given number involves initially multiplying the number by itself and then taking the product and multiplying it by the original number once more. To illustrate this process, let's compute the cube of 7 using the same methodology. Knowing that the cube of a number "N" is equal to N × N × N, we can determine the cube of 7 by performing the multiplication 7 × 7 × 7. To proceed, we first ascertain the product of 7 × 7, yielding 49. Subsequently, we multiply 49 by 7, resulting in 343. As such, it can be definitively stated that the cube of the number 7 is 343.
Cube of a Fraction
Just as the cube of an integer can be obtained by tripling it, the cube of a fractional value can be determined by multiplying it threefold. Consider the fraction (2/5) as an illustration: its cube can be expressed as 2/5 × 2/5 × 2/5. Upon further simplification, the cube value can be derived as (2 × 2 × 2) / (5 × 5 × 5), resulting in the fraction (23/53) which equates to 8/125
.\
Download PDF Cube Root Formula
Cube of Negative Numbers
The process to determine the cube of a negative number follows the same procedure as that of whole numbers and fractions. It's important to keep in mind that while the cube of a negative number yields a negative result, the cube of a positive number yields a positive result. Let's explore this with an example of finding the cube of -7.
We are aware that the cube of -7 can be expressed as (-7) × (-7) × (-7). To compute the cube of (-7), we initially evaluate the value of (-7) × (-7), resulting in 49. Subsequently, we calculate 49 × (-7), which equals -343. Thus, it can be concluded that the cube of the number -7 is -343.
The formula for computing the cube root of negative numbers involves the following steps:
-
Initiate the prime factorization method for the provided negative number.
-
Organize the obtained factors into groups, ensuring each group contains an identical set of factors.
-
Proceed to multiply the factors within any single group to ascertain the cube root.
-
It's noteworthy that the multiplication of three negative values results in a negative outcome, as indicated by the negative sign accompanying the cube root of a negative number.
