
Doppler Effect Formula: The Doppler Effect stands as a significant phenomenon in the field of waves, finding applications across various scientific domains. From natural physical processes to planetary movements, this effect shows whenever objects are in motion relative to the waves. In our real world surroundings, it becomes apparent, for example, when a person perceives a change in the frequency of an ambulance siren as it approaches and passes by. Given the multitude of scenarios where this effect comes into play, a thorough study of the Doppler Effect becomes imperative.
Doppler Effect Formula
The Doppler Effect, as evident in everyday experiences like the changing frequency of a train whistle, occurs when there is a relative motion between an observer and a source of waves. When an observer approaches a stationary sound source, the perceived pitch is higher than the actual pitch. Conversely, as the observer moves away from the source, the observed frequency appears lower than the actual frequency of the sound. This alteration in perceived frequency due to motion is known as the Doppler Effect.
This phenomenon extends beyond sound waves; it applies to all types of waves. Analyzing the Doppler Effect involves considering three possible cases:
- The observer is stationary while the source is in motion.
- The observer is in motion while the source remains stationary.
- Both the source and the observer are in motion.
Note: While most waves necessitate a medium for propagation, electromagnetic waves defy this requirement and can travel through a vacuum. In such instances, the scenarios where the observer is in motion while the source is stationary, and vice versa, are equivalent.
Moving Source: Stationary Observer
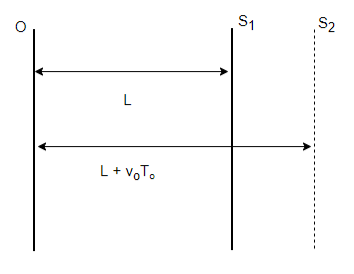
An example of a sound source approaching its observer is a train approaching a station. The illustration below depicts a scenario where the source is in motion while the observer remains stationary. The velocity of the source is represented by vs. If the actual frequency of the source is denoted as f and the observed frequency is denoted as f', with "v" representing the velocity of the sound wave, the observed frequency in this case is given by:
Doppler Effect Formula
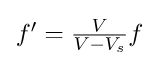
Stationary Source: Moving Observer
Consider an observer seated in a car approaching a stadium hosting a concert. This scenario illustrates a situation in which the observer is in motion and approaching the stationary source. In cases where the source is stationary and the observer is moving, the velocity of the observer is denoted by vo. If the actual frequency of the source is represented by f and the observed frequency is denoted as f', with "v" denoting the velocity of the sound wave, the observed frequency in this case is given by:
Doppler Effect Formula
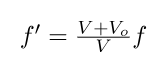
Both Source and Observer in Motion
The illustration below depicts a scenario in which both the source and the observer are in motion. The velocity of the observer is denoted by vo, while the velocity of the source is given by vs. If the actual frequency of the source is represented by f and the observed frequency is denoted as f', with "v" representing the velocity of the sound wave, the observed frequency in this case is given by:
Doppler Effect Formula
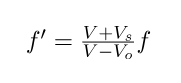
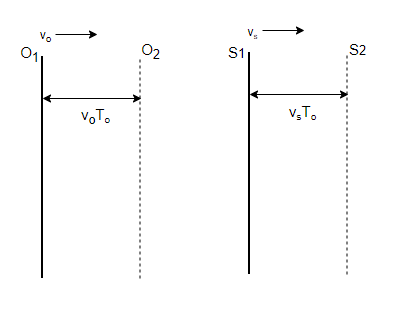
Note that the third case holds both of the preceding two cases, making it a generalization of both. In the event of a reversal in the direction of velocity, the signs of the velocities are adjusted accordingly.
Limitations of the Doppler Effect
Despite its widespread applications in various fields involving waves, the Doppler Effect does have certain constraints. It is only applicable when the velocities of sound and objects are significantly less than the speed of sound in the given medium. Additionally, in the formulation of the Doppler Effect, the motion of the object and the source must occur along the same lines.
Applications of the Doppler Effect
- Estimating the speed of distant stars, planets, and other celestial bodies.
- Determining the velocities of airplanes and submarines.
- Utilized in police radar systems for measuring the speed of automobiles.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Refractive Index Formula | Lattice Energy Formula |
| Dc Voltage Drop Formula | Voltage Divider Formula |
Doppler Effect Formula FAQs
What is the Doppler Effect formula?
When is the Doppler Effect formula applicable?
Can the Doppler Effect formula be used for any type of wave?
What happens if there is a reversal in the direction of velocity in the Doppler Effect?










