
Lattice Energy Formula: Lattice energy is the energy released when two oppositely charged gaseous ions attract each other, forming an ionic solid. The total potential energy of these ionic compounds is known as lattice energy. The lattice energy per mole, denoted as U L ,can be defined as the sum of electrostatic and repulsive energy. The Born-Lande equation is utilized to calculate lattice energy.
Lattice Energy Formula
Lattice energy is the energy released when two oppositely charged gaseous ions attract each other, leading to the formation of an ionic solid. This attraction between the ions results in the release of energy, making the process exothermic. While the lattice energy can be complex Process, Coulomb's law provides a simple concept for understanding this phenomenon.
Consider the process where a metal reacts with a non-metal, typically resulting in the formation of an ionic compound through electron transfer from the metal to the non-metal. These ionic compounds often exhibit characteristics such as rigidity, brittleness, and a crystalline structure with flat surfaces arranged in a lattice.
Their resistance to deformation and high melting points, such as NaCl melting at 801°C, are attributed to the orderly organization of ions within the crystalline lattice and the potent electrostatic attractive forces between ions of opposite charges, storing energy in the structure.
Ionic Lattice Energy Formula
The formula for calculating the lattice energy of nearly any ionic solid involves a modified version of Coulomb's law and is expressed as follows:
Ionic Lattice Energy Formula
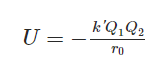
Crystalline Lattice Energy Formula
The expression for crystalline lattice energy incorporates considerations such as covalent character and electron-electron interactions within ionic solids. This approach takes into account the interplay of attraction and repulsion experienced by positive ions from those of opposite charge and ions of the same charge.
In the evaluation of lattice energy, Max Born and Alfred Landé introduced additional factors. The resulting formula, known as the Born–Landé equation, provides a means to calculate the lattice energy for a mole of a specific crystalline ionic compound. This equation is derived from the electrostatic potential of the ionic lattice, incorporating a repulsive potential energy term.
Hence, the formula is as follows:
where:
N A is Avogadro’s constant (6.022 × 10 23 )
α is the Madelung constant
e is the electron charge (1.6022 × 10 -19 C)
Z + and Z − are the cation and anion charges.
ϵ 0 is the permittivity of free space.
n is the Born Exponent.
r 0 is the closest ion distance.
Here, U L represents the equilibrium value of the lattice energy.
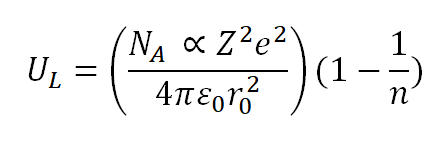
Lattice Energy Formula Solved Examples
Example 1: Calculate the lattice energy of NaCl using the Born-Lande equation.
Given α=1.74756 Z − =−1 (charge of Cl − ions) Z + =+1 (charge of Na + ion) N A =6.022×10 23 ion pairs mol − 1 C=1.60210×10 −19 C (charge on the electron) π=3.14159 ϵ 0 =8.854185×10 −12 C 2 J − 1 m − 1 r 0 =2.81×10 −10 m (sum of radii in the Born-Lande equation) n=8 (average value for Na + and Cl − ) Answer:
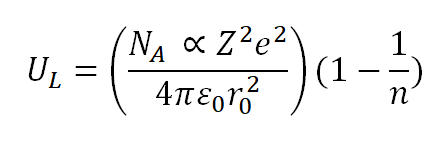
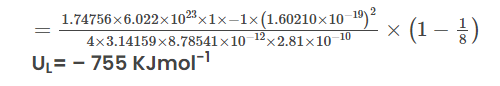
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Intensity Formula | Tangential Acceleration Formula |
| Dynamic Viscosity Formula | Uniform Circular Motion Formula |
Lattice Energy Formula FAQs
What is the Lattice Energy Formula?
What does the Lattice Energy represent?
Why is U always a positive number?
What factors affect Lattice Energy?
How is the Born-Landé equation related to Lattice Energy?










