Fluid Mechanics Formula: Important Formulas, Examples

Fluid Mechanics Formula , which can encompass both liquids and gases, is the focus of the area of physics known as fluid mechanics. It concentrates on comprehending how fluids behave both when they are stationary (fluid statics) and when they are moving (fluid dynamics). Numerous scientific, engineering, and technological applications depend heavily on fluid mechanics.

Introduction

The amount of pressure or stress applied to a solid, liquid, or gas determines its volume. When we refer to a solid or liquid's fixed volume, we mean its volume under atmospheric pressure. The distinction between solids and liquids and gases is that the volume change caused by a change in external pressure is far less pronounced for solids and liquids. In other words, compared to gases, solids and liquids are far less compressible.

Here we learn all about the the definition and formulas of terms comes under fluid mechanics

Also Read - Wave Motion Formula

Pressure

A fluid's force applied to its surroundings per unit area is known as pressure, which is a key concept in the study of fluid mechanics. It is essential to comprehending both the static and dynamic behaviour of fluids. In fluid mechanics, pressure is examined in more detail as follows:

Definition of Pressure:

Pressure (P) is defined as the force (F) exerted perpendicular to the surface of an object divided by the area (A) over which the force is distributed.

P= F/ A

Where,

P = Pressure

F = Force

A = Area

Unit of Pressure: The International System of Units (SI) uses pascals (Pa) as the unit of pressure measurement. One pascal is equal to one newton per square metre (N/m2).

Pascal’s Law

This law was given by Blaise Pascal,

Pascal's Law, sometimes referred to as Pascal's Principle, it is a fundamental tenet of fluid dynamics that states that pressure changes in a confined fluid are distributed uniformly and undiminishedly in all directions.

Definition:

According to Pascal's Law, any change in pressure imparted to a fluid confined and at rest is communicated undiminished to all of the fluid's components as well as to the container's walls.

Formula:

F=PA

Where,

F = Force Applied

P = Pressure

A = Area of cross section

Applications of Pascal’s Law

Hydraulic Systems

• Hydraulic Press
• Braking Systems
• Pneumatics
• Mechanical Engineering
• Medical Applications
• Aerospace and Aviation
• Scuba Diving
• Construction and Manufacturing

Also Read - Kinematics Formula

Streamline Flow

Laminar flow, also known as streamline flow, is a fluid flow phenomenon that lacks a single precise formula. Different equations that relate distinct fluid properties and behaviours instead are used to describe streamline flow. The following crucial calculations and ideas regarding streamline flow are listed:

Continuity Equation: The continuity equation expresses the conservation of mass in a fluid flow. It states that the mass flow rate( m _d ot ) of fluid is constant along a streamline:

= m _d ot =⍴ Av

Where,

⍴ is the fluid density,

A is the cross-sectional area, and

v is the velocity of the fluid.

Bernoulli's Equation: Bernoulli's principle describes the relationship between pressure, velocity, and elevation in streamline flow. For an incompressible, inviscid fluid (neglecting friction), Bernoulli's equation is given by:

P+ 1/ 2⍴ v ² +⍴ gh=constant

Where,

P is pressure,

⍴ is density,

v is velocity,

g is acceleration due to gravity,

and ℎ is a elevation.

Speed of Efflux: Torricelli’s Law: Torricelli's Law, also referred to as Torricelli's Theorem, defines the rate at which a fluid effluxes (extrudes) from an orifice in a container while gravity is at work. Italian scientist Evangelista Torricelli created this law in the 17th century. The law is particularly relevant when a small aperture allows a fluid to flow through it while the amount of the fluid inside the container is much higher.

The Torricelli's Law formula estimates the speed at which a fluid leaves a container as a result of gravitational forces. The formula comes from:

v= 2gh

Where,

v is the speed of efflux (velocity of fluid exiting the opening).

g is the acceleration due to gravity.

h is the vertical height of the fluid level above the opening.

Venturi-meter: The Bernoulli's equation, in particular, is used by the Venturi metre, a flow measurement device, to calculate the flow rate of a fluid. The link between the pressure differential and the flow rate is the key formula, albeit there isn't a single formula that accounts for all characteristics of the Venturi metre. The fundamental formula for calculating Venturi metres is given below:

Q= A ₁ v ₁ . A ₂ v ₂

Where.

Q= is the volumetric flow rate of the fluid.

A ₁ = is the cross-sectional area of the pipe at the inlet of the Venturi meter.

A ₂ = is the cross-sectional area of the throat (narrowest point) of the Venturi meter.

v ₁ = is the fluid velocity at the inlet of the Venturi meter.

v ₂ = is the fluid velocity at the throat of the Venturi meter.

Poiseuille's Law: The flow rate through a cylindrical pipe under streamline (laminar) conditions is described by Poiseuille's law as follows:

Q=π r ⁴ Δ P/ 8μL

Where

Q is the volumetric flow rate,

r is the radius of the pipe, Δ

ΔP is the pressure difference across the pipe,

μ is the dynamic viscosity, and

L is the length of the pipe.

Shear Stress in Streamline Flow: In streamline flow, the shear stress (

𝜏) between layers of fluid is proportional to the velocity gradient ( dv/ dy ) perpendicular to the flow direction:

𝜏=-μ ^dv / _dy

Where,

μ is dynamic viscosity and

y is the distance perpendicular to the flow direction.

Capillary Hagen-Poise:uille Equation: The Hagen-Poiseuille equation yields the volumetric flow rate for fluid flow through a cylindrical capillary under streamline conditions:

Q=π r ⁴ Δ P/ 8μL

Where, the all Poiseuille's Law definitions apply to the all terms.

Also Read - Surface Tension Formula

Viscosity

Fluids have a fundamental characteristic called viscosity that describes how they resist flowing and deforming. It is a key idea in fluid mechanics and is important for comprehending how fluids behave, particularly with regard to internal friction and their interactions with solid surfaces. The behaviour of fluids in many applications as well as phenomena like laminar and turbulent flow are all governed by viscosity.

Formula:

The ratio of shearing stress to strain rate is known as the coefficient of viscosity (pronounced "eta") for a fluid.

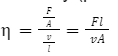
The SI unit of viscosity is poiseiulle (Pl). Its

other units are N s m-2 or Pa s.

Stokes’ Law: Stokes' Law is a fundamental principle in fluid dynamics that describes the motion of small particles suspended in a viscous fluid.

F=6𝛱𝜂 av

Where,

F= drag force

𝜂= is the dynamic viscosity of the fluid

a= radius

v= is the velocity of the particle relative to the fluid.

Reynolds Number

In fluid dynamics, the Reynolds number (Re) is a dimensionless parameter that is used to determine whether a fluid flow will be laminar or turbulent. It bears Osborne Reynolds' name because he was the physicist who first proposed the idea in the late 19th century. A key factor in comprehending how fluid flows behave under various circumstances is the Reynolds number.

The following formula is used to determine the Reynolds number:

Re=⍴ .v.L/𝜂

Where,

Re= is the Reynolds number

⍴= is the density of the fluid

v= is the velocity of the fluid relative to an object

L= length

𝜂= is the dynamic viscosity of the fluids

Surface Tension

In fluid mechanics, surface tension is a phenomena that defines how a liquid's surface behaves as a result of cohesive forces between its molecules. A liquid surface has a propensity to reduce its surface area and take on a shape that lowers the system's potential energy. A variety of natural and commercial processes depend heavily on surface tension, which has an impact on how liquids behave under various circumstances.