Indefinite Integrals Formula, Definition, Properties, Examples
Indefinite Integral: In this case, we will focus on the indefinite integral, which deals with finding antiderivatives or the general forms of functions that have a given derivative.
Girijesh Singh4 Oct, 2023
Share
In calculus, two fundamental processes are differentiation and integration. Differentiation involves finding the derivative of a function, while integration is the inverse process of differentiation. In this discussion, we will focus on an essential concept in integration known as "integrals."
Consider a function f that is differentiable over an interval I, meaning its derivative f' exists at every point within I. This leads to a fundamental question: Can we determine the original function that would yield the given f' at each point? Functions capable of producing f' as their derivative are known as antiderivatives or primitives. The mathematical formula that provides all these antiderivatives is termed the indefinite integral of the function, and the process of finding these antiderivatives is called integration. Integrals are generally categorized into two main types: Definite Integral: This type of integral is used to calculate the accumulated effect of a function over a specific interval. Indefinite Integral: In this case, we will focus on the indefinite integral, which deals with finding antiderivatives or the general forms of functions that have a given derivative. Let's delve deeper into the concept of the indefinite integral, its definition, and properties.Indefinite Integrals Definition
An indefinite integral is an integral that does not have specific upper and lower limits. In mathematical terms, if F(x) represents any antiderivative of the function f(x), then the most general antiderivative of f(x) is referred to as an indefinite integral and is denoted as: ∫f(x) dx = F(x) + C Here are some symbols, terms, and phrases along with their meanings for better understanding: ∫: The integral symbol represents the process of integration. f(x): This represents the function for which we want to find the antiderivative. dx: It indicates the variable of integration, representing the independent variable. F(x): This represents any antiderivative of the function f(x). C: The constant "C" is known as the constant of integration and can take any real value. It accounts for the fact that there can be multiple antiderivatives of a given function. This notation and concept of indefinite integrals are fundamental in calculus and are used extensively for finding antiderivatives of various functions.| Symbols/Terms/Phrases | Meaning |
| ∫ f(x) dx | Integral of f with respect to x |
| f(x) in ∫ f(x) dx | Integrand |
| x in ∫ f(x) dx | Variable of integration |
| An integral of f | A function F such that F′(x) = f (x) |
| Integration | The process of finding the integral |
| Constant of Integration | Any real number C, considered as constant function |
Also Check - Derivatives Formula
Antiderivatives or integrals of functions are not unique. There are infinitely many antiderivatives for certain functions, and they can be obtained by choosing an arbitrary constant "C" from the set of real numbers. For this reason, "C" is commonly referred to as an arbitrary constant. It serves as the parameter that allows us to obtain different antiderivatives (or integrals) of the same given function. This arbitrary constant accounts for the various possible forms of antiderivatives and is a fundamental concept in indefinite integration.Indefinite Properties
Property 1: The process of differentiation and integration are inverses of each other in the sense of the following results: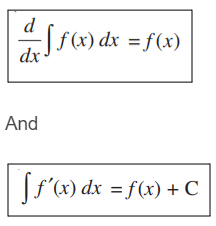
where C is any arbitrary constant.
Let us now prove this statement.
Proof: Consider a function f such that its anti-derivative is given by F, i.e.
The derivative of a function f in x is given as f’(x), so we get;
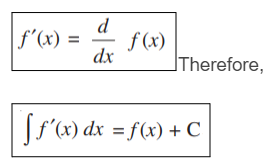Hence, proved.
Property 2:
Two indefinite integrals with the same derivative lead to the same family of curves, and so they are equivalent.
Proof: Let f and g be two functions such that
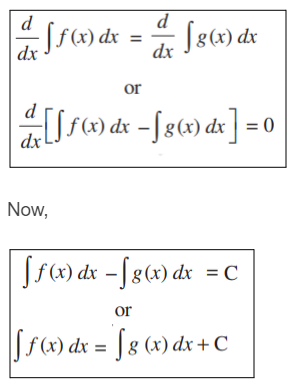where C is any real number.
From this equation, we can say that the family of the curves of [ ∫ f(x)dx + C3, C3 ∈ R] and [ ∫ g(x)dx + C2, C2 ∈ R] are the same.
Therefore, we cay say that, ∫ f(x)dx = ∫ g(x)dx
Property 3:
The integral of the sum of two functions is equal to the sum of integrals of the given functions, i.e.,
Proof: From property 1 we can say that
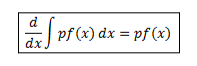Also,
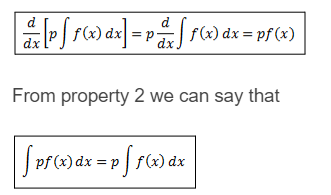
Property 5:
For a finite number of functions f1, f2…. fn and the real numbers p1, p2…pn, ∫[p1f1(x) + p2f2(x)….+pnfn(x) ]dx = p1∫f1(x)dx + p2∫f2(x)dx + ….. + pn∫fn(x)dx Indefinite Integral Formulas The list of indefinite integral formulas are- ∫ 1 dx = x + C
- ∫ a dx = ax + C
- ∫ xn dx = ((xn+1)/(n+1)) + C ; n ≠ 1
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ cosec2x dx = -cot x + C
- ∫ sec x tan x dx = sec x + C
- ∫ cosec x cot x dx = -cosec x + C
- ∫ (1/x) dx = ln |x| + C
- ∫ ex dx = ex + C
- ∫ ax dx = (ax/ln a) + C ; a > 0, a ≠ 1
Also Check - Differential Equation Formula
Indefinite Integrals Examples
Example 1:
Let's evaluate the given indefinite integral problem: ∫(6x^5 - 18x^2 + 7) dx. Solution: Given, ∫(6x^5 - 18x^2 + 7) dx Integrate the given function: ∫(6x^5 - 18x^2 + 7) dx = (6/6)x^6 - (18/3)x^3 + 7x + C After simplification, we get the solution: ∫(6x^5 - 18x^2 + 7) dx = x^6 - 6x^3 + 7x + CExample 2:
Evaluate f(x) given that f'(x) = 6x^8 - 20x^4 + x^2 + 9. Solution: Given, f'(x) = 6x^8 - 20x^4 + x^2 + 9 We know that the inverse process of differentiation is integration: f(x) = ∫f'(x) dx = ∫(6x^8 - 20x^4 + x^2 + 9) dx After integration, we obtain: f(x) = (2/3)x^9 - 4x^5 + (1/3)x^3 + 9x + CAlso Check - Vector Formula
Indefinite Integral vs Definite Integral
An indefinite integral is a mathematical function that represents the antiderivative of another function. It is typically denoted using the integral symbol, followed by a function expression, and then "dx" to indicate the variable of integration. The indefinite integral is a concise way to express the process of finding the antiderivative of a function. While the concept of indefinite integrals is similar to that of definite integrals, the two are distinct. In the context of a definite integral, specific upper and lower limits are defined to calculate the accumulated effect of a function over a specified interval. In contrast, an indefinite integral focuses on finding the general antiderivative of a function without specifying a particular interval. The difference between definite and indefinite integrals can be visually represented as shown in the figure below, highlighting their distinct characteristics and purposes.Indefinite Integrals Formula FAQs
How do you find the indefinite integral?
To find the indefinite integral of a function, you perform the process of integration or antideriviation on the function f(x). This process can be represented as:
∫f(x) dx = F(x) + C, where C is an arbitrary constant.
Suitable integration techniques and formulas are applied to obtain the antiderivative of the given function. The result of the indefinite integral is a function.
What does an indefinite integral represent?
The indefinite integral represents a family of functions, all of which have the same derivative as the original function f. It represents the set of antiderivatives of the given function.
Are indefinite integrals and antiderivatives the same?
Yes, indefinite integrals and antiderivatives refer to the same concept. When you find the indefinite integral of a function, you are essentially finding its antiderivative, which is a function that, when differentiated, gives the original function.
Do definite integrals have C?
No, definite integrals do not contain the constant "C" in their expressions. The "C" is only present in the result of an indefinite integral, representing the family of antiderivative functions.
What are the bounds of an indefinite integral?
There are no specific bounds for an indefinite integral. It deals with finding the general antiderivative of a function and does not involve specific upper and lower limits as seen in definite integrals.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.