Vector Formula, Definition, Solved Examples

Vector formulas are a collection of mathematical formulas designed to facilitate various arithmetic operations involving vectors. These formulas are particularly useful for performing calculations on individual vectors as well as for operations between two vectors. Vectors have both scalar and vector components, and vector formulas serve as valuable tools for conducting these operations in a systematic and efficient manner.

What are the List of Vector Formulas?

Vector formulas encompass a wide range of operations that can be applied to a single vector as well as operations involving two vectors. These formulas cover various aspects of vector analysis. Some formulas, such as those for direction ratios, direction cosines, vector magnitude, and unit vectors, are used to manipulate and analyze individual vectors. On the other hand, formulas for dot products, cross products, and vector projections involve operations performed between two vectors, allowing for meaningful calculations and comparisons in vector analysis.

Also Check - Matrices Formula

Triangular law of addition

If two forces Vector A and Vector B are acting in the same direction, then its resultant R will be the sum of two vectors.

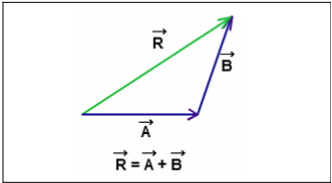
Formula for Triangular law addition:

Parallelogram law of addition

When two forces, Vector A and Vector B, are represented by the adjacent sides of a parallelogram, the resultant of these forces is represented by the diagonal of the parallelogram that originates from the same point as the two forces. This is a fundamental concept in vector addition, where the resultant force is determined by the geometric properties of the parallelogram formed by the vectors. The diagonal of the parallelogram represents the direction and magnitude of the resultant force when the two vectors are added together.

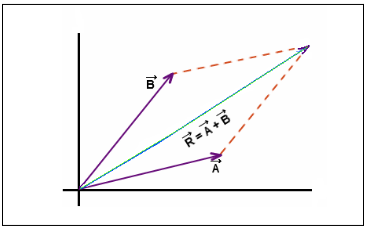
Formula for parallelogram law addition:

Also Check - Determinants Formula

Vector Subtraction

When two forces, Vector A and Vector B, are acting in opposite directions, their resultant force R can be represented by the difference between the two vectors. This means that you subtract Vector B from Vector A to find the resultant force R. The direction of the resultant will be determined by the direction of the larger vector, and its magnitude will be the difference in magnitudes between Vector A and Vector B. This concept is commonly used in physics and engineering to determine the net effect of forces acting in opposite directions.

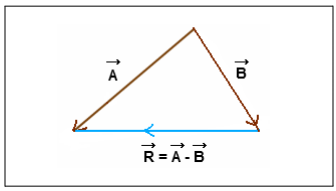
Formula for vector subtraction:

Also Check - Derivatives Formula

Vector Formulas Examples

Solved examples of vectors:

(a) The vector from (2, -7, 0) to (1, -3, -5):

To construct this vector, subtract the coordinates of the starting point from the ending point:

{1 - 2, (-3) - (-7), (-5) - 0} = {-1, 4, -5}

(b) The vector from (1, -3, -5) to (2, -7, 0):

Similarly, subtract the coordinates of the starting point from the ending point:

{2 - 1, (-7) - (-3), 0 - (-5)} = {1, -4, 5}

Notice that the only difference between the first two vectors is the signs are all opposite. This difference indicates that the two vectors point in opposite directions.

(c) The position vector for (-90, 4):

The position vector of a point is a vector with the point's coordinates as its components:

Position vector = (-90, 4)