
Tangential Acceleration Formula: Tangential acceleration refers to the change in tangential velocity in the rotational movement of an object. It operates along the tangent at the point of motion for the object. Similarly, the tangential velocity also aligns with this direction in circular motion. This type of acceleration is present exclusively when an object follows a circular path. It is positive when the object is accelerating, negative during deceleration, and zero when the object maintains a constant speed in its orbit.
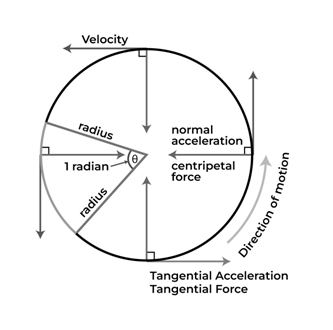
Tangential Acceleration Definition
Tangential acceleration shares similarities with linear acceleration, but it operates exclusively in one direction, particularly in the context of circular motion. It represents the rate at which a particle's tangential velocity changes within a circular orbit, consistently aligning with the tangent of the object's path.
Straight-line linear acceleration, tangential acceleration is specifically relevant when an object traverses a circular path. When an object moves in a straight line, it undergoes linear acceleration, but this is distinct from the circular motion governed by tangential acceleration.
Tangential Acceleration
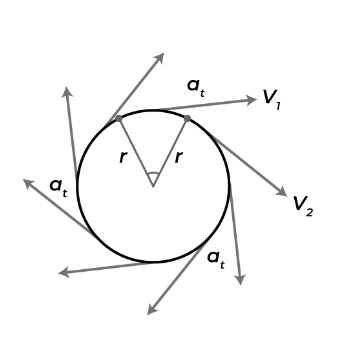
Consider a scenario where a car is navigating a curve on the road, representing tangential acceleration as it accelerates in alignment with the bend. For a deeper understanding of acceleration, explore the following information: Tangential Acceleration: Unveiling the Formula Tangential acceleration, represented by the symbol a t , shares the same unit of measurement as linear acceleration, denoted in meters per square second (m/s²). Its dimensional formula is expressed as [M⁰L¹T⁻²].
Tangential Acceleration Formula
The formula for tangential acceleration is the product of the radius of a circular path and the angular acceleration of the rotating object:
a t =rα
Where: a t is the tangential acceleration, r is the radius of the circular path, α is the angular acceleration.
This formula establishes the relationship between tangential acceleration and angular acceleration. Now, expressing the formula in terms of angular velocity ( ω) and time ( t):
a t =r( ω/t )
Where:
- a t is the tangential acceleration,
- ω is the angular velocity,
- t is the time taken.
Similarly, in terms of angular displacement ( θ) and time ( t):
a t =r( θ /t 2 )
Where:
- a t is the tangential acceleration,
- θ is the angular displacement or angle of rotation,
- t is the time taken.
These formulations provide a comprehensive understanding of tangential acceleration and its various representations in different contexts.
Different Scenarios Based on Tangential Acceleration:
Positive Tangential Acceleration ( a t >0):
- The object experiences accelerated motion.
- The magnitude of velocity increases over time.
Negative Tangential Acceleration ( a t <0):
- The object undergoes deceleration or moves slowly.
- The magnitude of velocity decreases with time.
Zero Tangential Acceleration ( a t =0):
- The object maintains uniform motion.
- The magnitude of velocity remains constant.
Tangential Acceleration Formula Solved Examples
Example 1: Find the tangential acceleration when an object is moving in a circular path with a radius of 8 meters and an angular acceleration of 3.5 rad/s².
Solution: Given: r=8 α=3.5
Using the formula: a t =rα
a t =8×3.5
a t =28m/s 2
Example 2: Determine the tangential acceleration for an object in circular motion with a radius of 15 meters and an angular acceleration of 1.2 rad/s².
Solution: Given: r=15 α=1.2
Using the formula: a t =rα
a t =15×1.2
a t =18m/s 2
These examples illustrate the application of the tangential acceleration formula in different scenarios of circular motion.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Physics knowledge. and build a strong foundation.
| Related Links | |
| Bulk Modulus Formula | Cop Formula |
| Angular Speed Formula | Mechanical Advantage Formula |
Tangential Acceleration Formula FAQs
What does the tangential acceleration formula represent?
How is tangential acceleration measured?
What does a positive tangential acceleration indicate?
What does a negative tangential acceleration indicate?










