The
Law of Sines
, which is also known as the Sine Law, Sine Rule, and Sine Formula. This mathematical principle is used in trigonometry to relate the angles and sides of a non-right triangle, known as an oblique triangle. Here's a more detailed explanation:
The Law of Sines states that, for any triangle (not just right triangles), the ratio of the length of a side to the sine of its opposite angle is constant. In mathematical terms, if you have a triangle with sides A, B, and C, and opposite angles A, B, and C:
Law of Sines Definition
The Law of Sines, as you've described, holds for all three sides of a triangle irrespective of their lengths and the angles in the triangle. In a more general form, it can be written as:
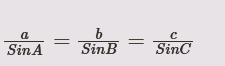
In a triangle with sides A, B, and C, and opposite angles A, B, and C, respectively:
This equation states that the ratio of the length of any side to the sine of the angle opposite that side is a constant value, and this constant is typically denoted as k in mathematical discussions. It's a fundamental principle in trigonometry that applies to all triangles, whether they are acute, obtuse, or right-angled.
This law is a powerful tool for solving various types of problems involving triangles, helping find missing side lengths or angles when certain information is known. It's particularly useful in cases where you have either two angles and one side or two sides and one non-included angle. The Law of Sines is a valuable addition to the toolkit of trigonometric principles used in geometry and trigonometry.
(Sin A/a) = (Sin B/b) = (Sin C/c)
This is just a rearrangement of the Law of Sines. In these forms, you can solve for the angles
A and B when you know the lengths of sides a and b and the angle C. It's a useful way to find missing angle measures in a triangle, especially in situations where you have information about two sides and a non-included angle. This flexibility in using the Law of Sines to solve for different variables in a triangle is one of its key features, making it a valuable tool in trigonometry.
Law of Sines Proof
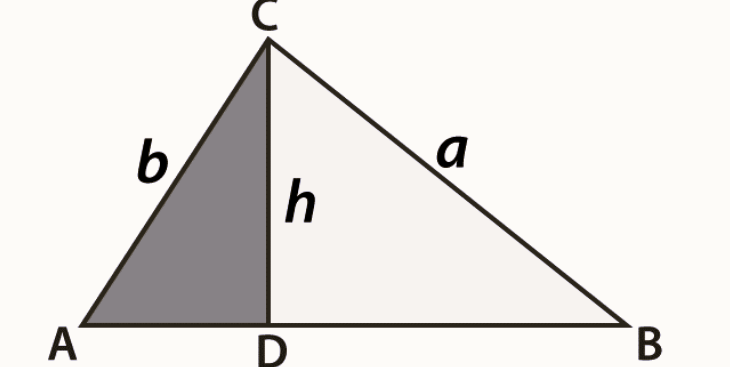
Given:
△ABC, AB = c, BC = a and AC = b.
Construction:
Draw a perpendicular, CD ⊥ AB. Then CD = h is the height of the triangle. “h” separates the △ ABC in two right-angled triangles, △CDA and △CDB.
To Show:
a / b = Sin A / Sin B
Proof:
In the △CDA,
Sin A= h/b
And in △CDB,
Sin B = h/a
Therefore, Sin A / Sin B = (h / b) / (h / a) = a/b
And we proved it.
Similarly, we can prove, Sin B/ Sin C= b / c and so on for any pair of angles and their opposite sides.
Sine Formula
|
a / Sin A= b/ Sin B= c / Sin C
|
|
a: b: c = Sin A: Sin B: Sin C
|
|
a / b = Sin A / Sin B
|
|
b / c = Sin B / Sin C
|
It denotes that if we divide side a by the Sine of ∠A, it is equal to the division of side b by the Sine of∠ B and also equal to the division of side c by Sine of ∠C (Or) The sides of a triangle are to one another in the same ratio as the sines of their opposite angles.
Here, Sin A is a number and a is the length.
Also Check –
Probability Formula
Sine Law Applications in Real Life
The Law of Sines (Sine Law) is a fundamental trigonometric concept used in a wide range of applications. Here are some of its practical applications:
-
Navigation and Surveying:
The Law of Sines is used in navigation and surveying to determine distances, positions, and angles. Navigators and surveyors use it to find distances or angles between known points or landmarks.
-
Astronomy:
Astronomers use the Law of Sines to determine the distances and sizes of celestial objects, as well as to calculate the positions of stars and planets.
-
Physics:
In physics, it's applied in problems involving the motion of objects, including projectiles and waves. It's used to calculate angles of deflection, trajectories, and other motion-related parameters.
-
Engineering:
Engineers use the Law of Sines in various fields, such as civil engineering for designing structures, electrical engineering for antenna design, and mechanical engineering for analyzing forces and motion.
-
Architecture:
Architects use trigonometry, including the Law of Sines, to calculate angles and dimensions when designing buildings and structures.
-
Geography:
In geography, the Law of Sines is applied to determine the locations of points on the Earth's surface based on the angles and distances between them.
-
Computer Graphics:
The Law of Sines is used in computer graphics to model and animate the motion of objects, the shape of 3D models, and the rendering of images.
-
Artillery and Ballistics:
The military uses the Law of Sines for calculating firing solutions, including projectile trajectories, distances, and angles in artillery and ballistics.
-
Trilateration:
In geodesy and GPS technology, trilateration involves using the Law of Sines to determine the position of a point by measuring distances to known reference points.
-
Air and Space Navigation:
Pilots and astronauts use the Law of Sines for navigation, especially in non-Euclidean environments like the surface of the Earth or other celestial bodies.
-
Architecture and Construction:
Architects and construction professionals use trigonometric principles, including the Law of Sines, to ensure that buildings and structures are properly designed and constructed with accurate angles and measurements.
-
Geometry and Trigonometry Education:
The Law of Sines is an important topic in geometry and trigonometry courses, helping students understand and apply trigonometric principles.
In summary, the Law of Sines has a wide range of practical applications across various fields, from science and engineering to navigation and construction, where it is used to solve problems related to triangles, angles, distances, and positions.
Also Check –
Introduction to Euclid Formula
Law of Sines Uses
the Law of Sines can be applied and the concept of the ambiguous case. Let's delve into these concepts in a bit more detail:
ASA (Angle-Side-Angle) Criteria:
When you know two angles and the included side of a triangle, you can use the Law of Sines to find the lengths of the other sides. This is because ASA is a sufficient condition to prove the congruence of triangles, meaning you can uniquely determine the triangle based on this information.
AAS (Angle-Angle-Side) Criteria:
If you have two angles and a non-included side of a triangle, the Law of Sines can be used to find the lengths of the other sides. Again, AAS is a sufficient condition to establish the congruence of triangles, ensuring a unique solution.
Ambiguous Case
When you have two sides and the angle opposite one of those sides (SSA), the situation becomes ambiguous. There are three possible scenarios:
No Such Triangle: If the given information doesn't satisfy the triangle inequality theorem (i.e., the sum of the lengths of any two sides must be greater than or equal to the length of the third side), then there is no triangle that satisfies the conditions.
Two Different Triangles: If the given information allows for two different triangles to be formed, it's called the ambiguous case. This typically happens when the angle opposite the known side is acute, and you can construct either an acute-angled or obtuse-angled triangle.
Exactly One Such Triangle: If the angle opposite the known side is obtuse, you can often form only one triangle that satisfies the conditions.
The ambiguous case is a situation where the Law of Sines does not guarantee a unique solution, and additional information may be needed to determine the triangle's characteristics. It highlights the importance of understanding the triangle inequality theorem and carefully considering the given information to determine the number and nature of possible triangles.
Also Check –
Triangles Formula
Law of Sines and Cosines
|
Law of sines
|
Law of cosines
|
It is used when we are given with:
-
two angles and one side, or
-
two sides and a non-included angle
|
It is used when we are given with:
-
three sides, or
-
two sides and the included angle.
|
|
If a, b and c are the sides and A, B and C are the angles of a triangle, then sine rule is given by:
a/SinA = b/SinB = c/SinC
|
If a, b and c are the sides and A, B and C are the angles of a triangle, then cosine rule is given by:
a
2
= b
2
+ c
2
− 2bc cos A
b
2
= a
2
+ c
2
− 2ac cos B
c
2
= a
2
+ b
2
− 2ab cos C
|
