Differentiation

Differentiation

Sep 07, 2022, 16:45 IST

In calculus, differentiation is one of two important concepts besides integration. In mathematics, differentiation is a method of finding the derivative of a function. Differentiation is a process in mathematics where we find the instantaneous rate of change of a function based on one of its variables.

The most common example is the change in displacement speed with respect to time, that is known as velocity. The Anti-differentiation is the opposite of finding a derivative. If x is a variable and y is another variable, then the rate of change of x with respect to y is dy/dx. This is a general expression for the derivative of a function and is represented as f'(x) = dy/dx, where y = f(x) is any function.

What is Differentiation in mathematics?

In mathematics, a differentiation can be defined as the derivative of a function with respect to the independent variable. Differentiation in calculus can be used to measure a function per unit change in the independent variable.

Let y = f(x) be a function of x. Therefore, the rate of change of y per unit change in x is dy / dx .

If the function f(x) undergoes an infinitesimal change of h near any point x, then the derivative of the function is:

Lim f(x + h) − f(x)/ h

where h tends to 0

What is Differentiation in Physics?

Differentiation in physics is similar to differentiation in Mathematics. The concepts from differentiation in Maths are used in physics too.

Derivative of Function As Limits

If we are given with real-valued function (f) and x is a point in its domain of definition, then the derivative of a function, f, is: f'(a) = limh→0[f(x + h) – f(x)]/h

Notation

When a function is represented by y = f(x), the derivative is indicated by the following notations.

• D[f(x)] or D(y) is called Euler’s notation.
• F’(x) is called Lagrange’s notation.
• dy/dx is called Leibniz’s notation.

Linear and Non-Linear Functions

Functions are generally classified into two functions under Calculus, namely:

1. Linear functions
2. Non-linear functions

A linear function always varies at a constant rate through its domain. Therefore, the total rate of change of the function is the same as the rate of change at any point. However, the rate of change of the function varies from point to point in the case of non-linear functions. The nature of the variation is based on the nature of the function. The rate of change of a function at a particular point is the derivative of that particular function.

Important formulas in differentiation

Some of the important differentiation formulas are given below. We have to consider f(x) as a function and f’(x) as the derivative of the function:

1. If f(x) = tan(x) then f’(x) = sec ² x.
2. If f(x) = cos(x) then f’(x) = −sin x.
3. If f(x) = sin(x) then f’(x) = cos x.
4. If f(x) = In(x) then f’(x) = 1/x.
5. If f(x) = e ^x then f’(x) = e ^x .
6. If f(x) = x ⁿ then f’(x) = nx ^n-1 where n is any fraction or integer.
7. If f(x) = k then f’(x) = 0 and here k is a constant.

Rules of differentiation

Some basic differentiation rules that you need to be followed are as follows:

• Sum and Difference Rule
• Product Rule
• Quotient Rule
• Chain Rule

Sum or Difference Rule

If the function is either sum or difference of two functions, then the derivative of the functions is sum or difference of the given functions, i.e.,

If f(x) = u(x) ± v(x)

then, f'(x) = u'(x) ± v'(x)

Product Rule

As per the product rule, if the function f(x) is a product of two functions u(x) and v(x), the derivative of the function is,

f'(x) = u'(x) x v(x) + u(x) x v'(x)

Quotient rule

If function f(x) is in the form of two functions i.e., [u(x)] / [v(x)], the derivative of the function is: f(x) = u(x) / v(x)

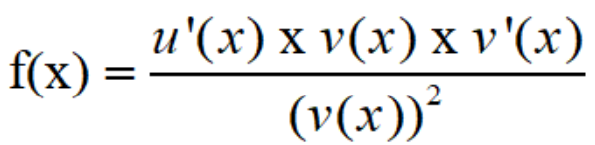
Chain Rule

If the function y = f(x) = g(u) and if u = h(x), then the chain rule for differentiation is defined as,

dy/dx = dy/du x du/dx

This plays a important role in the method of substitution that helps to perform the differentiation of composite functions.

Solved Examples

Q1. Differentiate f(x) = 6x ³ – 9x + 4 with respect to x.

Ans. Given: f(x) = 6x ³ – 9x + 4

On differentiating both the sides w.r.t x, we get;

f'(x) = (3)(6)x ² – 9

f'(x) = 18x ² – 9

This is the final answer.

Q2. Differentiate y = x(3x ² – 9)

Ans. Given, y = x(3x ² – 9)

y = 3x ³ – 9x

On differentiating both the sides we get,

dy/dx = 9x ² – 9

This is the final answer.

Frequently Asked Question (FAQs)

Q1. What is the use of Differentiation in everyday life?

Ans. To determine the temperature variation. Also check the speed or distance covered, such as miles per hour, kilometres per hour, etc.

Q2. What are the basic rules of differentiation?

Ans. The important rules of differentiation are:

• Sum and Difference Rule
• Product Rule
• Quotient Rule
• Chain Rule

Q3. What are the six derivative rules?

Ans. The six derivative rules are:

1. d/dx (cos x) = - sin x
2. d/dx (sin x) = cos x
3. d/dx (tan x) = sec ² x
4. d/dx (cosec x) = - cosec x cot x
5. d/dx (sec x) = sec x tan x
6. d/dx (cot x) = - cosec ² x

Q4. What is the differentiation of 0?

Ans. 0 has no derivative. The derivative measures the rate of change. 0 does not change, so it can't have a rate of change.

Q5. What is the derivative of XY?

Ans. The derivative of is: x d y/d x + y .