NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 Determinants

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 Determinants

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 Determinants is prepared by academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter 4. Given below is step by step solutions of all questions given in NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6.

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 Overview

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 Determinants is prepared by our experts to help students understand the concepts of the chapter better.

Students can solve these questions before their examinations these questions will help them to understand the concepts better and by doing these questions students can easily ace their examinations.

Checkout Class 12th Books from PW Store

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6 PDF

To assist students in comprehending and applying the concepts covered in the chapter, the Physics Wallah team has created comprehensive solutions for NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6. These questions are meant to aid students in understanding explanations.

By following this link, you can download the NCERT Solutions for Class 12 Maths, Chapter 4 PDF:

NCERT Solutions Class 12 Maths Chapter 4 PDF Download Link

Checkout Class 12th Sample Papers from PW Store

NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6

Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 4 Exercise 4.6

Examine the consistency of the system of equations in Exercises 1 to 3.

Question 1 .

x + 2 y = 2

2 x + 3 y = 3

Solution : Matrix form of given equations is AX = B

∴ A is non-singular.

Therefore, A ⁻¹ exists.

Hence, the given system of equations is consistent.

Question 2.

2 x − y = 5

x + y = 4

Solution : Matrix form of given equations is AX = B

∴ A is non-singular.

Therefore, A ⁻¹ exists.

Hence, the given system of equations is consistent.

Question 3.

x + 3 y = 5

2 x + 6 y = 8

Solution : Matrix form of given equations is AX = B

∴ A is a singular matrix.

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Examine the consistency of the system of equations in Exercises 4 to 6.

Question 4.

x + y + z = 1

2 x + 3 y + 2 z = 2

ax + ay + 2 az = 4

Solution : Matrix form of given equations is AX = B

∴ A is non-singular.

Therefore, A ⁻¹ exists.

Hence, the given system of equations is consistent.

Question 5.

3 x − y − 2z = 2

2 y − z = −1

3 x − 5 y = 3

Solution : Matrix form of given equations is AX = B

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Question 6.

5 x − y + 4 z = 5

2 x + 3 y + 5 z = 2

5 x − 2 y + 6 z = −1

Solution : Matrix form of given equations is AX = B

∴ A is non-singular.

Therefore, A ⁻¹ exists.

Hence, the given system of equations is consistent.

Solve the system of linear equations, using matrix method, in Exercise 7 to 10.

Question 7.

5x + 2y =4

7x + 3y = 5

Solution : Matrix form of given equations is AX = B

Question 8.

2x - y = - 2

3x + 4y = 3

Solution : Matrix form of given equations is AX = B

Question 9.

4x - 3y = 3

3x - 5y = 7

Solution : Matrix form of given equations is AX = B

Question 10.

5 x + 2 y = 3

3 x + 2 y = 5

Solution : Matrix form of given equations is AX = B

Thus, A is non-singular. Therefore, its inverse exists.

Solve the system of linear equations, using matrix method, in Exercise 11 to 14.

Question 11.

Solution : Matrix form of given equations is AX = B

Question 12.

x − y + z = 4

2 x + y − 3 z = 0

x + y + z = 2

Solution : Matrix form of given equations is AX = B

Question 13.

2 x + 3 y + 3 z = 5

x − 2 y + z = −4

3 x − y − 2 z = 3

Solution : Matrix form of given equations is AX = B

Question 14.

x − y + 2 z = 7

3 x + 4 y − 5 z = −5

2 x − y + 3 z = 12

Solution : Matrix form of given equations is AX = B

Question 15. If A = 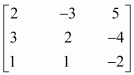find A ⁻¹ . Using A ⁻¹ solve the system of equations

Solution :

Question 16. The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ` 60. The cost of 2 kg onion, 4 kg wheat and 2 kg rice is ` 90. The cost of 6 kg onion, 2 k wheat and 3 kg rice is ` 70. Find cost of each item per kg by matrix method.

Solution :

Let the cost of onions, wheat, and rice per kg be Rs x , Rs y ,and Rs z respectively.

Then, the given situation can be represented by a system of equations as:

4x + 3y + 2z = 60

2x + 4y + 6z = 90

6x + 2y + 3z = 70

This system of equations can be written in the form of AX = B , where

Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.