NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
Ananya Gupta31 Jul, 2024
Share
NCERT Solutions for Class 9 Maths Chapter 12: Here, we provided the NCERT Solutions for Class 9 Maths Chapter 12 on Heron's Formula a key topic in geometry. This chapter focuses on calculating the area of a triangle when the lengths of all three sides are known. Heron's Formula provides a method to determine the area based on these side lengths without needing the height.
Students will learn how to use the semi-perimeter of the triangle, along with the side lengths, to find the area efficiently. These solutions are designed to help students grasp the concept thoroughly, practice problem-solving techniques and build confidence in handling geometric problems. By working through these solutions students can enhance their understanding of triangle geometry, improve their ability to solve related problems and perform better in their exams.NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula Overview
NCERT Solutions for Class 9 Maths Chapter 12 on Heron's Formula, prepared by subject experts from Physics Wallah provide a detailed overview of this important topic. By using these solutions, students can easily grasp the concept of Heron's Formula and its application. The clear explanations and step-by-step methods help in understanding the process of finding the semi-perimeter and applying the formula to solve various problems. This guidance ensures that students can confidently tackle geometric problems involving triangles and improve their overall performance in mathematics.NCERT Solutions for Class 9 Maths Chapter 12 PDF
The PDF link for the NCERT Solutions for Class 9 Maths Chapter 12 which covers Heron's Formula, is available below. This resource provides detailed solutions and explanations on how to apply Heron's Formula to find the area of a triangle when the side lengths are known. By accessing this PDF students can benefit from structured guidance and clear examples to enhance their understanding of the topic and effectively solve related problems.NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula PDF
NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
Below we have provided NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula:NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.1 (Page No: 202)
1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
Given, Side of the signal board = a Perimeter of the signal board = 3a = 180 cm ∴ a = 60 cm Semi perimeter of the signal board (s) = 3a/2 By using Heron’s formula, Area of the triangular signal board will be =
2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of ₹5000 per m 2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
Solution:
The sides of the triangle ABC are 122 m, 22 m and 120 m respectively. Now, the perimeter will be (122+22+120) = 264 m Also, the semi perimeter (s) = 264/2 = 132 m Using Heron’s formula, Area of the triangle =
=1320 m
2
We know that the rent of advertising per year = ₹ 5000 per m
2
∴ The rent of one wall for 3 months = Rs. (1320×5000×3)/12 = Rs. 1650000
3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.
Solution:
It is given that the sides of the wall as 15 m, 11 m and 6 m. So, the semi perimeter of triangular wall (s) = (15+11+6)/2 m = 16 m Using Heron’s formula, Area of the message =
= √[16(16-15)(16-11) (16-6)] m
2
= √[16×1×5×10] m
2
= √800 m
2
= 20√2 m
2
4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm.
Solution:
Assume the third side of the triangle to be “x”. Now, the three sides of the triangle are 18 cm, 10 cm, and “x” cm It is given that the perimeter of the triangle = 42cm So, x = 42-(18+10) cm = 14 cm ∴ The semi perimeter of triangle = 42/2 = 21 cm Using Heron’s formula, Area of the triangle, =
= √[21(21-18)(21-10)(21-14)] cm
2
= √[21×3×11×7] m
2
= 21√11 cm
2
5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.
Solution:
The ratio of the sides of the triangle are given as 12 : 17 : 25 Now, let the common ratio between the sides of the triangle be “x” ∴ The sides are 12x, 17x and 25x It is also given that the perimeter of the triangle = 540 cm 12x+17x+25x = 540 cm 54x = 540cm So, x = 10 Now, the sides of triangle are 120 cm, 170 cm, 250 cm. So, the semi perimeter of the triangle (s) = 540/2 = 270 cm Using Heron’s formula, Area of the triangle
= 9000 cm
2
6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
First, let the third side be x. It is given that the length of the equal sides is 12 cm and its perimeter is 30 cm. So, 30 = 12+12+x ∴ The length of the third side = 6 cm Thus, the semi perimeter of the isosceles triangle (s) = 30/2 cm = 15 cm Using Heron’s formula, Area of the triangle =
= √[15(15-12)(15-12)(15-6)] cm
2
= √[15×3×3×9] cm
2
= 9√15 cm
2
NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.2 (Page No: 206)
1. A park, in the shape of a quadrilateral ABCD, has C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution:
First, construct a quadrilateral ABCD and join BD. We know that C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m The diagram is:
Now, apply Pythagoras theorem in ΔBCD
BD
2
= BC
2
+CD
2
⇒ BD
2
= 12
2
+5
2
⇒ BD
2
= 169
⇒ BD = 13 m
Now, the area of ΔBCD = (½ ×12×5) = 30 m
2
The semi perimeter of ΔABD
(s) = (perimeter/2)
= (8+9+13)/2 m
= 30/2 m = 15 m
Using Heron’s formula,
Area of ΔABD
= 6√35 m
2
= 35.5 m
2
(approximately)
∴ The area of quadrilateral ABCD = Area of ΔBCD+Area of ΔABD
= 30 m
2
+35.5m
2
= 65.5 m
2
2. Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
First, construct a diagram with the given parameter.
Now, apply Pythagorean theorem in ΔABC,
AC
2
= AB
2
+BC
2
⇒ 5
2
= 3
2
+4
2
⇒ 25 = 25
Thus, it can be concluded that ΔABC is a right angled at B.
So, area of ΔBCD = (½ ×3×4) = 6 cm
2
The semi perimeter of ΔACD (s) = (perimeter/2) = (5+5+4)/2 cm = 14/2 cm = 7 m
Now, using Heron’s formula,
Area of ΔACD
= 2√21 cm
2
= 9.17 cm
2
(approximately)
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD = 6 cm
2
+9.17 cm
2
= 15.17 cm
2
3. Radha made a picture of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.
Solution:
For the triangle I section:
It is an isosceles triangle and the sides are 5 cm, 1 cm and 5 cm
Perimeter = 5+5+1 = 11 cm
So, semi perimeter = 11/2 cm = 5.5 cm
Using Heron’s formula,
Area = √[s(s-a)(s-b)(s-c)]
= √[5.5(5.5- 5)(5.5-5)(5.5-1)] cm
2
= √[5.5×0.5×0.5×4.5] cm
2
= 0.75√11 cm
2
= 0.75 × 3.317cm
2
= 2.488cm
2
(approx)
For the quadrilateral II section:
This quadrilateral is a rectangle with length and breadth as 6.5 cm and 1 cm respectively. ∴ Area = 6.5×1 cm 2 =6.5 cm 2For the quadrilateral III section:
It is a trapezoid with 2 sides as 1 cm each and the third side as 2 cm. Area of the trapezoid = Area of the parallelogram + Area of the equilateral triangle The perpendicular height of the parallelogram will be
= 0.86 cm
And, the area of the equilateral triangle will be (√3/4×a
2
) = 0.43
∴ Area of the trapezoid = 0.86+0.43 = 1.3 cm
2
(approximately).
For triangle IV and V:
These triangles are 2 congruent right angled triangles having the base as 6 cm and height 1.5 cm Area triangles IV and V = 2×(½×6×1.5) cm 2 = 9 cm 2 So, the total area of the paper used = (2.488+6.5+1.3+9) cm 2 = 19.3 cm 24. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:
Given, It is given that the parallelogram and triangle have equal areas. The sides of the triangle are given as 26 cm, 28 cm and 30 cm. So, the perimeter = 26+28+30 = 84 cm And its semi perimeter = 84/2 cm = 42 cm Now, by using Heron’s formula, area of the triangle =
= √[42(42-26)(42-28)(42-30)] cm
2
= √[42×16×14×12] cm
2
= 336 cm
2
Now, let the height of parallelogram be h.
As the area of parallelogram = area of the triangle,
28 cm× h = 336 cm
2
∴ h = 336/28 cm
So, the height of the parallelogram is 12 cm.
5. A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution:
Draw a rhombus-shaped field first with the vertices as ABCD. The diagonal AC divides the rhombus into two congruent triangles which are having equal areas. The diagram is as follows.
Consider the triangle BCD,
Its semi-perimeter = (48 + 30 + 30)/2 m = 54 m
Using Heron’s formula,
Area of the ΔBCD =
= 432 m
2
∴ Area of field = 2 × area of the ΔBCD = (2 × 432) m
2
= 864 m
2
Thus, the area of the grass field that each cow will be getting = (864/18) m
2
= 48 m
2
6. An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig.12.16), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
Solution:
For each triangular piece, The semi perimeter will be s = (50+50+20)/2 cm = 120/2 cm = 60cm Using Heron’s formula, Area of the triangular piece =
= √[60(60-50)(60-50)(60-20)] cm
2
= √[60×10×10×40] cm
2
= 200√6 cm
2
∴ The area of all the triangular pieces = 5 × 200√6 cm
2
= 1000√6 cm
2
7. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. 12.17. How much paper of each shade has been used in it?
Solution:
As the kite is in the shape of a square, its area will be A = (½)×(diagonal) 2 Area of the kite = (½)×32×32 = 512 cm 2. The area of shade I = Area of shade II 512/2 cm 2 = 256 cm 2 So, the total area of the paper that is required in each shade = 256 cm 2 For the triangle section (III), The sides are given as 6 cm, 6 cm and 8 cm Now, the semi perimeter of this isosceles triangle = (6+6+8)/2 cm = 10 cm By using Heron’s formula, the area of the III triangular piece will be =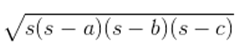
= √[10(10-6)(10-6)(10-8)] cm
2
= √(10×4 ×4×2) cm
2
= 8√5 cm
2
= 17.92 cm
2
(approx.)
8. A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50p per cm 2 .
Solution:
The semi perimeter of the each triangular shape = (28+9+35)/2 cm = 36 cm By using Heron’s formula, The area of each triangular shape will be
= 36√6 cm
2
= 88.2 cm
2
Now, the total area of 16 tiles = 16×88.2 cm
2
= 1411.2 cm
2
It is given that the polishing cost of tiles = 50 paise/cm
2
∴ The total polishing cost of the tiles = Rs. (1411.2×0.5) = Rs. 705.6
9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
First, draw a line segment BE parallel to the line AD. Then, from B, draw a perpendicular on the line segment CD.
Now, it can be seen that the quadrilateral ABED is a parallelogram. So,
AB = ED = 10 m
AD = BE = 13 m
EC = 25-ED = 25-10 = 15 m
Now, consider the triangle BEC,
Its semi perimeter (s) = (13+14+15)/2 = 21 m
By using Heron’s formula,
Area of ΔBEC =
= 84 m
2
We also know that the area of ΔBEC = (½)×CE×BF
84 cm
2
= (½)×15×BF
BF = (168/15) cm = 11.2 cm
So, the total area of ABED will be BF×DE i.e. 11.2×10 = 112 m
2
∴ Area of the field = 84+112 = 196 m
2
Benefits of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
- Clear Explanation of Concepts : The solutions provide a thorough explanation of Heron's Formula including step-by-step procedures for calculating the area of a triangle using its side lengths. This helps students grasp the underlying principles more effectively.
- Practical Problem-Solving : By working through the provided exercises students can practice applying Heron's Formula to various problems, reinforcing their problem-solving skills and understanding of geometric concepts.
- Enhanced Exam Preparation : Familiarity with the types of problems and solution methods included in the chapter helps students prepare for exams by building confidence and improving their ability to tackle similar questions.
- Comprehensive Coverage : The solutions cover a range of problems from basic to more complex, ensuring that students get a well-rounded understanding of how to use Heron's Formula in different contexts.
NCERT Solutions for Class 9 Maths Chapter 12 FAQs
How do you calculate the semi-perimeter?
When can Heron's Formula be used?
Can Heron's Formula be used for any type of triangle?
What if one of the side lengths is not known?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
