Rydberg Formula: Definition, Equation, Solved Examples

The Rydberg formula serves as a mathematical tool for determining the wavelength of light emitted during the transition of an electron between energy levels within an atom. As an electron shifts from one atomic orbital to another, its energy undergoes a change. When this electron transitions from an orbital with higher energy to one with lower energy, it emits a photon of light. Conversely, when an electron moves from a lower energy state to a higher one, the atom absorbs a photon of light. The Rydberg formula applies to the spectral analysis of various elements and is expressed as follows:

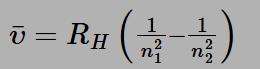
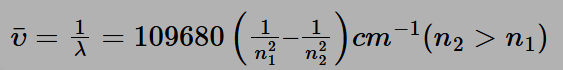
Where:

n1 and n2  are integers, with n2 always being greater than n1

R is a constant known as the Rydberg constant, typically denoted as:

R =109677.57 cm −1

This value is recognized as one of the most accurately known physical constants.

Johannes Rydberg, a Swedish physicist, conducted experiments to establish a mathematical relationship between the spectral lines of specific elements, noticing integer relationships between successive wavenumbers of these lines.

In 1888, he initially proposed this relationship empirically, and it was later theoretically explained by Niels Bohr in 1913, employing an early version of quantum mechanics. The formula directly provides the equations necessary for calculating the wavelengths within the spectral series of hydrogen.

Also Check - Gibbs Free Energy Formula

Rydberg Formula Solved Examples

Example 1: In the Paschen series, where energy levels are identified by the numbers n 1 ​ and n 2 ​ , we have n 1 ​ =3 and n 2 ​ =4,5,…. As a result, the transition represented by the second line in the Paschen series occurs when n 1 ​ =3 and n 2 ​ =5.

Replace the values mentioned earlier in the equation.

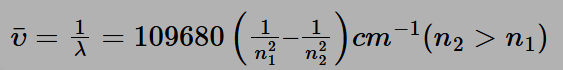
The value of ν is 7.799 x 10^3 cm^-1, and this corresponds to a wavelength ( λ) of 1.282 x 10^-4 cm, which is equivalent to 1282 nanometers (nm). This wavelength falls within the near-infrared region of the electromagnetic spectrum.

Also Check - Percentage Yield Formula

Example 2: Within the Balmer series, if we take n 1 ​ =2 and n 2 ​ =3,4,…, we can determine the characteristics of the transition corresponding to the third line in the Balmer series when n 1 ​ =2 and n 2 ​ =4.

Substituting these values into the equation provides the following results:

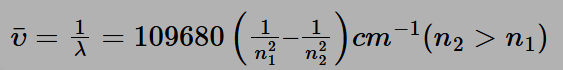
The value of  ν is calculated to be 5.43 x 10^3 cm^-1, which corresponds to a wavelength (  λ) of 1.844 x 10^-4 cm or 1844 nm. This wavelength falls into the near-infrared part of the electromagnetic spectrum.

Example 3: In the Lyman series, if we consider n 1 ​ =1 and n 2 ​ =2,3,…, we can analyze the transition characterizing the second line in the Lyman series when n 1 ​ =1 and n 2 ​ =3.

When we insert these values into the equation, the outcome is as follows:

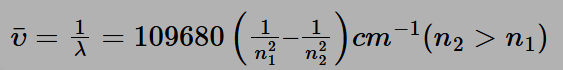
The value of  ν equals 3.28 x 10^4 cm^-1, corresponding to a wavelength ( λ) of 3.05 x 10^-5 cm or 305 nm. This wavelength is situated in the ultraviolet part of the electromagnetic spectrum.

Also Check - Percent by Weight Formula

Example 4: In the Brackett series, given n 1 ​ =4 and n 2 ​ =5,6,…, we

can explore the transition defining the second line in the Brackett series with n 1 ​ =4 and n 2 ​ =6.

Upon substituting these values into the equation, we obtain the following results:

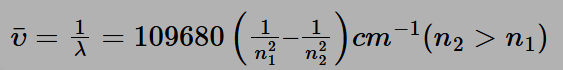
The value of  ν is determined to be 2.42 x 10^3 cm^-1, which corresponds to a wavelength (  λ) of 4.13 x 10^-4 cm or 4130 nm. This wavelength falls within the near-infrared region of the electromagnetic spectrum.