Surface Area of a Hemisphere Formula: Definition, Solved Examples

Surface Area of a Hemisphere Formula: In mathematics, two-dimensional geometry focuses on the x-y plane. The natural progression from this is three-dimensional geometry, which delves into three axes: x, y, and z within the Cartesian plane. Three-dimensional shapes introduce three distinct dimensions - length, breadth, and height.

Three-Dimensional Shapes

Our exploration of three-dimensional shapes often stems from the rotation of their two-dimensional counterparts. A prominent example of this is our planet Earth, which takes on the form of a sphere. A sphere, in turn, derives from the rotation of the two-dimensional circle.

Defining a Hemisphere

A sphere represents a three-dimensional solid where every point on its surface is equidistant from its center. When a plane slices through a sphere, it results in two equal halves known as hemispheres. A sphere can thus be visualized as a combination of two hemispheres.

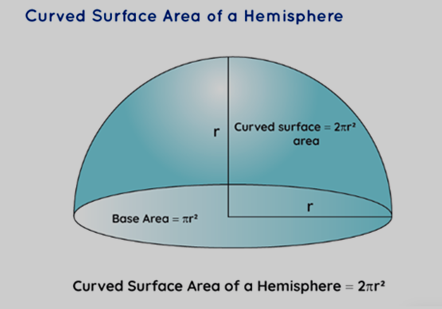
Surface Area of a Hemisphere Formula

Surface area computation for a hemisphere is relatively straightforward due to the circular base of the sphere. Two primary surface area types come into play - the curved surface area and the total surface area.

Curved Surface Area (CSA): This refers to the area covering the outer surface of the hemisphere.

Total Surface Area (TSA): The TSA combines both the curved surface area and the area of the circular base.

The curved surface area of a hemisphere is equivalent to half of the surface area of a complete sphere:

CSA = (1/2) * Surface Area of Sphere

CSA = (1/2) * 4πr²

CSA = 2πr² square units

Calculating Total Surface Area

For the total surface area of the hemisphere, we factor in the base, which is circular. The formula for TSA is as follows:

TSA = Curved Surface Area of Sphere + Base Area of Circle

Given that the base of the hemisphere is circular, we use the formula for the area of a circle:

TSA = 2πr² + πr² = 3πr²

Therefore, the total surface area of a hemisphere equals 3πr² square units. Here, π represents a constant with an approximate value of 3.14, and "r" denotes the radius of the hemisphere.

Surface Area of a Hemisphere Formula Solved Examples

Example 1: Determine the surface area of a hemisphere with a radius of 4 cm.

Solution:

Given:

Radius, r = 4 cm

(i) Curved Surface Area (CSA) of the Hemisphere:

CSA = 2 × 3.14 × 4 × 4

CSA = 3.14 × 32

CSA = 100.48 cm²

(ii) Total Surface Area (TSA) of the Hemisphere:

TSA = 3 × 3.14 × 4 × 4

TSA = 3.14 × 48

TSA = 150.72 cm²

Hence, the hemisphere's curved surface area measures 100.48 cm², while the total surface area is 150.72 cm².

Example 2 : Find the surface area of a hemisphere with a radius of 6.5 cm.

Solution:

Given:

Radius, r = 6.5 cm

(i) Curved Surface Area (CSA) of the Hemisphere:

CSA = (1/2) * Surface Area of Sphere

CSA = (1/2) * 4πr²

CSA = (1/2) * 4 * 3.14 * (6.5 cm)²

CSA = 2 * 3.14 * 42.25 cm²

CSA = 264.74 cm² (rounded to two decimal places)

(ii) Total Surface Area (TSA) of the Hemisphere:

TSA = Curved Surface Area of Sphere + Base Area of Circle

TSA = 2πr² + πr²

TSA = 2 * 3.14 * (6.5 cm)² + 3.14 * (6.5 cm)²

TSA = 2 * 3.14 * 42.25 cm² + 3.14 * 42.25 cm²

TSA = (2 * 3.14 + 3.14) * 42.25 cm²

TSA = 6.28 * 42.25 cm²

TSA = 265.27 cm² (rounded to two decimal places)

Hence, in a hemisphere with a radius of 6.5 cm, the curved surface area is about 264.74 cm², and the total surface area is approximately 265.27 cm².