Area Related To Circles Class 10 Formula

Area Related to Circles class 10 formula concept of circle area refers to the extent of space enclosed by the boundaries of a circle within a two-dimensional plane. Alternatively, it is the spatial occupation within the circumference of a circle. The formula used to compute the area of a circle is A = πr², wherein 'r' signifies the radius of the circle. The standard unit for measuring area is the square unit, such as m², cm², or in².

The formula for circle area proves invaluable for quantifying the expanse covered by circular fields or plots. For instance, if one possesses a circular table, the area formula aids in determining the amount of fabric required to fully cover it. As for the concept of volume in relation to a circle, it does not apply. Being a two-dimensional shape, a circle lacks volume; its attributes are confined to area and perimeter, or circumference.

A deeper exploration of circle area, surface area, and circumference, complemented by illustrative examples, will provide a more comprehensive understanding.

Also Check - Sequence and Series Formula

What is the Area of Circle?

The circle area represents the space encompassed by the limits of a circle's boundary. The expanse enclosed within the circle's perimeter constitutes its area. This measure can be quantified as the aggregate count of square units confined within the circle. The formula for calculating the area of a circle is expressed as A = πr² or πd²/4, denoted in square units. Here,

The constant Pi (π) equals 22/7 or 3.14.

'r' signifies the circle's radius.

'd' signifies the circle's diameter.

Pi (π) serves as the ratio between a circle's circumference and its diameter, an essential mathematical constant with specific properties .

Also Check - Ratio and Proportion Formula

Circle and Parts of a Circle

Before delving into a comprehensive understanding of the circle's area, let's revisit the fundamental components of a circle. A circle is defined as a set of points equidistant from its center, forming a closed geometric entity. Familiar instances of circles in our daily experiences include wheels, pizzas, and circular playing fields.

The magnitude of the expanse or territory confined within the boundaries of a circle is referred to as its area

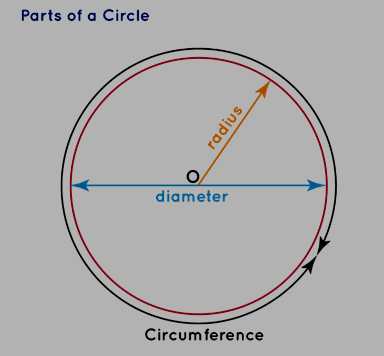
Radius: The measurement from the center to a point on the circle's edge is denoted as the radius of a circle. This pivotal value is typically symbolized by the letter 'r' or 'R'. The radius holds significance in the formulas used for calculating a circle's area and circumference, subjects we will delve into subsequently.

Diameter: When a line passes through the center of a circle and its endpoints touch the circle's boundary, it's referred to as the diameter of the circle. This key dimension is represented by the letter 'd' or 'D'.

Diameter Formula: The diameter of a circle is twice its radius. This relationship is expressed as Diameter = 2 × Radius, equivalently written as d = 2r or D = 2R. If the diameter of a circle is known, the radius can be calculated as: r = d/2 or R = D/2.

Circumference: The circumference of a circle corresponds to the length of its boundary. In other words, a circle's perimeter is synonymous with its circumference. Imagine a rope that perfectly encircles the circle's boundary; its length would precisely match the circle's circumference. The subsequent illustration aids in grasping this concept. The formula for measuring the circumference is:

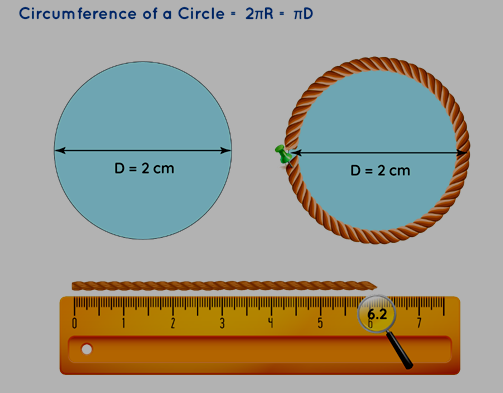
Circumference = πd

where 'r' denotes the circle's radius and π is a mathematical constant approximated as 3.14 or 22/7. For a circle featuring radius 'r' and circumference 'C':

π = Circumference / Diameter

π = C / 2r = C / d

C = 2πr

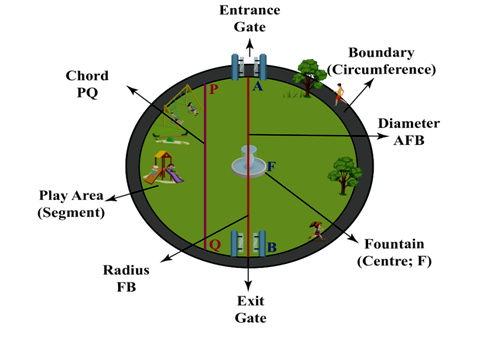
To further clarify these circle attributes, let's turn to a practical example. Envision a circular park, as demonstrated in the illustration below. By referring to the accompanying diagram and table, one can readily identify the distinct components of a circle in a real-world context.

Image of a circular park indicating various circle elements like circumference, radius, diameter, chord, play area, entrance gate, exit gate, and fountain.

Area of Sector

The area of a circular sector represents the region bounded by the sector's perimeter. Each sector emanates from the circle's center. Let's delve into a deeper understanding of the formula for calculating the area of a sector, and explore how this calculation is carried out using both radians and degrees.

Also Check - Data Handling Formula

What is the Area of Sector of a Circle?

The area confined within a circular sector is termed its "sector area." To illustrate, a slice of pizza serves as a tangible example of a sector, representing a portion of the whole. There exist two primary types of sectors: minor and major. A minor sector occupies less space than half of the circle's entirety, whereas a major sector spans more than half.

Download PDF Area Related To Circles Class 10 Formula

The diagram below visually depicts the presence of sectors within a circle. The shaded portion specifically denotes the area of the sector labelled as "OAPB." In this context, the angle ∠ AOB characterizes the sector's angular measure. It's important to recognize that the unshaded region also constitutes a sector within the circle. Consequently, the shaded area pertains to the minor sector, while the unshaded part corresponds to the major sector's area.

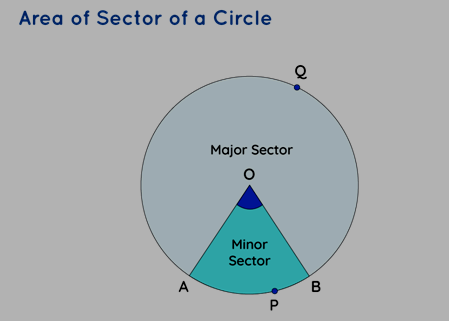
Sector Definition

A circle's sector refers to the segment enclosed by two radii of the circle and the connecting arc between them. It's essentially a distinct portion of a circle marked by these defining elements. The circle itself can be divided into two sectors: the minor sector, which is the smaller portion, and the major sector, encompassing the larger area. One of the most recognizable types of sectors is the semi-circle, constituting exactly half of the circle's entirety.

Also Check - Solid Shapes Formula

Area of Sector Formula

To determine the total space enclosed within a sector, we employ the formula for calculating the sector's area. This area can be computed using the following equations:

• Area of a Sector of a Circle = (θ/360º) × πr², where 'θ' signifies the angle subtended by the arc at the center, measured in degrees, and 'r' represents the circle's radius.
• Area of a Sector of a Circle = 1/2 × r²θ, where 'θ' denotes the angle subtended by the arc at the center, measured in radians, and 'r' stands for the circle's radius.

Also Check - Polynomials Formula

Area of Sector Formula Derivation

We can adopt the unitary method to deduce the formula for a circle sector's area. Recognizing that a complete circle encompasses 360º, the area of a circle with a central angle measuring 360º is represented as πr², with 'r' denoting the circle's radius.For an angle of 1º at the circle's center, the corresponding sector's area equals πr²/360º. Consequently, when the central angle becomes θ, the sector's area can be calculated using the formula: Area of a Sector of Circle = (θ/360º) × πr², where:

θ signifies the angle subtended at the center, specified in degrees.

'r' stands for the circle's radius.

In essence, πr² signifies the entirety of the circle's area, while θ/360º elucidates the proportion of the circle covered by the sector.

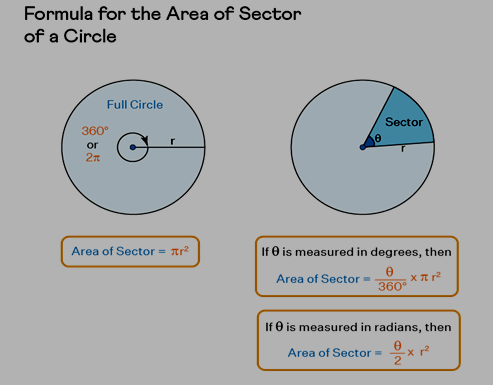
When the central angle is represented by θ in radians, the formula governing the area of a circle's sector becomes: Area of Sector = (1/2) × r²θ, where:

θ stands for the angle subtended at the center, measured in radians.

'r' denotes the circle's radius.

It's important to recognize that semi-circles and quadrants hold a special status within circle sectors. Semi-circles have a central angle of 180°, while quadrants possess a central angle of 90°.

CBSE Class 10 Sample Paper

Segment of a Circle

A circle segment designates the area enclosed between an arc and a chord of the circle. In scenarios where an entity is partitioned into sections, each individual part is termed a segment. Analogously, a circle segment pertains to a distinct portion of the circle. However, it's important to note that a circle segment isn't a random fragment; it's a particular segment that emerges from the intersection of a chord and the circle's boundary arc. In essence, the circle segment encompasses the space framed by a chord (a line that intersects the circle) and an arc (a part of the circle's circumference).

What is the Segment of a Circle?

A circle segment defines the space enclosed between an arc and a chord within the circle. It's important to revisit the definitions of an arc and a chord in the context of a circle:

• An arc represents a specific section of the circle's outer edge or circumference.
• A chord signifies a straight line segment connecting two points on the circle's perimeter.

Two distinct categories of segments exist: minor and major. A minor segment is constituted by a minor arc, while a major segment is formed by a major arc of the circle.

Area of a Segment of Circle

A circle's segment takes shape with the involvement of an arc along with two radii. When combined, these two radii and the chord of the segment constitute a triangular configuration. As a result, the area of a circle segment can be calculated through a process involving the subtraction of the triangle's area from the sector's area. This can be expressed as: Area of Circle Segment = Area of Sector - Area of Triangle.

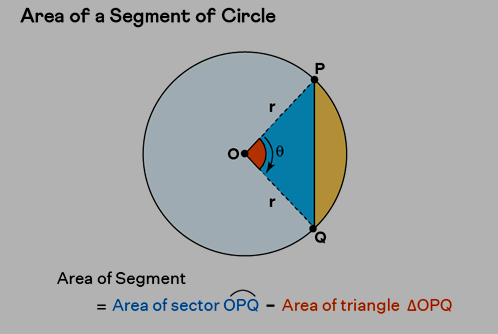
This approach provides a logical foundation for deriving the formulas used to compute the area of a circle segment. It's important to note that this concept applies primarily to minor segments of a circle.

Additionally, if the objective is to determine the area of a major circle segment, one can simply subtract the area of the corresponding minor segment from the overall area of the circle.

Area of a Segment of Circle Formula

Let's consider the minor segment within the circle depicted above, delineated by the chord PQ. The circle has a radius 'r' and is centered at point 'O'. Within this context, each arc of a circle defines a central angle at its center, referred to as the arc's central angle. The angle formed by the arc PQ is denoted as θ. Drawing upon trigonometry principles, we can ascertain that the area of triangle OPQ amounts to (1/2) r² sin θ. Concurrently, the sector OPQ's area can be expressed as:

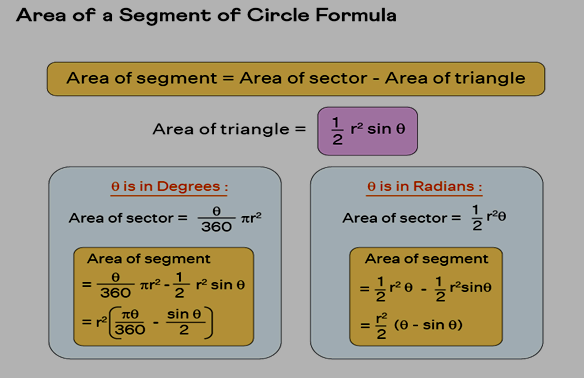
• (θ / 360°) × πr², when 'θ' is in degrees.
• (1/2) × r²θ, when 'θ' is in radians.

With these insights, the area of the minor circle segment is derived as:

• (θ / 360°) × πr² - (1/2) r² sin θ (OR) r² [πθ/360° - sinθ / 2], if 'θ' is in degrees.
• (1/2) × r²θ - (1/2) r² sin θ (OR) (r² / 2) [θ - sin θ], if 'θ' is in radians.

Perimeter of Segment of a Circle

Given a circle segment, it comprises an arc and a chord of the circle. Refer to the same segment as shown in the previous illustration.

The perimeter of this segment can be determined by adding the length of the arc to the length of the chord. This is mathematically expressed as:

Perimeter of Segment = Length of Arc + Length of Chord.

Taking into account the properties of the circle and trigonometric principles, we discern that:

• The length of the arc is 'rθ' if 'θ' is in radians, or πrθ/180 if 'θ' is in degrees.
• The length of the chord equals 2r sin(θ/2).

Hence, the formula for the perimeter of the circle segment is:

• Perimeter of Segment = rθ + 2r sin(θ/2), if 'θ' is in radians.
• Perimeter of Segment = πrθ/180 + 2r sin(θ/2), if 'θ' is in degrees.

Real-Life Example of Area of Sector of Circle

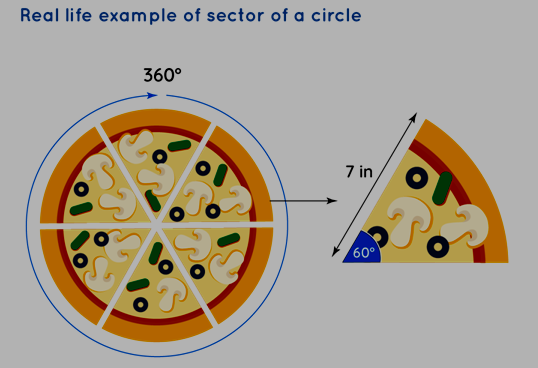
One of the most recognizable instances where the concept of the sector's area comes to life is in the shape of a slice of pizza. The cross-section of a circular pizza remarkably resembles a sector. Consider the illustration below, depicting a pizza neatly divided into six identical slices. Each slice forms a sector, while the radius of the pizza measures 7 inches. Our objective is to determine the sector area for each slice using the sector area formula.

Given that the pizza is partitioned into six equal slices, each slice's central angle amounts to 60°. By plugging this value into the sector area formula, the area of a pizza slice can be calculated as follows:

Area of Pizza Slice = (θ/360°) × πr² = (60°/360°) × (22/7) × 7² = 1/6 × 22 × 7 = 77/3 = 25.67 square units.