X Intercept Formula: Definition, Examples

X Intercept Formula: The x-intercept of a curve signifies the x-coordinate value where the graph intersects the x-axis. In simpler terms, it's the point where the y-coordinate equals zero. Understanding the x-intercept is crucial in graph analysis.

X Intercept Formula

Several formulas are associated with intercepts, derived by setting y = 0 in equations and solving for x. Here are some key formulas:

General Form of a Line: ax + by + c = 0

x-intercept = -c/a

Slope-Intercept Form: y = mx + c

x-intercept = -c/m

Point-Slope Form: y - b = m(x - a)

x-intercept = (am - b)/m

Intercept Form: x/a + y/b = 1

x-intercept = (a, 0)

Finding X Intercept on a Graph

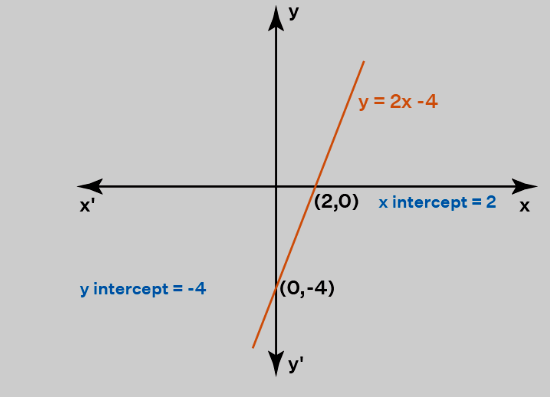
To find the x-intercept of a line represented by y = mx + b, simply substitute y = 0 into the equation and solve for x. For instance, if you have the equation y = 2x - 4:

Example:

0 = 2x - 4

4 = 2x

2 = x

So, the x-intercept of y = 2x - 4 is 2.

Finding Equation of a Line Using X Intercept

Let's say you're given a slope (m) and an x-intercept (-5) and need to find the equation of a line. Follow these steps:

Use the x-intercept formula: x = -c/m

Substitute the values: -5 = -c/2

Solve for c: c = 10

Now, plug the values of c and m into the equation y = mx + c:

Equation of the line: y = 2x + 10

X Intercept Examples

Example 1:

Given 2y = 3x - 6, calculate the x-intercept and y-intercept.

Solution:

x-intercept: 2x = 3x - 6 => 2x = 6 => x = 3

y-intercept: 2y = -6 => y = -3

So, the line has an x-intercept of 3 and a y-intercept of -3.

Example 2:

A line with slope -2 passes through point P(a, 1). If the sum of both intercepts equals 6, find the value of a.

Solution:

General equation: y - 1 = -2(x - a)

x-intercept = 1/2 + a

y-intercept = 1 + 2a

Sum of intercepts: 1/2 + a + 1 + 2a = 3a + 5/2

Set this equal to 6 and solve for a:

3a + 5/2 = 6

3a = 11/2

a = 3/2

So, the value of a is 3/2.

Example 3:

Calculate the x-intercept of the parabola y = x^2 - 3x + 2.

Solution:

Set y = 0 in the equation:

0 = x^2 - 3x + 2

Solve for x:

x = 2 and x = 1

The parabola intersects the x-axis at x = 2 and x = 1.

Example 4:

Determine the x-intercepts of the equation 3x + 2y = 6.

Solution:

Rearrange the equation: 2y = -3x + 6

Divide by 2: y = (-3/2)x + 3

To find the x-intercept, set y = 0 and solve for x:

0 = (-3/2)x + 3

(-3/2)x = -3

x = (-3)/(-3/2) = 2

So, the x-intercept of 3x + 2y = 6 is 2.

Example 5:

Given the equation of a circle as (x - 4)^2 + y^2 = 16, find the x-intercepts.

Solution:

Set y = 0 in the equation:

(x - 4)^2 + 0 = 16

Simplify and solve for x:

(x - 4)^2 = 16

x - 4 = ±√16

x - 4 = ±4

x = 4 ± 4

So, the x-intercepts are x = 8 and x = 0.

Example 6:

Find the x-intercepts of the quadratic function f(x) = 2x^2 - 5x - 3.

Solution:

To find the x-intercepts of the quadratic equation 2x^2 - 5x - 3 = 0, we can use the quadratic formula:

x = (-(-5) ± √((-5)^2 - 4(2)(-3))) / (2(2))

Simplifying further:

x = (5 ± √(25 + 24)) / 4

x = (5 ± √49) / 4

x = (5 ± 7) / 4

Therefore, the x-intercepts of the function f(x) = 2x^2 - 5x - 3 are x = 3/2 and x = -1.

Example 7:

For the exponential function y = 2^x, find the x-intercept.

Solution:

Set y = 0:

2^x = 0

However, 2^x is always positive for any real value of x, so it does not have an x-intercept in the real number system.

In this case, there is no real x-intercept for the exponential function y = 2^x because exponential functions never equal zero for real values of x.

These additional examples showcase how to find x-intercepts in various types of equations and functions, including linear, quadratic, and exponential forms.