CBSE Worksheet for chapter-7 Lines and Angles class 9

Worksheet For class 9

Find CBSE Worksheet for chapter-7 Lines and Angles class 9

CLASS-9

BOARD: CBSE

Mathematic Worksheet - 7

TOPIC: Lines and Angles

This page is prepared by the Academic team of Physics Wallah which consists of CBSE Board Worksheet for Class 9 Maths. Students of Class 9 Maths can get a free Worksheet for Class 9 Maths in PDF format prepared as per the newest syllabus and examination pattern in your schools.

Before solving the Worksheet for Class 9 one must read the textbook of your school board exam and try to read the notes given in Physics Wallah Class 9 notes sections. Students can also download free pdf of Class 9 Maths Notes prepared by teachers and solve important problems provided here with solutions on daily basis to get more scores in school exams and tests. Physics Wallah worksheets for Class 9 CBSE can help students practice with tests and quickly revise lessons learned in the classroom with essential resources such as video lessons, short notes, and sample papers.

Class 9 Board is one of the most important year for every student and need a good planning and right study material to score good marks in your final exam. For other CBSE Worksheets for class 9 Mathematics check out the main page of Physics Wallah.

Summary

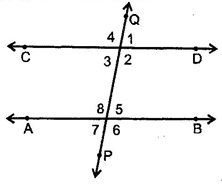
1. Transversal: A line which intersects two or more given parallel lines at distinct points is called a transversal of the given lines.
2. Corresponding angles: 1 & 5, 4 & 8, 2 & 6, 3 & 7 are pairs of corresponding angles.
3. Alternate interior angles: 3 & 5, 2 & 8 are the pairs of alternate interior angles.
4. Consecutive interior angles: 2 & 5, 3 & 8, are pairs of consecutive interior angles.
5. Vertically opposite angles: in figure, 1 = 3, 2 = 4, 5 = 7 & 6 = 8.

Objective- 1

Q1. Two parallel lines have

1. a common point
2. two common points
3. no common point
4. infinite common points

Q2. An angle is 14^o more than its complementary angle then angle is

1. 38^o
2. 52^o
3. 50^o
4. None of these

Q3. X lies in the interior of BAC. If ∠BAC=70^oand ∠BAX=42^o , ∠CAX=

1. 28⁰
2. 29⁰
3. 27⁰
4. 30⁰

Q4. Two angles whose measure are a and b are such that 2a-3b=60⁰ then =?, if they form a linear pair

1. 0
2. 8/5
3. 1/2
4. 2/3

Q5. Which one of the following is correct?

1. If two parallel lines are intersected by a transversal, then alternate angles are equal.
2. If two parallel lines are intersected by a transversal, then sum of the interior angles on the same side of transversal is 180^o
3. If two parallel lines are intersected by a transversal, then corresponding angles are equal
4. All of these.

Objective- 2

Q1. Two supplementary angles are in ratio 4 : 5, then the angles are:

1. 80°, 100°
2. 70°, 110°
3. 80°, 120°
4. None

Q2. If an angle differs from its complement by 10°, find the larger angle.

1. 45°
2. 50°
3. 95°
4. 60°

Q3. In the given figure, OP and OQ bisect BOC and AOC respectively, then POQ is.

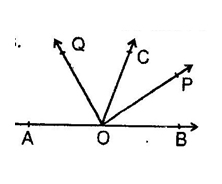
1. 90°
2. 45°
3. 135°
4. 180°

Q4. In the given fig if l II m, n II p and 1 = 85° then 2 is

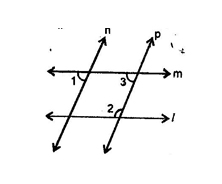
1. 95°
2. 110°
3. 135°
4. 85°

Q5. An larger angle is 14° more than its complementary angle then angle is:

1. 38°
2. 52°
3. 50°
4. none of these

Q6. X lies in interior of ∠BAC. If ∠BAC = 70° and ∠BAX = 42° then ∠XAC = ?

1. 28°
2. 29°
3. 27°
4. 30°

Q7. If the supplement of an angle is three times its complement, then angle is:

1. 40°
2. 35°
3. 50°
4. 45°

Q8. Two angles whose measures are a & b are such that 2a – 3b = 60°, if they form a linear pair then find .

1. 0
2. 8/5
3. 1/2
4. 2/3

Q9. The supplement of an angle is one third of itself. Then the angle is:

1. 135°
2. 45°
3. 140°
4. None

Q10. In given figure, if ∠BOC = 7x + 20° and ∠COA = 3x, then the value of x for which AOB becomes a straight line.

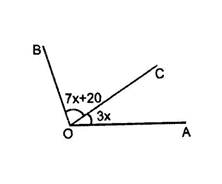
1. 15°
2. 12°
3. 16°
4. None

Q11. In given figure if AB II DF, AD II FG ∠BAC = 65°, ∠ACB=55^o ∠FGH is:

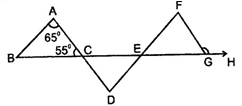
1. 120°
2. 125°
3. 115°
4. 140°

Q12. In given figure, AB II ED and ∠ABC = 30°, ∠EDC = 70° then x is:

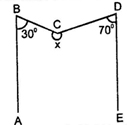
1. 240°
2. 125°
3. 260°
4. None

Q13. In the given figure, if EC II AB, ∠ECD = 70° and ∠BDO = 20°, then ∠OBD is-

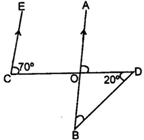
1. 20°
2. 50°
3. 60°
4. 70°

Q14. Given AB II CD, x° =

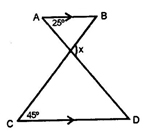
1. 20°
2. 70°
3. 110°
4. 35°

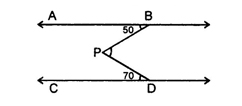
Q15. As shown in the figure . If point P is between these two lines such that m∠ABP = 50° and m∠CDP = 70° then find ∠BPD.

1. 120°
2. 70°
3. 110°
4. 50°

Q16. The measure of that angle which is four times its supplement is:

1. 36
2. 144°
3. 155°
4. 180°

Solutions

Objective-1

1. 3
2. 2
3. 1
4. 2
5. 4

Objective-2

1. 1
2. 2
3. 1
4. 1
5. 2
6. 1
7. 4
8. 2
9. 1
10. 3
11. 2
12. 3
13. 2
14. 2
15. 1
16. 2