
NCERT Solutions for Class 8 Maths chapter - 14 Factorisation
The NCERT solutions for class 8 maths chapter 14 Factorisation is prepared by academic team of Physics Wallah. We have prepared solutions for all exercise of chapter 14. Given below is step by step solutions of all questions given in NCERT textbook for chapter 14. Read chapter 14 theory make sure you have gone through the theory part of chapter 14 from NCERT textbook and you have learned the formula of the given chapter. Physics Wallah prepared a detail notes and additional questions for class 8 maths with short notes of all maths formula of class 8 maths. Do read these contents before moving to solve the exercise of NCERT chapter 14. This NCERT solution contains questions, answers, pictures and explanations for the complete Chapter 14 taught in Class 8.
NCERT Solutions for Class 8 Maths Exercise 14.1
Question 1.
Find the common factors of the given terms.
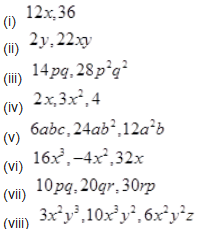
Solution :
(i) 12x = 2 × 2 × 3
36 = 2 × 2 × 3 × 3
Hence, the common factors are 2, 2 and 3 = 2 × 2 × 3 = 12
(ii) 2y = 2 ×y
22xy = 2 × 11 × x × y
Hence the common factors are
2 and y = 2 × y = 2y
(iii) 14 pq = 2×7× p × q
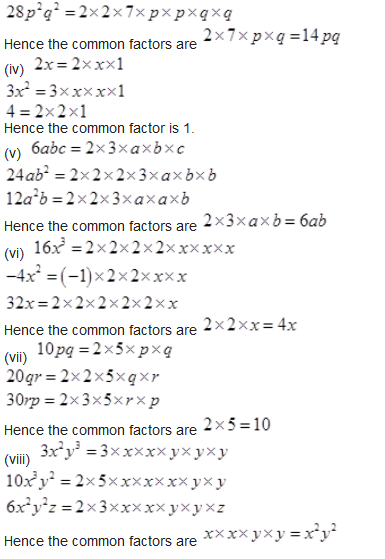
Question 2.
Factorize the following expressions.
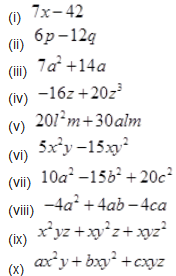
Solution :

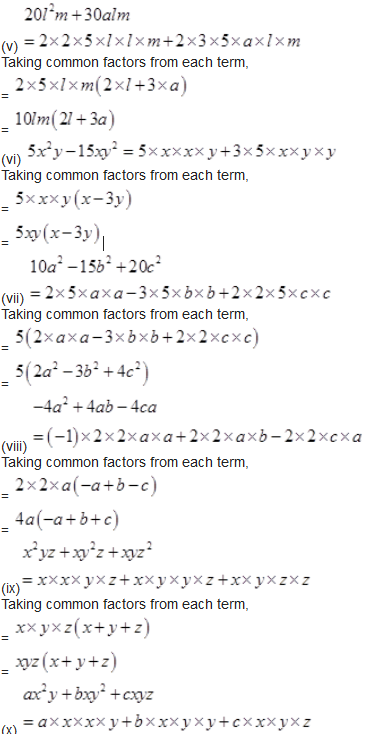
Taking common factors from each term,
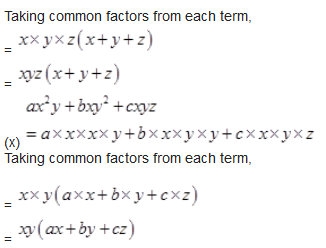
Question 3.
Factorize:
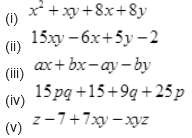
Solution :
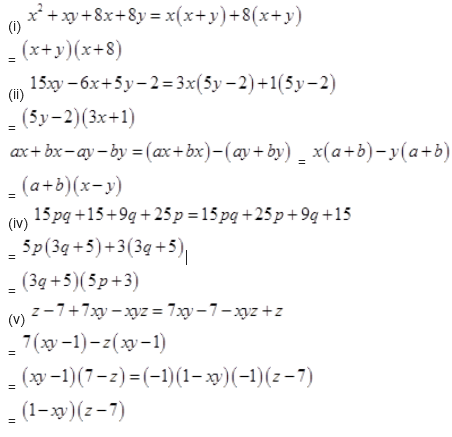
NCERT Solutions for Class 8 Maths Exercise 14.2
Question 1.
Factorize the following expressions:
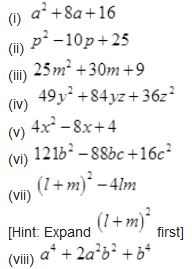
Solution :
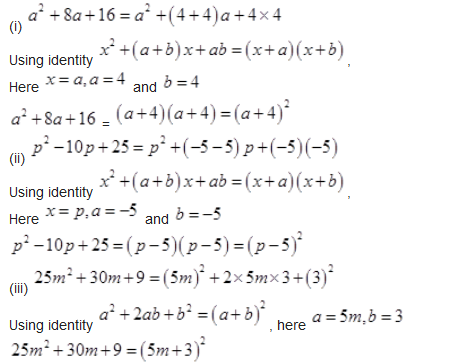
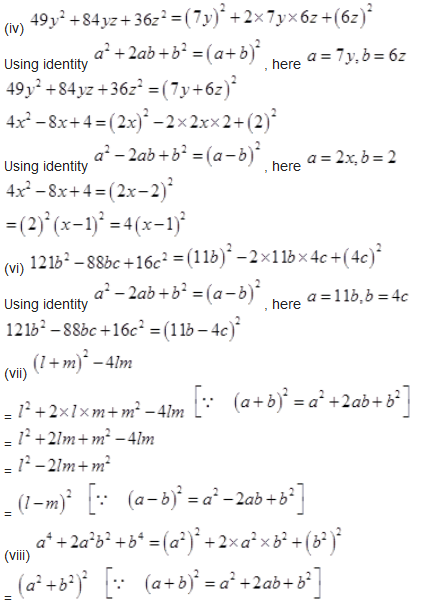
Question 2.
Factorize
(i)
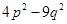
(ii)
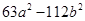
(iii)
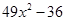
(iv)
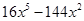
(v)
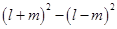
(vi)
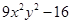
(vii)
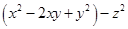
(viii)
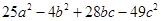
Solution :
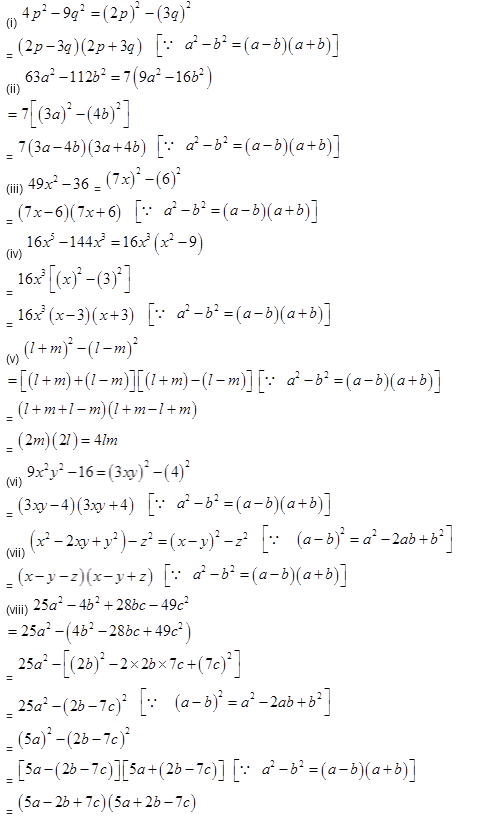
Question 3.
Factorize the expressions:
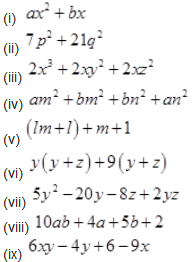
Solution :
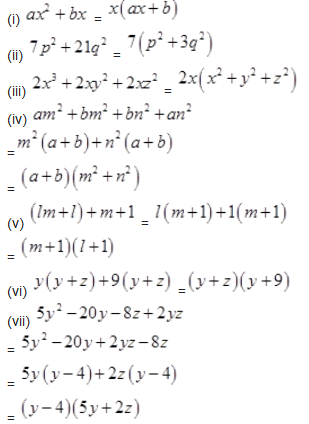
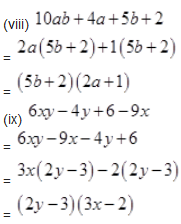
Question 4.
Factorize:
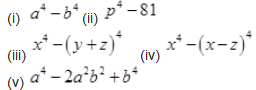
Solution :
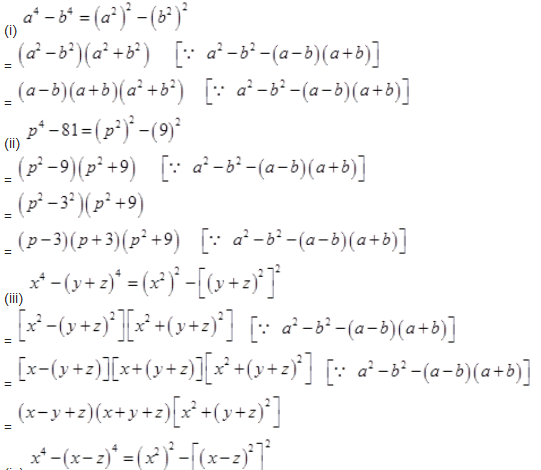
(iv)
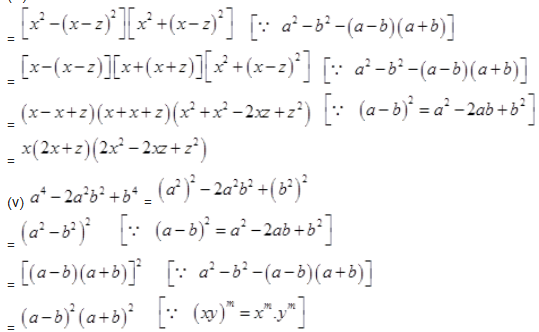
Question 5.
Factorize the following expressions:
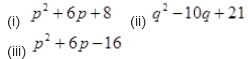
Solution :
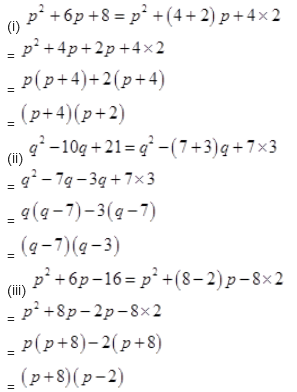
NCERT Solutions for Class 8 Maths Exercise 14.3
Question 1.
Carry out the following divisions:
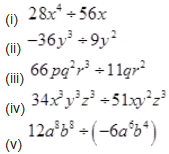
Solution :
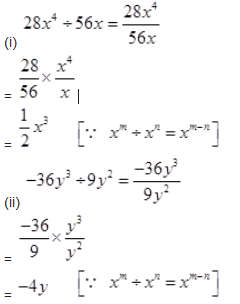
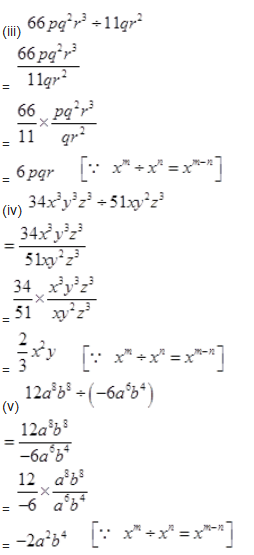
Question 2.
Divide the given polynomial by the given monomial:
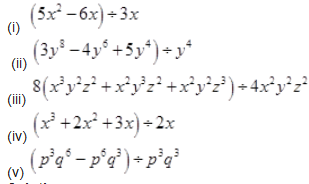
Solution :
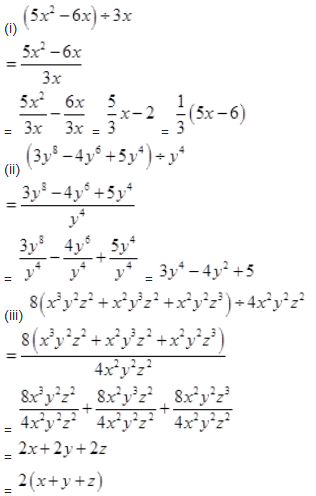
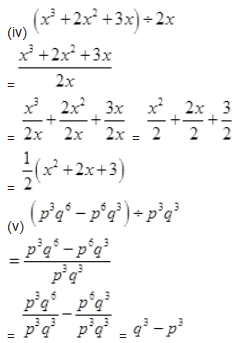
Question 3.
Work out the following divisions:
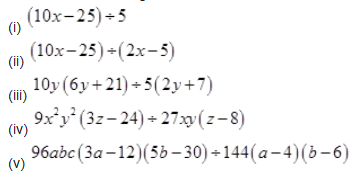
Solution :
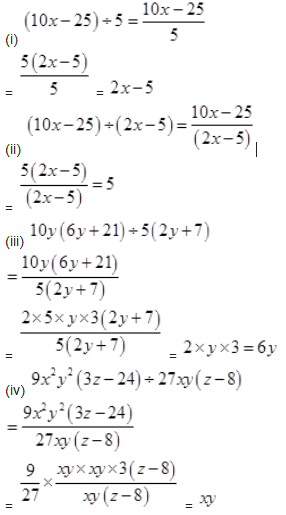
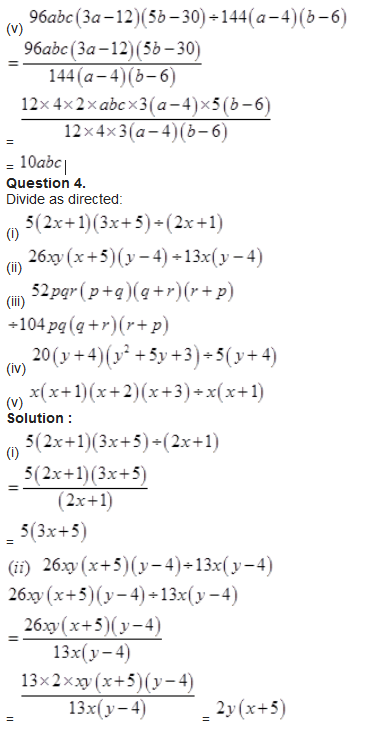
(iii)
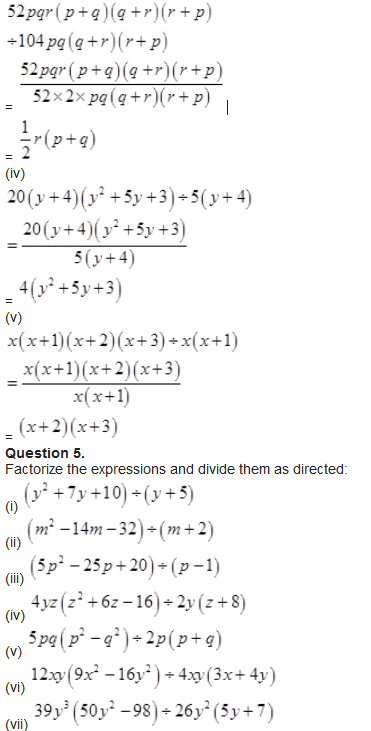
Solution :
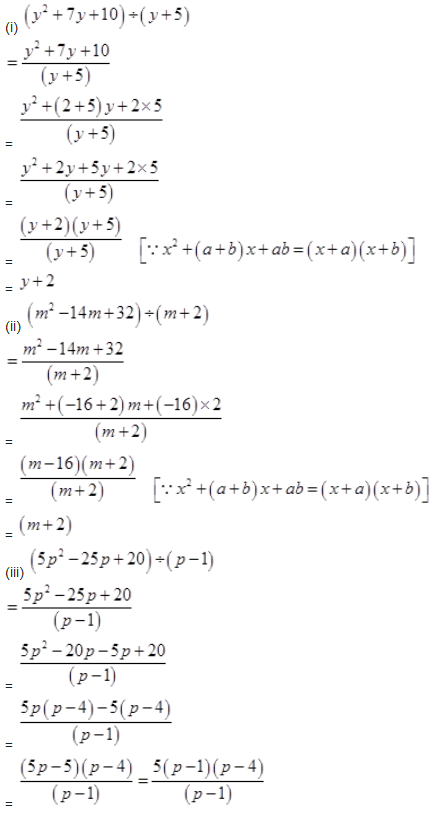
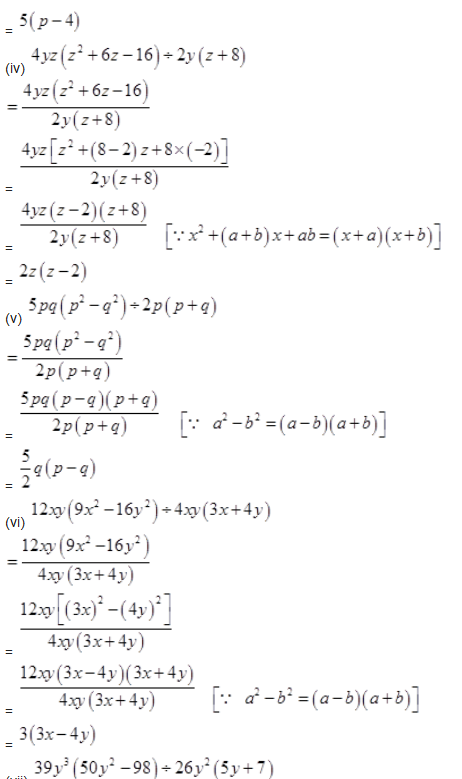
![]()


Solution :


Question 13.

Solution :

Solution :
L.H.S. =
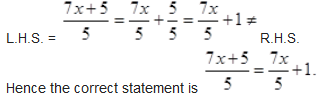 R.H.S.
R.H.S.
Notes,worksheet and solved question for Maths class 8
- class 8 maths notes on chapter Liner equation in one variable
- class 8 maths notes on chapter algebric expression
- class 8 maths notes on chapter Mensuration
- class 8 maths notes on chapter Square and square roots
- class 8 maths notes on chapter statistice
- class 8 maths notes on chapter practical Geometry
- class 8 maths notes on chapter commericial maths
- class 8 maths notes on chapter solid shape
- class 8 maths notes on chapter quadrilaterals
- class 8 maths notes on chapter exponents
- class 8 maths notes on chapter factorisation
- class 8 maths notes on chapter inverse proporation
- class 8 maths notes on chapter cube and cube roots
Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below
chapter wise online test for class 8 maths









