
NCERT Solutions for Class 8 Maths chapter-9 Algebraic Expressions and Identities
NCERT solutions for class 8 maths chapter 9 Algebraic Expressions and Identities is prepared by academic team of Physics Wallah. We have prepared solutions for all exercise with importants questions of chapter 9. Given below is step by step solutions of all questions given in NCERT textbook for chapter-9. Read chapter 9 theory make sure you have gone through the theory part of chapter-9 from NCERT textbook and you have learned the formula of the given chapter. Physics Wallah prepared a detail notes and additional questions for class 8 maths with short notes of all maths formula of class 8 maths. do read these contents before moving to solve the exercise of NCERT chapter 9.
NCERT Solutions for Class 8 Maths Exercise 9.1
Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i)
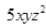
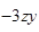
(ii) 1 + x + x²
(iii)
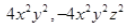
(iv) 3 - pq + qr -rp
(v)
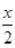 +
+
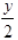 - xy
- xy
(vi) 3 - pq + qr -rp
Solution :
(i) Terms:
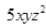 and
and
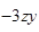
Coefficient in
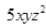 is 5 and in
is 5 and in
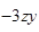 is
-3
is
-3
(ii) Terms: 1, x and x²
Coefficient of
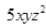 and coefficient of
x²
is 1.
and coefficient of
x²
is 1.
(iii) Terms:
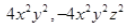 and
z²
and
z²
Coefficient in
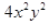 is 4, coefficient of
is 4, coefficient of
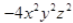 is -4 and coefficient of
z²
is 1.
is -4 and coefficient of
z²
is 1.
(iv) Terms: 3, -pq, qr and -rp
Coefficient of
-pq
is
-1,
coefficient of
qr
is 1 and coefficient of
-rp
is
![]()
(v) Terms:
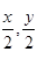 and
-xy
and
-xy
Coefficient of
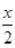 is
is
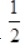 coefficient of
coefficient of
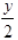 is
is
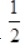 and coefficient of
-xy
is
-1.
and coefficient of
-xy
is
-1.
(vi) Terms: 0.3a, -0.6ab and 0.5b
Coefficient of 0.3a is 0.3, coefficient of -0.6ab is -0.6 and coefficient of 0.5b is 0.5.
Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories:
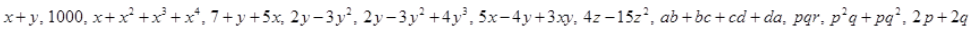
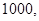
Solution :
(i) Since
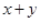 contains two terms. Therefore it is binomial.
contains two terms. Therefore it is binomial.
(ii) Since 1000 contains one terms. Therefore it is monomial.
(iii) Since
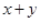 contains four terms. Therefore it is a polynomial and it does not fit in above three categories.
contains four terms. Therefore it is a polynomial and it does not fit in above three categories.
(iv) Since
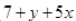 contains three terms. Therefore it is trinomial.
contains three terms. Therefore it is trinomial.
(v) Since
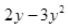 contains two terms. Therefore it is binomial.
contains two terms. Therefore it is binomial.
(vi) Since
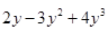 contains three terms. Therefore it is trinomial.
contains three terms. Therefore it is trinomial.
(vii) Since
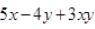 contains three terms. Therefore it is trinomial.
contains three terms. Therefore it is trinomial.
(viii) Since
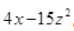 contains two terms. Therefore it is binomial.
contains two terms. Therefore it is binomial.
(ix) Since
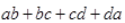 contains four terms. Therefore it is a polynomial and it does not fit in above three categories.
contains four terms. Therefore it is a polynomial and it does not fit in above three categories.
(x) Since pqr contains one terms. Therefore it is monomial.
(xi) Since
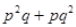 contains two terms. Therefore it is binomial.
contains two terms. Therefore it is binomial.
(xii) Since 2p + 2q contains two terms. Therefore it is binomial.
Question 3.
Add the following:
(i)
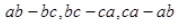
(ii)
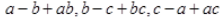
(iii)
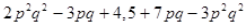
(iv)
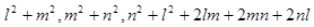
Solution :
(i)
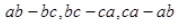
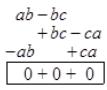
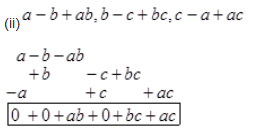
Hence the sum if 0.
Hence the sum is ab + ac + bc.

Question 4.
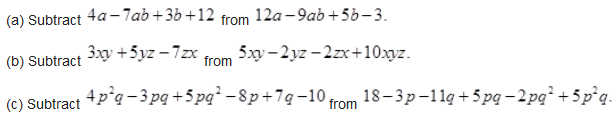
Solution :
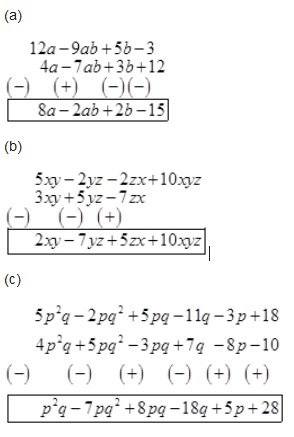
NCERT Solutions for Class 8 Maths Exercise 9.2
Question 1.
Find the product of the following pairs of monomials:
(i)
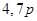
(ii)
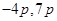
(iii)
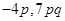
(iv)
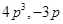
(iv) 4p ,0
Solution :
(i)
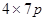 =
=
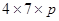 =
=
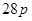
(ii)
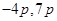 =
=
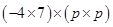
=
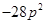
(iii)
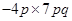 =
=
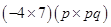
=
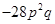
(iv)
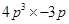 =
=
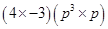
=
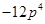
(v)
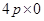 =
=
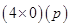 = 0
= 0
Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively:
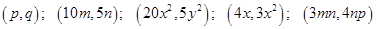
Solution :
(i) Area of rectangle
=
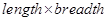
=
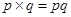 sq. units
sq. units
(ii) Area of rectangle
=
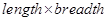
=
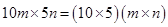
= 50mn sq. units
(iii) Area of rectangle =
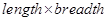
=
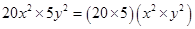
=
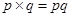 sq. units
sq. units
(iv) Area of rectangle =
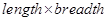
=
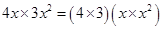
=
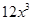 sq. units
sq. units
(v) Area of rectangle =
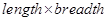
=
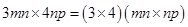
=
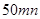 sq. units
sq. units
Question 3.
Complete the table of products:
(i)

Solution :
(i)
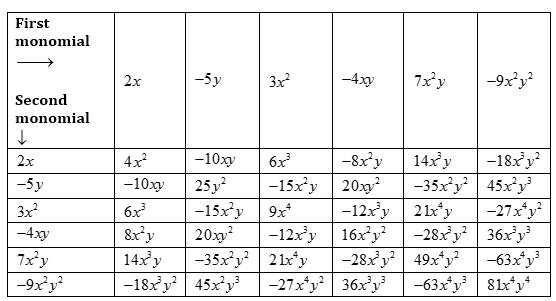
Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively:
(i)
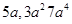
(ii)
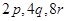
(iii)
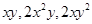
(iv)
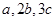
Solution :
(i) Volume of rectangular box
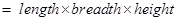
=
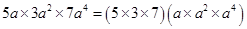
=
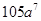 cubic units
cubic units
(ii) Volume of rectangular box
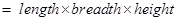
=
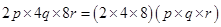
=
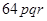 cubic units
cubic units
(iii) Volume of rectangular box
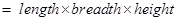
=
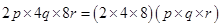
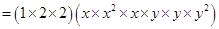
=
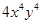 cubic units
cubic units
(iv) Volume of rectangular box
=
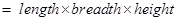
=
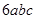 cubic units
cubic units
Question 5.
Obtain the product of:
(i)
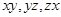
(ii)
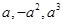
(iii)
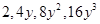
(iv)
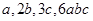
(v)
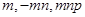
Solution :
(i)
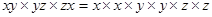
=
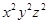
(ii)
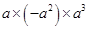 =
=
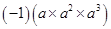
=
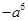
(iii)
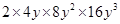
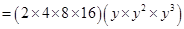
=
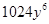
(iv)
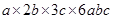
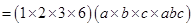
=
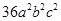
(v)
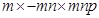
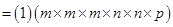
=
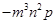
NCERT Solutions for Class 8 Maths Exercise 9.3
Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i)
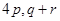
(ii)
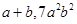
(iii)
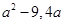
(iv)
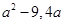
(v)
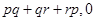
Solution :
(i)
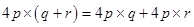
=
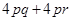
(ii)
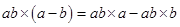
=
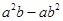
(iii)
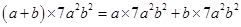
=
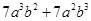
(iv)
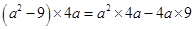
=
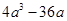
(v)
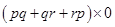 =
=
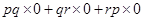
= 0 + 0 + 0 = 0
Question 2.
Complete the table:
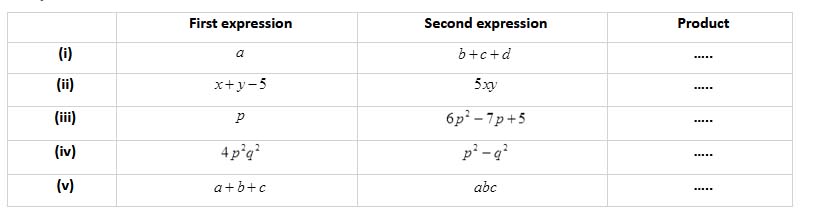
Solution :


Question 3.
Find the product:
(i)
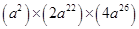
(ii)
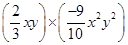
(iii)
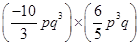
(iv)
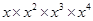
Solution :
(i)
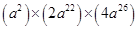
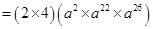
=
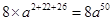
(ii)
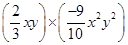
=
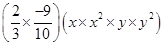
=
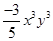
(iii)
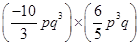
=
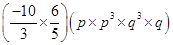
=
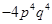
(iv)
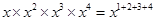 =
=
![]()
Question 4.
(a) Simplify:
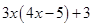 and find values for
and find values for
(i)
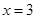
(ii)
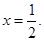
(b) Simplify:
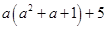 find its value for
find its value for
(i)
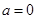
(ii)
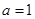
(iii)
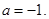
Solution :
(a)
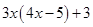
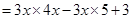
=
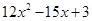
(i) For
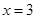
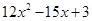
=
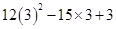
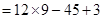 = 108 – 45 + 3 = 66
= 108 – 45 + 3 = 66
(ii) For
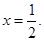
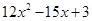
=
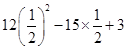
=
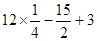
=
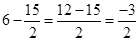
(b)
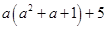
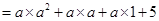
=
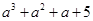
(i) For a= 0,
![]()
=
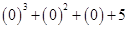
= 0 + 0 + 0 + 5 = 5
(ii) For a = 1
![]()
=
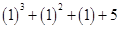
= 1 + 1 + 1 + 5 = 8
(iii) For
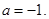
![]()
=
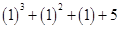
=
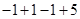 =
=
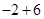 =4
=4
Question 5.
(a) Add:
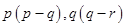 and
and
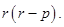
(b) Add:
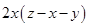 and
and
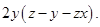
(c) Subtract:
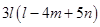 from
from
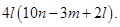
(d) Subtract:
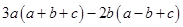 from
from
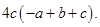
Solution :
(a)
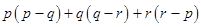
=
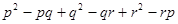
=
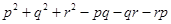
(b)
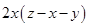 +
+
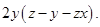
=
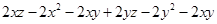
=
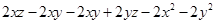
=
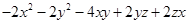
(c)
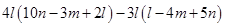
=
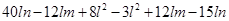
=
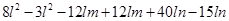
=
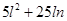
(d)
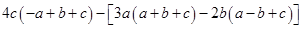
=
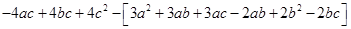
=
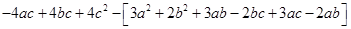
=
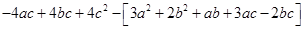
=
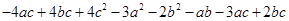
=
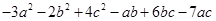
=
![]()
NCERT Solutions for Class 8 Maths Exercise 9.4
Question 1.
Multiply the binomials:
(i)
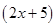 and
and
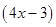
(ii)
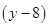 and
and
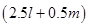
(iii)
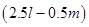 and
and
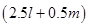
(iv)
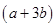 and
and
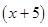
(v)
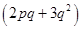 and
and
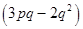
(vi)
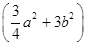 and
and
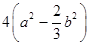
Solution :
(i)
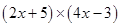
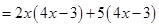
=
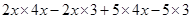
=
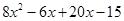
=
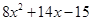
(ii)
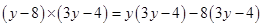
=
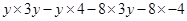
=
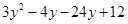
=
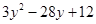
(iii)
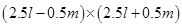
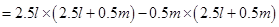
=
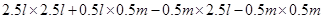
=
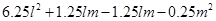
=
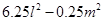
(iv)
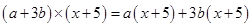
=
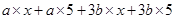
=
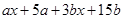
(v)
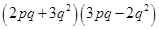
=
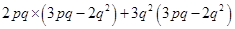
=
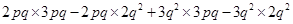
=
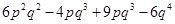
=
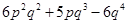
(vi)
![]()
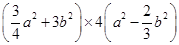
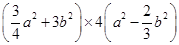
=
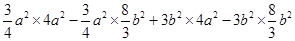
=
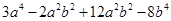
=
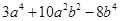
Question 2.
Find the product:
(i)
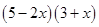
(ii)
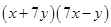
(iii)
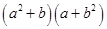
(iv)
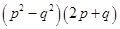
Solution :
(i)
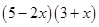
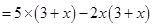
=
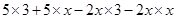
=
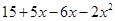 = 15 - x -2x²
= 15 - x -2x²
(ii)
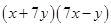
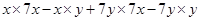
=
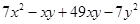
=
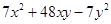
(iii)
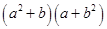
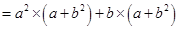
=
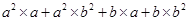
=
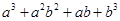
(iv)
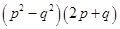
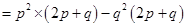
=
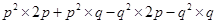
=
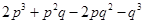
Question 3.
Simplify:
(i)
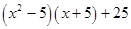
(ii)
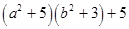
(iii)
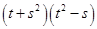
(iv)
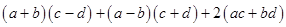
(v)
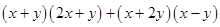
(vi)
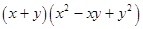
(vii)
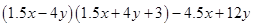
(viii)
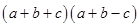
Solution :
(i)
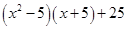
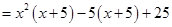
=
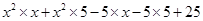
=
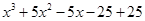
=
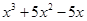
(ii)
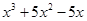
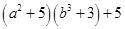
=
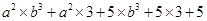
=
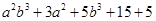
=
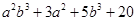
(iii)
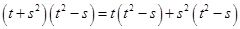
=
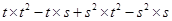
=
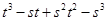
(iv)
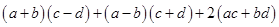
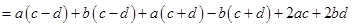
=
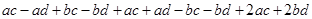
=
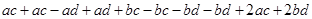
=
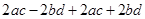
= 4ac
(v)
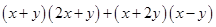
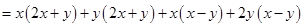
=
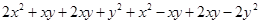
=
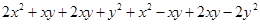
=
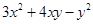
(vi)
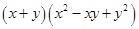
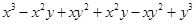
=
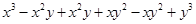
=
![]()
(vii)
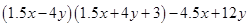
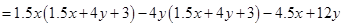
=
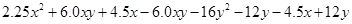
=
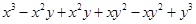
=
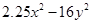
(viii)
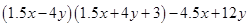
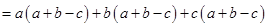
=
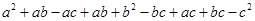
=
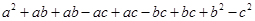
=
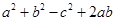
Notes,worksheet and solved question for Maths class 8
- class 8 maths notes on chapter Liner equation in one variable
- class 8 maths notes on chapter algebric expression
- class 8 maths notes on chapter Mensuration
- class 8 maths notes on chapter Square and square roots
- class 8 maths notes on chapter statistice
- class 8 maths notes on chapter practical Geometry
- class 8 maths notes on chapter commericial maths
- class 8 maths notes on chapter solid shape
- class 8 maths notes on chapter quadrilaterals
- class 8 maths notes on chapter exponents
- class 8 maths notes on chapter factorisation
- class 8 maths notes on chapter inverse proporation
- class 8 maths notes on chapter cube and cube roots
Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below
chapter wise online test for class 8 maths









