
CBSE Class 9 Maths Notes Chapter 12: We are offering a free PDF of the CBSE Class 9 Maths Chapter 12 Herons Formula notes to assist students study the chapter efficiently and do well on the test. This will enable students to answer questions based on Heron's formula quickly and accurately during exams.
Experts have created these CBSE Class 9 Maths Herons Formula notes, making sure to utilize straightforward language that facilitates rapid and easy topic comprehension for students. Before tests, students may easily review all of the key terms from each chapter with the aid of these notes, which are an excellent reference resource. Students in class 9 can use the link below to get the Herons Formula revision notes for Maths Chapter 12.CBSE Class 9 Maths Notes Chapter 12 Overview
Notes for Heron's Formula Class 9 Students need this material to help them navigate the fascinating world of geometry: CBSE Maths Chapter 12. These carefully written notes—which are freely downloadable as PDF files—deconstruct the mysterious Heron's Formula and enable students to compute triangle areas quickly and accurately. They offer a thorough grasp of this mathematical instrument, covering everything from its creation to real-world uses. These notes provide students with a skill set for problem-solving that goes beyond the classroom; they are not merely for exam preparation. They are an essential tool for students who want to do well in their CBSE Class 9 maths curriculum because of their instructional worth and accessibility.CBSE Class 9 Maths Notes Chapter 12 PDF
Here we have provided CBSE Class 9 Maths Notes Chapter 12 pdf for the students so that they can prepare easily for their exams by referring to these notes. Students can use these notes at any time without the internet by downloading them. Students can use these notes before the exams to clear their concepts better.CBSE Class 9 Maths Notes Chapter 12 PDF
CBSE Class 9 Maths Notes Chapter 12
Area of Triangle

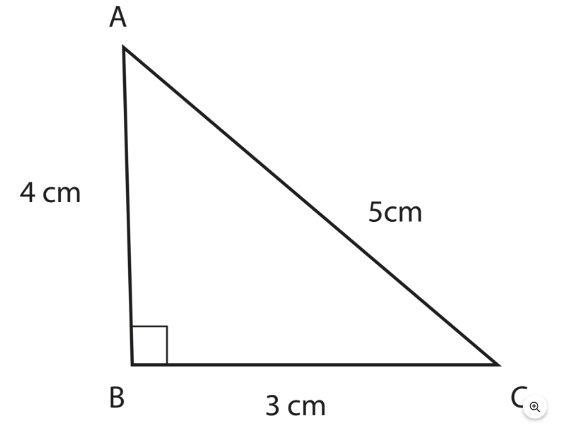
 The area of an isosceles triangle, an equilateral triangle, and a right-angle triangle may all be calculated using this formula.
However, we apply Heron's formula to get the area of the triangle when it is difficult to determine the triangle's height, like in the case of the scalene triangle.
The area of an isosceles triangle, an equilateral triangle, and a right-angle triangle may all be calculated using this formula.
However, we apply Heron's formula to get the area of the triangle when it is difficult to determine the triangle's height, like in the case of the scalene triangle.
Types of Triangles
Based on sides – a) Equilateral b) Isosceles c) Scalene Based on angles – a) Acute-angled triangle b) Right-angled triangle c) Obtuse-angled triangle
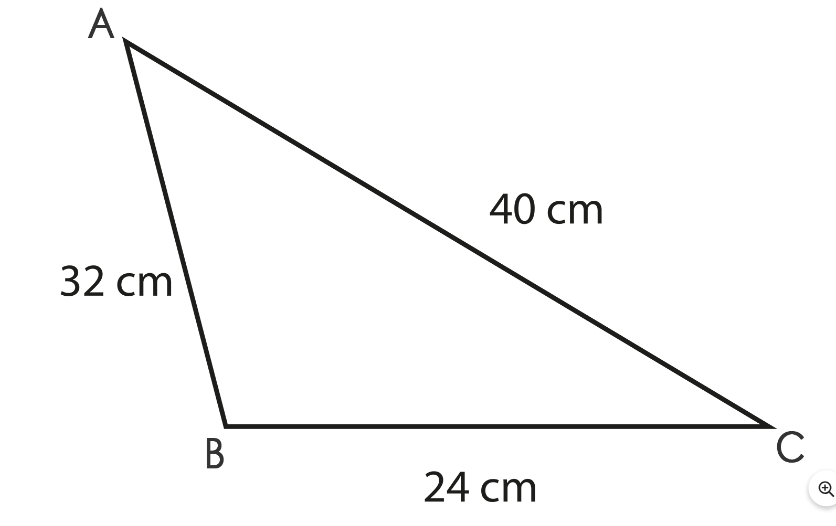
Area of Triangle – by Heron’s Formula:


Area of Quadrilateral using Heron’s Formula:
By connecting one of a quadrilateral's diagonals, it is possible to divide it into two triangular sections. Next, we can calculate the area of two triangular portions using Heron's Formula. We may then calculate the quadrilateral's area by adding them. As an illustration, let a rhombus ABCD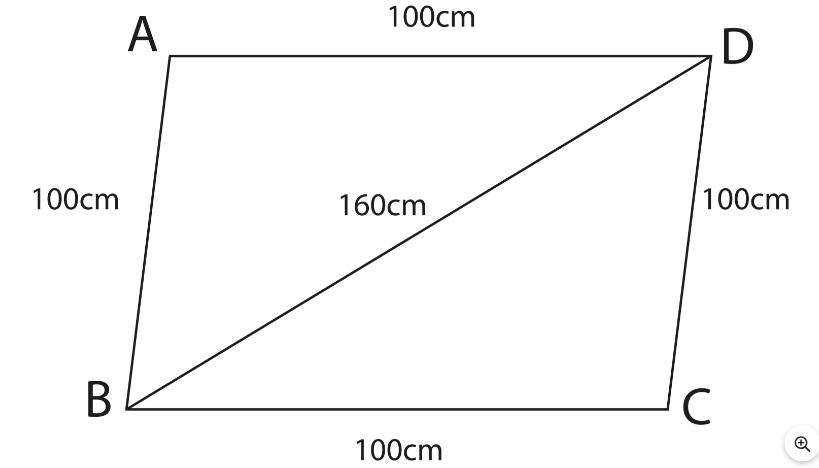


How to Calculate the Area of Triangle Using Herons Formula?
Heron's formula is a key reference in this field. If we have the lengths of all three sides of the triangle, we can use this formula to determine the area of the triangle. The two steps shown below can be used to calculate this:Step 1: Calculate the “s” (half of the triangle’s perimeter):
S= a+ b = c2
Step 2: Then calculate the Area.
This formula is credited to Hero (or Heron) of Alexandria, a Greek Engineer, and Mathematician in 10 – 70 Anno Domini (AD).
Benefits of CBSE Class 9 Maths Notes Chapter 12
If you wish to swiftly gain a deeper understanding of every subject covered in Maths Chapter 12, consult these notes. Your editing process will be strengthened by the remarks' simple writing style. Students who desire concise study materials to review their topics can use the Class 9 Maths Chapter 12 revision notes. Our carefully prepared Class 9 Maths Chapter 12 notes are factually accurate and provide a precise explanation of every chapter concept. Students who like to study in the comfort of their own homes with the highest caliber materials at no cost typically opt for the Class 9 Maths Chapter 12 revision notes free PDF download option.CBSE Class 9 Maths Notes Chapter 12 FAQs
Which is the hardest chapter in maths class 9?
What is the main point of herons formula class 9?
Which is the most scoring chapter in class 9 maths?










