CBSE Class 9 Maths Notes Chapter 4:
In CBSE Class 9 Maths Notes Chapter 4, we explore Linear Equations in Two Variables. These notes help us understand basic concepts related to equations involving two variables and how they can be represented on graphs as straight lines.
We learn about different forms of linear equations, such as standard form (ax + by = c), slope-intercept form (y = mx + c), and point-slope form (y - yβ = m(x - xβ)). The notes also teach us methods to solve these equations, like substitution and elimination
By studying these notes, we can easily grasp the concepts of linear equations and apply them to solve problems in various scenarios.
CBSE Class 9 Maths Notes Chapter 4 PDF
You can access the CBSE Class 9 Maths Notes Chapter 4 Linear Equations in Two Variables PDF through the provided link.Β Understanding how to solve these equations algebraically and graphically is crucial for solving various real-world problems.
The PDF contains detailed explanations, solved examples, and practice problems to help you grasp the concepts effectively. It is a valuable resource to enhance your understanding of linear equations and excel in your mathematics studies.
CBSE Class 9 Maths Notes Chapter 4 PDF
CBSE Class 9 Maths Notes Chapter 4 Linear Equations in Two Variables
Linear equation in one variable
A linear equation in one variable is an algebraic equation that involves only one variable raised to the power of 1 and constants. It can be represented in the form
ππ₯+π=0
a
x
+
b
=
0
, where
π
a
and
π
b
are constants, and
π₯
x
is the variable. The solutions to a linear equation in one variable represent the values of the variable that make the equation true.
These solutions can be found by various methods such as algebraic manipulation, graphing, or using properties of equality. Linear equations in one variable are fundamental in algebra and are widely used in various fields of mathematics and real-world applications.
Linear Equation in 2 Variables
A linear equation in two variables is an algebraic equation involving two variables, typically denoted as
π₯
x
and
π¦
y
, where both variables have a degree of one.
The general form of a linear equation in two variables is
ππ₯+ππ¦+π=0
a
x
+
b
y
+
c
=
0
, where
π
a
,
π
b
, and
π
c
are constants, and
π
a
and
π
b
cannot both be zero. This equation represents a straight line when plotted on a Cartesian plane, where each point on the line satisfies the equation.
Solution of Linear Equation
A linear equation has a unique solution when there exist only one point which satisfies the linear equation.
For example: Solution of
2
x
+
6
=
2
2π₯+6=2
is
2
x
+
6
=
2
2π₯+6=2
2
x
=
2
β
6
2π₯=2β6
2
x
=
β
4
2π₯=β4
x
=
β
4
2
π₯=β42
x
=
β
2
π₯=β2
In
2
x
+
6
=
2
2π₯+6=2
has only one variable
x
π₯
therefore
x
π₯
has unique solution.Β Also, geometrically it will be a point on rectangular axes whose ordinate will be
0
0
-
A system of linear equation has unique solution when the system of lines intersects each other at only one point.
-
A linear equation in two variables have infinitely many solutions means there are more than one ordered pair which satisfy the equation.
-
For example: Solution of
2
x
+
3
y
=
12
2π₯+3π¦=12
are
The following value
(
3
,
2
)
,
(
0
,
4
)
,
(
6
,
0
)
(3,2),(0,4),(6,0)
of
x
π₯
and
y
π¦
satisfies the equation
2
x
+
3
y
=
12
2π₯+3π¦=12
therefore they are the solutions of
2
x
+
3
y
=
12
2π₯+3π¦=12
.
-
A system of linear equation has infinitely many solution if the system of lines coincides each other which means each point on the system of line will be the solution.
-
For example: System of linear equations
β
6
x
+
4
y
=
2
β6π₯+4π¦=2
and
3
x
β
2
y
=
β
1
3π₯β2π¦=β1
have infinitely many solution because these two lines coincide each other as shown in graph below
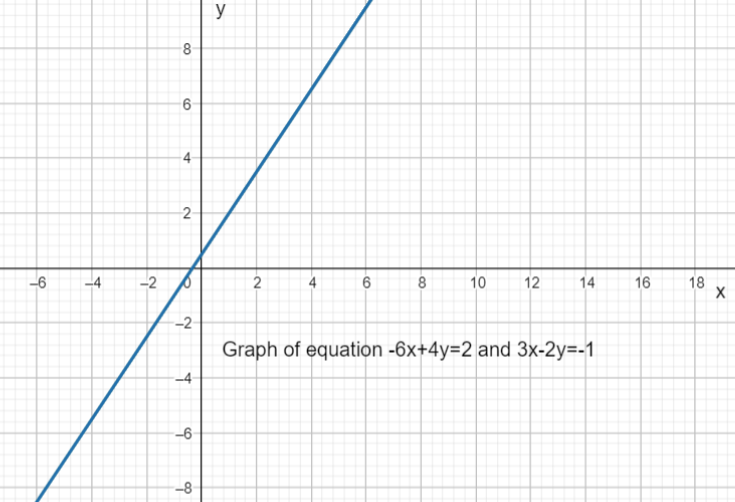
Graph of Linear Equation in Two Variables:
We know that linear equation in two variables can have infinitely many solutions and we get every solution in form of pair of values.
So, we can plot these values on coordinate plane and draw the graph of linear equation in two variables.
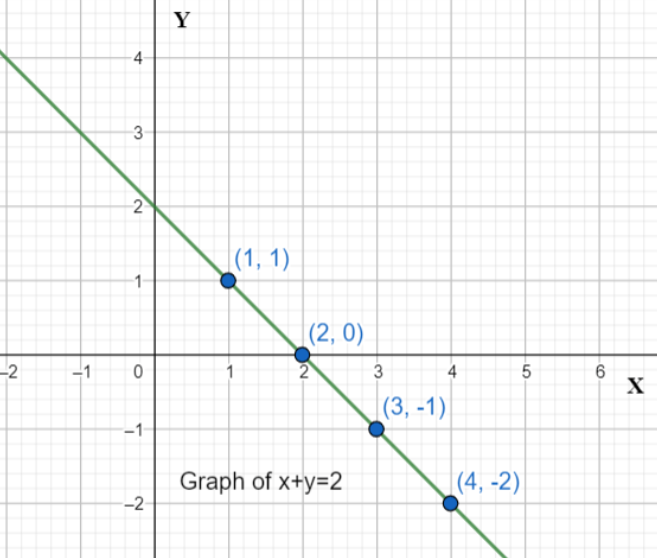
For e.g. β Let us draw the graph for the equationΒ x+y=2π₯+π¦=2
Let us draw a table for the values of xπ₯Β and yπ¦
Now, Plotting the values of
x
π₯
and
y
π¦
in the coordinate plane
Equations of Line Parallel to X-axis and Y-axis:
-
Linear equation in two variables is written as
a
x
+
b
y
+
c
=
0
ππ₯+ππ¦+π=0
if we put
y
=
0
π¦=0
, the equation becomes
a
x
+
c
=
0
ππ₯+π=0
. The Graph of equation
a
x
+
c
=
0
ππ₯+π=0
is a straight line parallel to the y-axis.
-
On the other hand, if we put
x
=
0
π₯=0
in
a
x
+
b
y
+
c
=
0
ππ₯+ππ¦+π=0
, the equation becomes
b
y
+
c
=
0
ππ¦+π=0
.The Graph of equation
b
y
+
c
=
0
ππ¦+π=0
is a straight line parallel to the x-axis.
-
Equation of x-axis is
y
=
0
π¦=0
because at x-axis y-coordinates are always zero and the coordinate form of any point on x-axis will be
(
x
,
0
)
(π₯,0)
-
Equation of y-axis is
x
=
0
π₯=0
because at y-axis x-coordinates are always zero and the coordinate form of any point on y-axis will be
(
0
,
y
)
(0,π¦)
-
Graph below represents the equation of x-axis and y-axis
-
If in a coordinate point
(
x
,
y
)
(π₯,π¦)
value of
x
π₯
is a positive constant then the point will lie on the right side of y-axis and if it is a negative constant then the point will lie on the left side of y-axis.
-
Similarly, if the value of
y
π¦
is a positive constant then the point will lie on the upper side of x-axis and if it is negative constant then the point will lie on the lower side of x-axis.
Benefits of CBSE Class 9 Maths Notes Chapter 4 Linear Equations in Two Variables
-
Concept Clarity:
These notes provide clear explanations of concepts related to linear equations in two variables, helping students understand the topic better.
-
Comprehensive Coverage:
The notes cover all the important topics and subtopics of the chapter, ensuring that students do not miss any crucial information.
-
Structured Format:
The notes are organized in a structured manner, making it easier for students to follow and review the content.
-
Useful Examples:
They include solved examples that illustrate the application of concepts in different scenarios, aiding in better comprehension.
-
Practice Questions:
The notes contain practice questions at the end of each topic, allowing students to test their understanding and proficiency.
-
Exam Preparation:
By using these notes, students can effectively prepare for their exams, as they cover the entire syllabus comprehensively.
