CBSE Class 9 Maths Notes Chapter 5: In CBSE Class 9 Maths Chapter 5, we learn about Euclid's Geometry. Euclid was a famous mathematician from ancient Greece who laid down the basic rules for geometry in his book "Elements."
This chapter helps us understand the basic ideas of geometry, like points, lines, and angles. We also learn about Euclid's five main rules, which are like the building blocks of geometry. With these rules, we can make different shapes, such as lines, triangles, and circles, using a straightedge and compass. By studying this chapter, we become better at understanding shapes and solving problems related to them. It's like learning the fundamental rules of a game before playing it.CBSE Class 9 Maths Notes Chapter 5 PDF
The PDF linked below has easy-to-understand notes for CBSE Class 9 Maths Chapter 5, "Introduction to Euclid's Geometry." These notes cover Euclid's fundamental concepts, like points, lines, planes, angles, and geometric figures' construction using basic tools. By studying these notes, students can grasp the core principles of Euclidean geometry and how they're applied in solving mathematical problems.CBSE Class 9 Maths Notes Chapter 5 PDF
CBSE Class 9 Maths Notes Chapter 5 Introduction to Euclids Geometry
Introduction to Euclid Geometry
- Geometry's origin lies in addressing practical needs of ancient civilizations.
- It was used to demarcate land boundaries, determine granary volumes, and construct structures like the Egyptian pyramids.
- Even during the Vedic period, geometry was utilized for constructing altars.
- The term "geometry" originates from the Greek words "geo" (earth) and "metrein" (to measure).
- Around 300 BC, Euclid organized geometry into a systematic framework with his work "Elements."
- Euclid's approach, known as the Euclidean method, relied on a small set of self-evident assumptions.
- These assumptions, termed axioms and postulates, were used to derive numerous other propositions systematically.
- "Elements" served as a textbook in Western Europe for centuries, outlining definitions, postulates, and common notions.
- Euclid's work laid the foundation for plane and solid geometry.
Euclid's Definitions
- A point is defined as something that has no part.
- A line is described as a length without breadth.
- The ends of a line are points.
- A straight line is one that lies evenly with all the points on itself.
- A surface is characterized as having only length and breadth.
- The edges of a surface are lines.
- A plane surface is one that lies evenly with straight lines on itself.
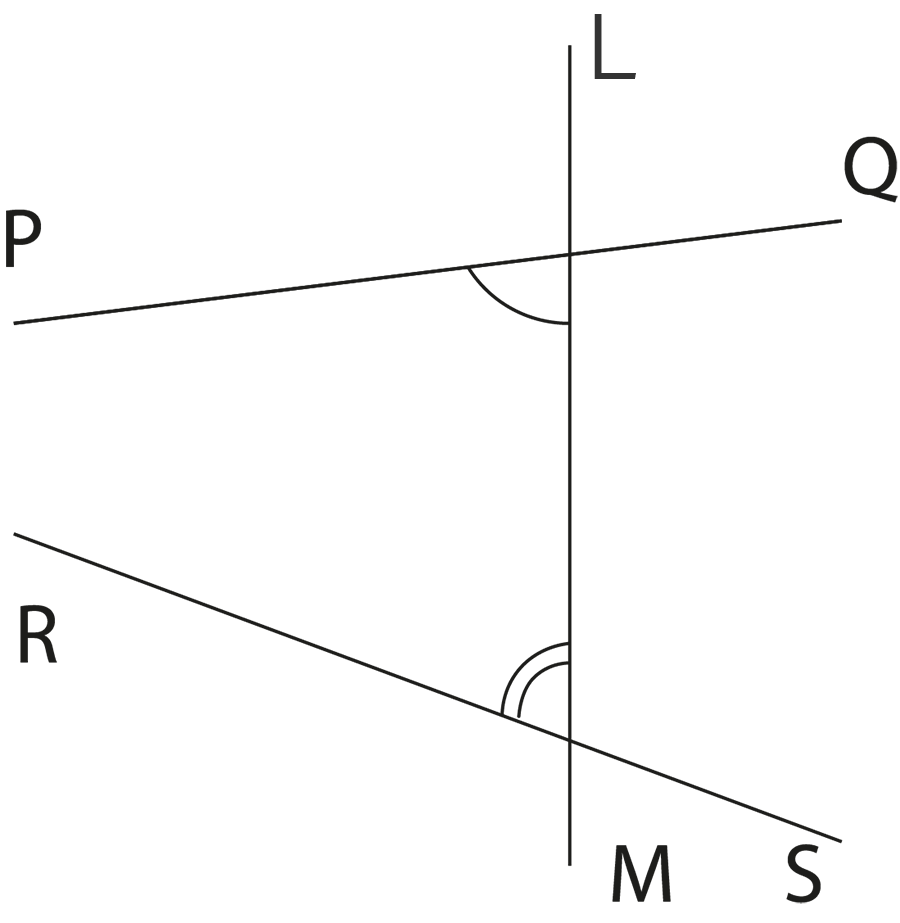
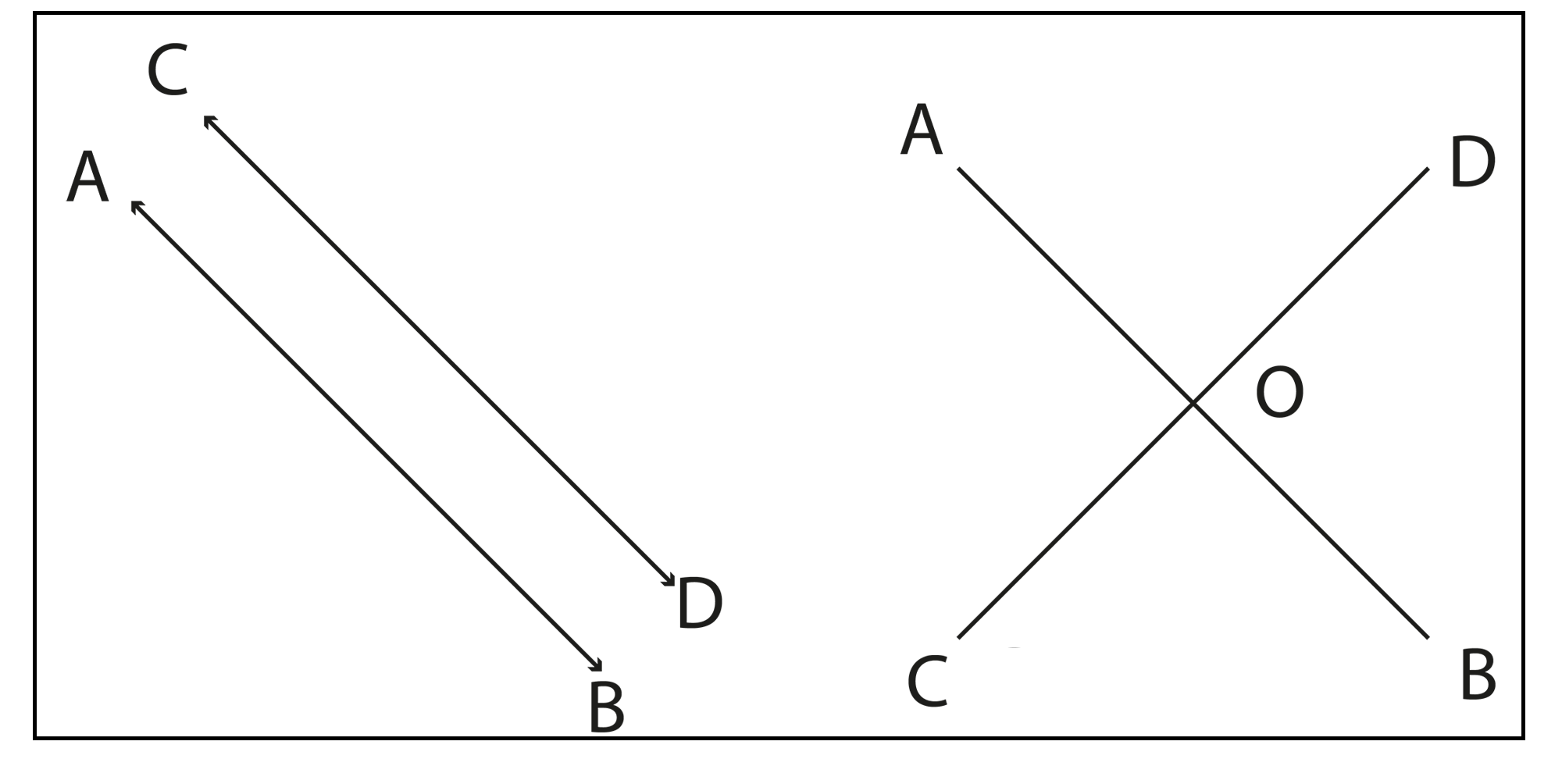
Euclid's Axioms
CBSE Class 9 Maths Notes Chapter 5 FAQs
What is Euclid's Geometry?
Euclid's Geometry refers to the principles, postulates, and theorems formulated by the ancient Greek mathematician Euclid in his seminal work "Elements." It laid the foundation for the study of geometry and served as the standard textbook for geometry for over 2,000 years.
Why is Euclid's work significant in the history of mathematics?
Euclid's "Elements" is considered one of the most influential works in the history of mathematics. It organized the existing knowledge of geometry into a systematic and logical framework, providing a rigorous approach to mathematical reasoning. Euclid's axioms and postulates laid the groundwork for deductive reasoning and influenced the development of mathematics for centuries.
How can students benefit from studying Euclid's Geometry?
Studying Euclid's Geometry helps students develop critical thinking skills, logical reasoning abilities, and problem-solving techniques. It provides a solid foundation in geometric principles and cultivates an appreciation for the beauty and elegance of mathematical proofs.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App