NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 (Limits and Derivatives)
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 contains all the questions with detailed solutions. Students are advised to solve these questions for better understanding of the concepts in exercise 13.3.
Krati Saraswat9 Sept, 2025
Share
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 Limits and Derivatives is prepared by the academic team of Physics Wallah. We have prepared NCERT Solutions for all exercises of Chapter 13. Below is step by step solutions to all questions given in the NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 Limits and Derivatives.
NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 (Limits and Derivatives) Overview
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 cover several important topics. It is highly recommended for students to review each topic thoroughly in order to gain a comprehensive understanding of the concepts taught in the chapter and make optimal use of the provided solutions. These solutions are the result of dedicated efforts by the Physics Wallah teachers aimed at assisting students in grasping the concepts covered in this chapter. By going through and practicing these solutions, the objective is for students to achieve excellent results in their exams effortlessly.NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3
Solve The Following Questions of NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3:
Question 1. An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red? Solution : The urn contains 5 red and 5 black balls. Let a red ball be drawn in the first attempt. ∴ P (drawing a red ball) = 5/10 = 1/2 If two red balls are added to the urn, then the urn contains 7 red and 5 black balls. P (drawing a red ball) = 7/12 Let a black ball be drawn in the first attempt. ∴ P (drawing a black ball in the first attempt) = 5/10 = 1/2 If two black balls are added to the urn, then the urn contains 5 red and 7 black balls. P (drawing a red ball) = 5/12 Therefore, probability of drawing second ball as red is
Let A be the event of getting a red ball. 
The probability of drawing a ball from the first bag, given that it is red, is given by P (E 2 |A). By using Bayes’ theorem, we obtain 
Question 3. Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostler? 
The probability that a randomly chosen student is a hostler, given that he has an A grade, is given by P(E 1 |A). By using Bayes’ theorem, we obtain 
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.1
Question 4. In answering a question on a multiple choice test a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1/4 be the probability that he guesses. Assuming that a student who guesses the answer, will be correct with probability 1/4. What is the probability that a student knows the answer given that he answered it correctly?Solution : Let E 1 and E 2 be the respective events that the student knows the answer and he guesses the answer. Let A be the event that the answer is correct.
The probability that the student answered correctly, given that he knows the answer, is 1. ∴ P (A|E 1 ) = 1 Probability that the student answered correctly, given that he guessed, is 1/4. 
The probability that the student knows the answer, given that he answered it correctly, is given by P(E 1 |A). By using Bayes’ theorem, we obtain 
NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.5
Question 5. A laboratory blood test is 99% effective in detecting a certain disease when it is, in fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e., if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?Solution : Let E 1 = The person selected is suffering from certain disease, E 2 = The person selected is not suffering from certain disease and A = The doctor diagnoses correctly Since E 1 and E 2 are events complimentary to each other, ∴ P (E 1 ) + P (E 2 ) = 1 ⇒ P (E 2 ) = 1 − P (E 1 ) = 1 − 0.001 = 0.999 Let A be the event that the blood test result is positive.
Probability that a person has a disease, given that his test result is positive, is given by P (E 1 |A). By using Bayes’ theorem, we obtain 
Question 6. There are three coins. One is a two headed coin, another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows head, what is the probability that it was the two headed coin? Solution : Let E 1 = a two headed coin, E 2 = a biased coin, E 3 = an unbiased coin and A = A head is shown
Let A be the event that the coin shows heads. A two-headed coin will always show heads. 
Probability of heads coming up, given that it is a biased coin= 75% 
Since the third coin is unbiased, the probability that it shows heads is always 1/2.. 
The probability that the coin is two-headed, given that it shows heads, is given by P (E 1 |A). By using Bayes’ theorem, we obtain 
Question 7. An insurance company insured 2000 scooter driver, 4000 car drivers and 6000 truck drivers. The probability of accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver? 
The probability that the driver is a scooter driver, given that he met with an accident, is given by P (E 1 |A). By using Bayes’ theorem, we obtain 
Question 8. A factory has two machines A and B. Past record shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B? Solution : Let E 1 and E 2 be the respective events of items produced by machines A and B. Let X be the event that the produced item was found to be defective. ∴ Probability of items produced by machine A, P (E 1 ) = 60% = 3/5 Probability of items produced by machine B, P (E 2 ) = 40% = 2/5 Probability that machine A produced defective items, P (X|E 1 ) = 2% = 2/100 Probability that machine B produced defective items, P (X|E 2 ) = 1% = 1/100 The probability that the randomly selected item was from machine B, given that it is defective, is given by P (E 2 |X). By using Bayes’ theorem, we obtain 
Question 9. Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability if 0.3, if the second group wins. Find the probability that the new product introduced was by the second group.
Solution : Let E 1 and E 2 be the respective events that the first group and the second group win the competition. Let A be the event of introducing a new product. P (E 1 ) = Probability that the first group wins the competition = 0.6 P (E 2 ) = Probability that the second group wins the competition = 0.4 P (A|E 1 ) = Probability of introducing a new product if the first group wins = 0.7 P (A|E 2 ) = Probability of introducing a new product if the second group wins = 0.3 The probability that the new product is introduced by the second group is given by P (E 2 |A). By using Bayes’ theorem, we obtain
Question 10. Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4 she tosses a coin once and noted whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 and 4 with the die? Solution : Let E 1 be the event that the outcome on the die is 5 or 6 and E 2 be the event that the outcome on the die is 1, 2, 3, or 4. 
Let A be the event of getting exactly one head. P (A|E 1 ) = Probability of getting exactly one head by tossing the coin three times if she gets 5 or 6 = 3/8 P (A|E 2 ) = Probability of getting exactly one head in a single throw of coin if she gets 1, 2, 3, or 4 = 1/2 The probability that the girl threw 1, 2, 3, or 4 with the die, if she obtained exactly one head, is given by P (E 2 |A). By using Bayes’ theorem, we obtain 
Question 11. A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job for 30% of the time and C on the job for 20% of the time. A defective item is produced, what is the probability that it was produced by A? Solution : Let E 1 = the item is manufactured by the operator A, E 2 = the item is manufactured by the operator B, E 3 = the item is manufactured by the operator C and A = the item is defective 
Let X be the event of producing defective items. 
The probability that the defective item was produced by A is given by P (E 1 |A). By using Bayes’ theorem, we obtain 
Question 12. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond. Solution : Let E1 = the missing card is a diamond, E 2 = the missing card is a spade, E 3 = the missing card is a club, E 4 = the missing card is a heart and A = drawing of two heart cards from the remaining cards. Let E 1 and E 2 be the respective events of choosing a diamond card and a card which is not diamond. Let A denote the lost card. Out of 52 cards, 13 cards are diamond and 39 cards are not diamond.
When one diamond card is lost, there are 12 diamond cards out of 51 cards. Two cards can be drawn out of 12 diamond cards in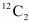 
ways. Similarly, 2 diamond cards can be drawn out of 51 cards in 
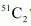ways. The probability of getting two cards, when one diamond card is lost, is given by P (A|E 1 ). 
When the lost card is not a diamond, there are 13 diamond cards out of 51 cards. Two cards can be drawn out of 13 diamond cards in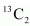 
ways whereas 2 cards can be drawn out of 51 cards in 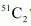ways. The probability of getting two cards, when one card is lost which is not diamond, is given by P (A|E 2 ). 
The probability that the lost card is diamond is given by P (E 1 |A). By using Bayes’ theorem, we obtain 
= 11/2/25 = 11/50 Question 13. Probability that A speaks truth is 4/5 A coin is tossed. A report that a head appears. The probability that actually there was head is: (A) 4/5 (B) 1/2 (C) 1/5 (D) 2/5 Solution : Let A be the event that the man reports that head occurs in tossing a coin and let E 1 be the event that head occurs and E 2 be the event head does not occur. E 1 : A speaks truth E 2 : A speaks false Let X be the event that a head appears. P(E1)=45 Therefore, P(E2)=1-P(E1)=1-45=15 If a coin is tossed, then it may result in either head (H) or tail (T). The probability of getting a head is 1/2 whether A speaks truth or not.
The probability that there is actually a head is given by P (E 1 | X) 
Hence, option (A) is correct. Question 14. If A and B are two events such that A ⊂ B and P (B) ≠ 0, then which of the following is correct: 
Solution : If A ⊂ B, then A ∩ B = A ⇒ P (A ∩ B) = P (A) Also, P (A) < P (B) 
Hence, option (C) is correct.
NCERT Solutions For Class 12 Maths Chapter 13 Exercise 13.3 FAQs
How can NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 help in exam preparation?
These solutions provide step-by-step explanations and solutions to problems, helping students understand the concepts and techniques involved in finding derivatives. By practicing with these solutions, students can improve their problem-solving skills and prepare effectively for exams.
How can NCERT Solutions for Chapter 13 Exercise 13.3 benefit students?
NCERT Solutions help students understand the concepts and techniques involved in finding derivatives, improve their problem-solving skills, and prepare effectively for exams.
Where can I find NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3?
NCERT Solutions for Chapter 13 Exercise 13.3 can be found on Physics Wallah.
Are NCERT Solutions for Class 12 Maths Chapter 13 Exercise 13.3 sufficient for exam preparation?
Yes, NCERT Solutions provide comprehensive coverage of the exercise, making them sufficient for exam preparation. However, students may also benefit from additional practice and reference materials for a more thorough understanding.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.