The definition of congruent triangles states that two triangles are congruent if and only if all their sides and angles match. This means that if all the sides and angles of one triangle are equal to the corresponding sides and angles of another triangle, then the triangles are congruent.
Sufficient Condition for Triangle Congruence
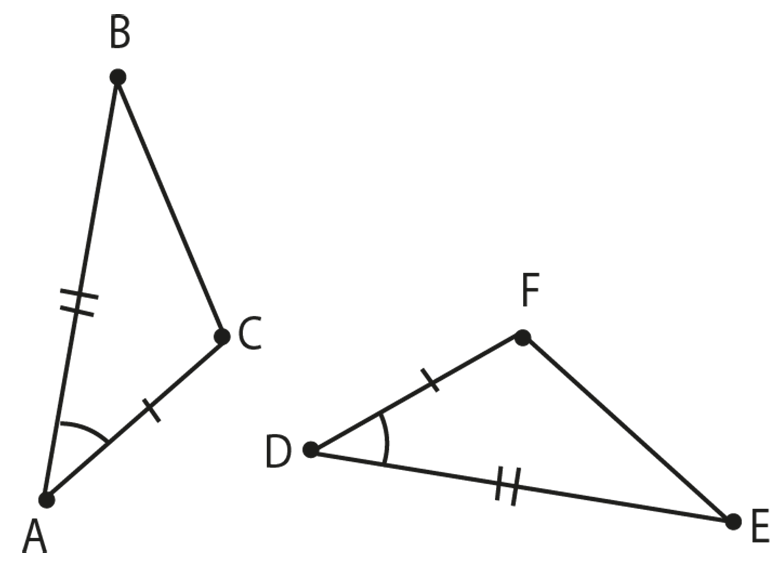
In the activity comparing triangles ΔABC and ΔDEF, we observed that when two sides and the included angle of one triangle match those of another, the triangles are congruent. This principle is known as the Side-Angle-Side (SAS) congruency condition. It simplifies the process of determining triangle congruence by requiring only three conditions to be met instead of all six.
Theorem 9
"Two triangles are congruent if any two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle".
In the two given triangles,
Δ
ABC
ΔABC
and
Δ
DEF
ΔDEF
,
AB = DE
AB = DE
AC = DF
AC = DF
and
∠
BAC =
∠
EDF
∠BAC = ∠EDF
.
To prove:
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Proof:
If we rotate and drag
Δ
ABC
ΔABC
on
Δ
DEF
ΔDEF
, such the vertices B falls on the vertex of the other triangle E and place BC along EF, we will find that, since
AB = DE
AB = DE
, C falls on F.
Also,
∠
B =
∠
E
∠B = ∠E
.
AB falls on DE, A will coincide with the vertex D and C with F.
So, AC coincides with DF.
∴
Δ
ABC
∴ΔABC
coincides with
Δ
DEF
ΔDEF
.
∴
Δ
ABC
≅
Δ
DEF
Application of SAS Congruency
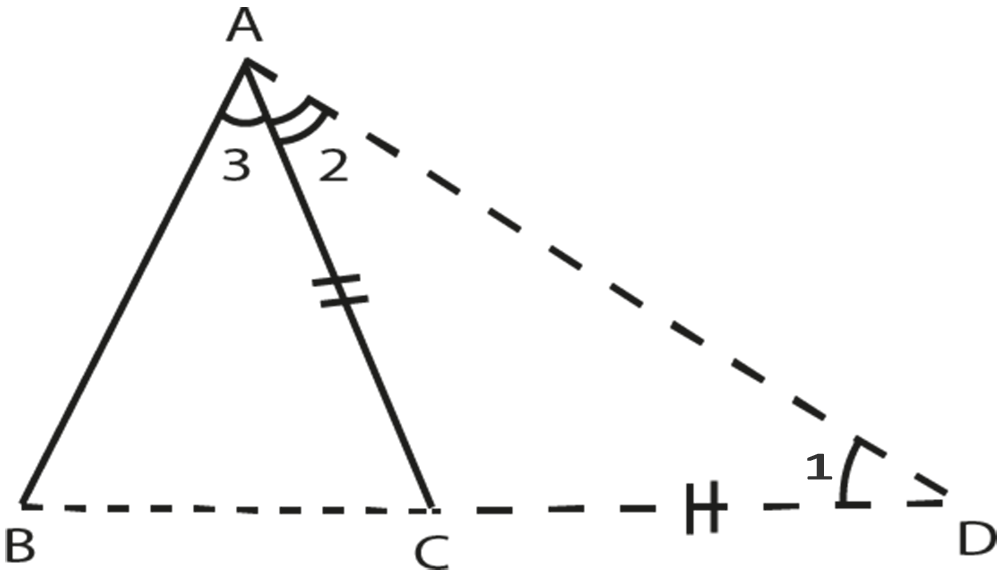
In this figure we cannot apply SAS as the given data is not sufficient. On the basis of angles and sides, the SAS congruency criterion defines the relationship between two triangles. As a result, here we cannot say if AC is the angle bisector of
∠
A
∠A
, hence we cannot determine if the two triangles that may be shown are congruent.
Theorem 10
"Angles opposite to equal sides are equal".
In
Δ
ABC
ΔABC
,
AB = AC
AB = AC
To prove:
∠
ABC =
∠
ACB
∠ABC = ∠ACB
Construction: Draw the angle bisector of A, AD.
Proof:
Comparing both the triangles,
Given that
AB = AC
AB = AC
AD is the common side.
∠
BAD =
∠
DAC
∠BAD = ∠DAC
(as AD is the angle bisector)
∴
Δ
BAD =
Δ
DAC
∴ΔBAD = ΔDAC
(by SAS congruency rule)
∴
∠
ABD =
∠
ACD
∴∠ABD = ∠ACD
(by CPCT)
∴
∠
B =
∠
C
∴∠B = ∠C
Hence, proved.
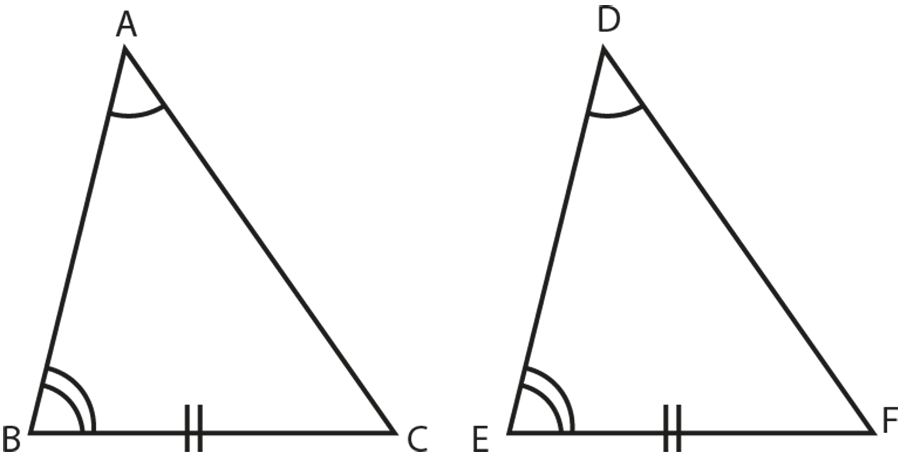
ASA Congruence Condition
The Angle-Side-Angle (ASA) congruence condition states that two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. This condition simplifies the process of determining triangle congruence by requiring the equality of two angles and the side between them, thereby ensuring that the triangles have the same shape and size.
Theorem 11
Given:
In
Δ
ABC
ΔABC
and
Δ
DEF
ΔDEF
,
∠
B =
∠
E
∠B = ∠E
and
∠
C =
∠
F
∠C = ∠F
BC = EF
BC = EF
.
To prove:
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Proof:
There are three possibilities
Case I:
AB = DE
AB = DE
Case II:
AB DE
AB DE
Case III:
AB DE
AB DE
Case I: In addition to data, if
AB = DE
AB = DE
then
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
(by SAS congruence postulate)
Case II: If
AB DE
AB DE
and let K is any point on DE such that
EK = AB
EK = AB
.
Join KF.
Now compare triangles ABC and KCF.
BC = EF
BC = EF
(given)
∠
B =
∠
E
∠B = ∠E
(given)
Let
AB = EK
AB = EK
Δ
ABC
≅
Δ
KEF
ΔABC ≅ ΔKEF
(SAS criterion)
Hence,
∠
ABC =
∠
KEF
∠ABC = ∠KEF
But,
∠
ABC =
∠
DEF
∠ABC = ∠DEF
(given)
Hence, K coincides with D.
Therefore, AB must be equal to DE.
Case III: If
AB DE
AB DE
, then a similar argument applies.
AB must be equal to DE.
Hence the only possibility is that AB must be equal to DE and from SAS congruence condition
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Hence the theorem is proved.
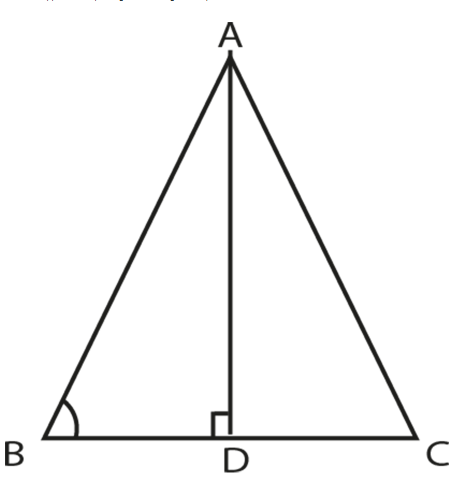
Theorem 12
"In a triangle the sides opposite to equal angles are equal".
This theorem can also be stated as
"The sides opposite to equal angles of a triangle are equal".
Given:
In
Δ
ABC
,
∠
B =
∠
C
ΔABC, ∠B = ∠C
To prove:
AB
¯¯¯¯¯¯¯
=
AC
¯¯¯¯¯¯¯
AB¯ = AC¯
Construction:
Draw
AD
¯¯¯¯¯¯¯¯
⊥
BC
¯¯¯¯¯¯¯
AD¯ ⊥ BC¯
Proof:
Construct two right angle triangles, ADB and ADC, right angled at D.
Here,
Δ
ABC
,
∠
B =
∠
C
ΔABC, ∠B = ∠C
∠
ADB =
∠
ADC = 90
∘
∠ADB = ∠ADC = 90∘
(from the construction)
AD
¯¯¯¯¯¯¯¯
AD¯
is common for both the triangles.
∴
Δ
ADB
≅
Δ
ADC
∴ΔADB ≅ ΔADC
(by ASA postulate)
AB
¯¯¯¯¯¯¯
=
AC
¯¯¯¯¯¯¯
AB¯ = AC¯
(corresponding sides)
AAS Congruence Condition
The Angle-Angle-Side (AAS) congruence condition states that two triangles are congruent if two angles and a non-included side of one triangle are equal to the corresponding two angles and the side of the other triangle. This condition provides another method for determining triangle congruence by requiring the equality of two angles and a side not included between them, ensuring that the triangles have the same shape and size.
Given:
In triangles ABC and DEF,
BC = EF
BC = EF
(non-included sides)
∠
B =
∠
E
∠B = ∠E
∠
A =
∠
D
∠A = ∠D
To prove:
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Proof:
∠
B =
∠
E
∠B = ∠E
(given)
∠
A =
∠
D
∠A = ∠D
(given)
Now, adding both,
∠
A +
∠
B =
∠
E +
∠
D
∠A +∠B = ∠E +∠D
…(1)
Since,
∠
A +
∠
B +
∠
C =
∠
E +
∠
D+
∠
F = 180
∘
∠A +∠B +∠C = ∠E +∠D+∠F = 180∘
, considering (1) we can say that,
∠
C =
∠
F
∠C = ∠F
…(2)
Now in triangle ABC and DEF,
∠
B =
∠
E
∠B = ∠E
(given)
∠
C =
∠
F
∠C = ∠F
(proved in (2))
BC = EF
BC = EF
(given)
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
(by SAS congruency)
SSS Congruence Condition
"Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle".
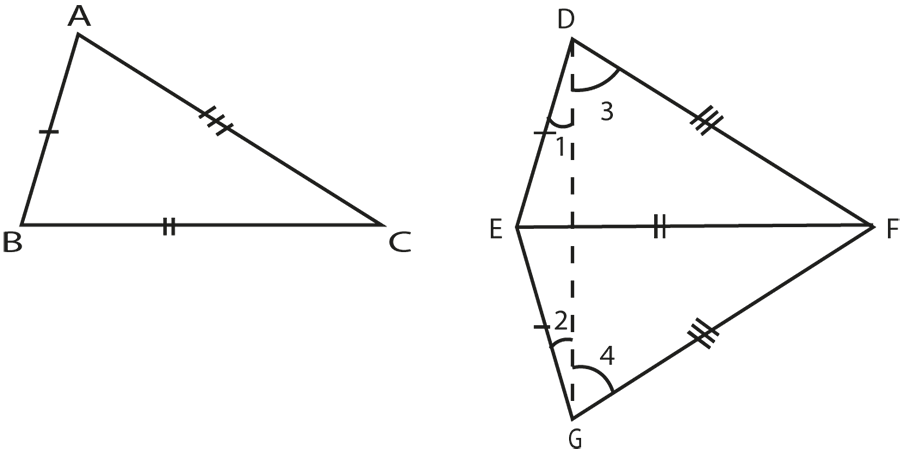
Given:
In triangles ABC and DEF,
AB = DE
AB = DE
BC = EF
BC = EF
AC = DF
AC = DF
Note:
Let BC and EF be the longest sides of triangles ABC and DEF respectively.
To prove:
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Construction: If BC is the longest side, draw EG such that
EG = AB
EG = AB
and
∠
GEF =
∠
ABC
∠GEF = ∠ABC
.
Join GF and DG.
Proof:
In triangles ABC and GEF,
AB = GE
AB = GE
(by construction)
BC = EF
BC = EF
(given)
∠
ABC =
∠
GEF
∠ABC = ∠GEF
(by construction)
∴
Δ
ABC =
Δ
GEF
∴ΔABC = ΔGEF
(SAS congruence condition)
∠
BAC =
∠
EGF
∠BAC = ∠EGF
(by CPCT)
and
AC = GF
AC = GF
(by construction)
But
AB = DE
AB = DE
(given)
∴
DE = GE
∴DE = GE
Similarly,
DF = GF
DF = GF
In
Δ
EDG
ΔEDG
,
DE = GE
DE = GE
(Proved)
∴
∠
1
=
∠
2
∴∠1=∠2
…(1) (angles opposite equal sides)
In
Δ
EGF
ΔEGF
,
DF = GF
DF = GF
(Proved)
∴
∠
3
=
∠
4
∴∠3=∠4
…(2) (angles opposite equal sides)
By adding (1) and (2), we get,
∴
∠
1
+
∠
3
=
∠
4
+
∠
2
∴∠1+∠3=∠4+∠2
∠
EDF =
∠
EGF
∠EDF = ∠EGF
but we have proved that
∠
BAC =
∠
EGF
∠BAC = ∠EGF
Therefore,
∠
EDF =
∠
BAC
∠EDF = ∠BAC
Now in triangles ABC and DEF,
AB = DE
AB = DE
(given)
AC = DF
AC = DF
(given)
∠
EDF =
∠
BAC
∠EDF = ∠BAC
(proved)
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
(by SAS congruency)
Theorem of RHS (Right Angle Hypotenuse Side) Congruence
If the hypotenuse and one side of one triangle are equal to the hypotenuse and corresponding side of the other triangle, the two triangles are congruent.
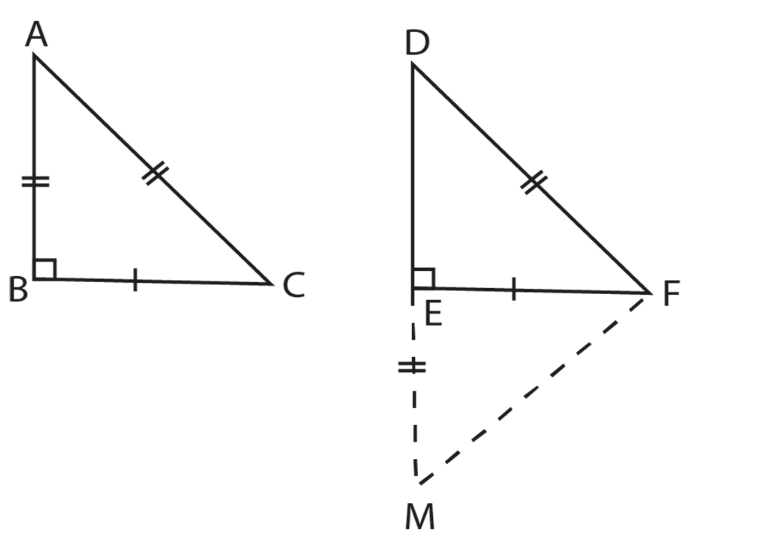
Given:
ABC and DEF are two right-angled triangles such that
-
∠
B =
∠
E = 90
∘
∠B = ∠E = 90∘
-
Hypotenuse
AC
¯¯¯¯¯¯¯¯¯
=
AC ¯ =
Hypotenuse
DF
¯¯¯¯¯¯¯
DF¯
and
-
Side
BC
¯¯¯¯¯¯¯¯
=
BC ¯=
Side
EF
¯¯¯¯¯¯¯
EF¯
To prove:
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
Construction
Produce DE to M so that
EM = AB
EM = AB
. Join MF.
Proof:
In triangles ABC and MEF,
EM = AB
EM = AB
(construction)
BC = EF
BC = EF
(given)
∠
ABC =
∠
MEF = 90
∘
∠ABC = ∠MEF = 90∘
Therefore,
Δ
ABC
≅
Δ
MEF
ΔABC ≅ ΔMEF
(SAS congruency)
Hence,
∠
A =
∠
M
∠A = ∠M
…(1) (by CPCT)
AC
¯¯¯¯¯¯¯
=
MF
¯¯¯¯¯¯¯¯
AC¯=MF¯
…(2) (by CPCT)
Also,
AC = DF
AC = DF
… (3) (given)
From (1) and (3),
DF = MF
DF = MF
Therefore,
∠
D =
∠
M
∠D = ∠M
...(4) (Angles opposite to equal sides of
Δ
DFM
ΔDFM
)
From (2) and (4),
∠
A =
∠
D
∠A = ∠D
…(5)
Now compare triangles ABC and DEF,
∠
A =
∠
D
∠A = ∠D
(from 5)
∠
B =
∠
E = 90
∘
∠B = ∠E = 90∘
(given)
∴
∠
C=
∠
F
∴∠C=∠F
…(6)
Compare triangles ABC and DEF,
BC
¯¯¯¯¯¯¯
=
EF
¯¯¯¯¯¯¯
BC¯=EF¯
(given)
AC
¯¯¯¯¯¯¯
=
DF
¯¯¯¯¯¯¯
AC¯=DF¯
(given)
∠
C=
∠
F
∠C=∠F
(from 6)
Therefore,
Δ
ABC
≅
Δ
DEF
ΔABC ≅ ΔDEF
(by SAS congruency)
Inequality of Angles
Here we can see that, both these angles are not equal, as
135
∘
<
160
∘
135∘<160∘
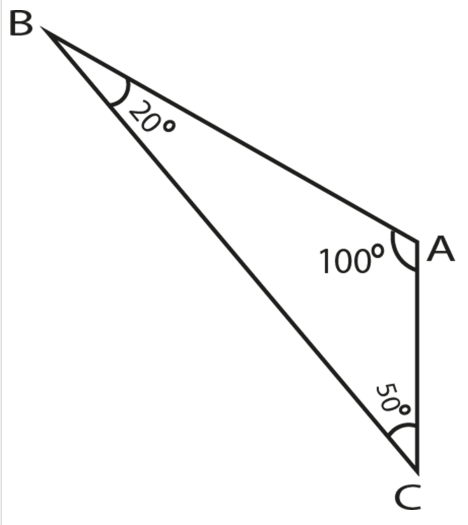
Inequality in a Triangle
Construct a triangle ABC as shown in the figure.
Observe that in triangle ABC,
AC
¯¯¯¯¯¯¯
AC¯
is the smallest side (2 cm)
B is the angle opposite to
AC
¯¯¯¯¯¯¯
AC¯
and
∠
B = 20
∘
∠B = 20∘
BC
¯¯¯¯¯¯¯
BC¯
is the greatest side (6 cm)
A is the angle opposite to
BC
¯¯¯¯¯¯¯
BC¯
and
∠
A = 100
∘
∠A = 100∘
From the measurements made above of side and angle opposite to it, we can write the relation in the form of a statement.
"If two sides of a triangle are unequal then the longer side has the greater angle opposite to it”.
Theorem on Inequalities
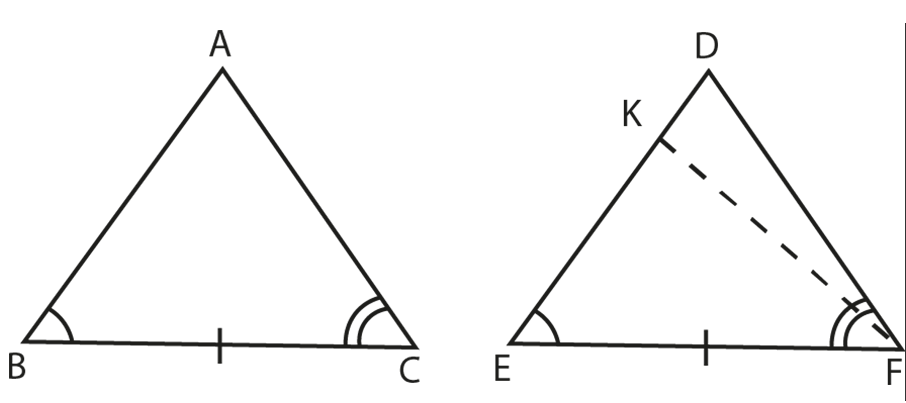
Theorem 1:
If two sides of a triangle are unequal, the longer side has the greater angle opposite to it.
Read the statement and draw a triangle as per data.
Draw
Δ
ABC
ΔABC
, such that
AC AB
AC AB
.
Data:
AC AB
AC AB
To Prove:
∠
ABC =
∠
ACB
∠ABC = ∠ACB
Construction:
Take a point D on
AC
¯¯¯¯¯¯¯
AC¯
such that
AB
¯¯¯¯¯¯¯
=
AD
¯¯¯¯¯¯¯¯
AB¯ = AD¯
. Join B to D.
Proof:
In
Δ
ABC
ΔABC
,
AB
¯¯¯¯¯¯¯
=
AD
¯¯¯¯¯¯¯¯
AB¯ = AD¯
(by construction)
∴
∠
ABD =
∠
ADB
∴∠ABD = ∠ADB
…(1)
but
∠
ADB
∠ADB
is the exterior angle with reference to
Δ
DBC
ΔDBC
.
∠
ADB
∠
DCB
∠ADB ∠DCB
… (2)
From relation (1) and (2) we can write
∠
ABD
∠
DCB
∠ABD ∠DCB
But
∠
ABD
∠ABD
is a part of
∠
ACB
∠ACB
.
∴
∠
ACB
∠
DCB
∴∠ACB ∠DCB
or
∴
∠
ABC
∠
ACB
∴∠ABC ∠ACB
Hence, proved.
Angle Side Relation
Theorem 2:
In a triangle, if two angles are unequal, the side opposite to greater angle is longer than the side opposite to the smaller angle.
Theorem 3
In a triangle, the greater angle has the longer side opposite to it.
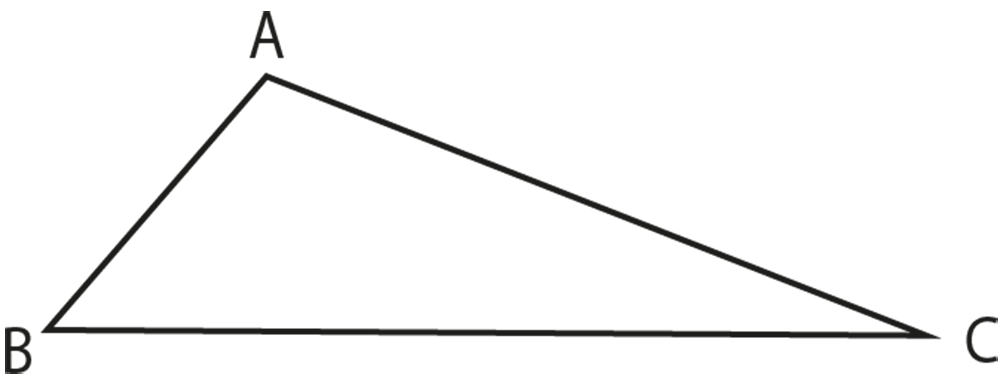
Given:
In
Δ
ABC
ΔABC
,
∠
ABC
∠
ACB
∠ABC ∠ACB
To prove:
AC AB
AC AB
Proof:
In
Δ
ABC
ΔABC
, AB and AC are two line segments. So the following are the three possibilities of which
exactly one must be true.
-
either
AB = AC
AB = AC
, then
∠
B =
∠
C
∠B = ∠C
which is contrary to the hypothesis.
∴
AB
≠
AC
∴AB ≠ AC
-
AB AC
AB AC
, then
∠
B
∠
C
∠B ∠C
which is contrary to the hypothesis.
-
AB AC
AB AC
, this is the only condition we are left with, so
AB AC
AB AC
must be true.
Hence, proved.
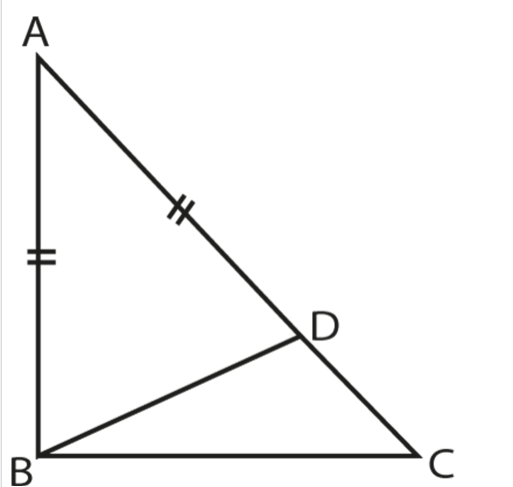
Theorem 4
Prove that in any triangle the sum of the lengths of any two sides of a triangle is greater than the length of its third side.
Draw
Δ
ABC
Δ ABC
.
Data:
ABC is a triangle.
To prove:
AB
¯¯¯¯¯¯¯
+
AC
¯¯¯¯¯¯¯
>
BC
¯¯¯¯¯¯¯
AB¯+AC¯>BC¯
AB
¯¯¯¯¯¯¯
+
BC
¯¯¯¯¯¯¯
>
AC
¯¯¯¯¯¯¯
AB¯+BC¯>AC¯
AC
¯¯¯¯¯¯¯
+
BC
¯¯¯¯¯¯¯
>
BA
¯¯¯¯¯¯¯
AC¯+BC¯>BA¯
Construction:
Produce
BC
¯¯¯¯¯¯¯
BC¯
to D such that
AC
¯¯¯¯¯¯¯
=
CD
¯¯¯¯¯¯¯
AC¯ = CD¯
. Join A to D.
Proof:
AC
¯¯¯¯¯¯¯
=
CD
¯¯¯¯¯¯¯
AC¯ = CD¯
(by construction)
∠
1
=
∠
2
∠1=∠2
…(1)
From the figure,
∠
BAD =
∠
2+
∠
3
∠BAD = ∠2+∠3
…(2)
∠
BAD
∠
2
∠BAD ∠2
∴
∠
BAD
∠
1
∴∠BAD ∠1
(proved from 1)
AB
¯¯¯¯¯¯¯
AB¯
is opposite to
∠
1
∠1
and
BD
¯¯¯¯¯¯¯
BD¯
is opposite to
∠
BAD
∠BAD
.
In
Δ
BAD
ΔBAD
,
∠
1
∠
2+
∠
3
∠1 ∠2+∠3
BD AB
BD AB
(side opposite to greater angle is greater)
From figure
BD = BC + CD
BD = BC + CD
∴
BC + CDAB
∴BC + CDAB
∴
BC + ACAB
∴BC + ACAB
Since,
CD = AC
CD = AC
, hence, sum of two sides of a triangle is greater than the third side.
Similarly,
AB
¯¯¯¯¯¯¯
+
BC
¯¯¯¯¯¯¯
>
AC
¯¯¯¯¯¯¯
AB¯+BC¯>AC¯
and
AC
¯¯¯¯¯¯¯
+
BC
¯¯¯¯¯¯¯
>
BA
¯¯¯¯¯¯¯
AC¯+BC¯>BA¯
.
Hence, proved.
Theorem 5
Of all the line segments that can be drawn to a given line, from a point not lying on it, the perpendicular line segment is the shortest.
l
𝑙
is a line and P is a point not lying on it.
PM
⊥
l
PM⊥𝑙
. N is any point on l other than M.
To prove:
PM PN
PM PN
Proof:
In
Δ
PMN
Δ PMN
,
∠
M
∠M
is the right angle.
∴
∠
N
∴∠N
is an acute angle, from angle sum property.
∵
∠
M
∠
N
∵∠M ∠N
PN PM
PN PM
(side opposite to greater angle)
∴
PMPN
∴PMPN
.
Benefits of CBSE Class 9 Maths Notes Chapter 7 Triangles
-
Concept Clarity
: These notes provide clear explanations of various concepts related to triangles, making it easier for students to understand the fundamentals.
-
Structured Learning
: The notes follow a structured format, covering each topic comprehensively, ensuring that students don't miss out on any essential concepts.
-
Exam Preparation
: The notes include important formulas, theorems, and properties related to triangles, which are crucial for exam preparation. Students can use these notes for quick revision before exams.
-
Visual Aid:
Diagrams and illustrations included in the notes help students visualize geometric concepts and understand them better.

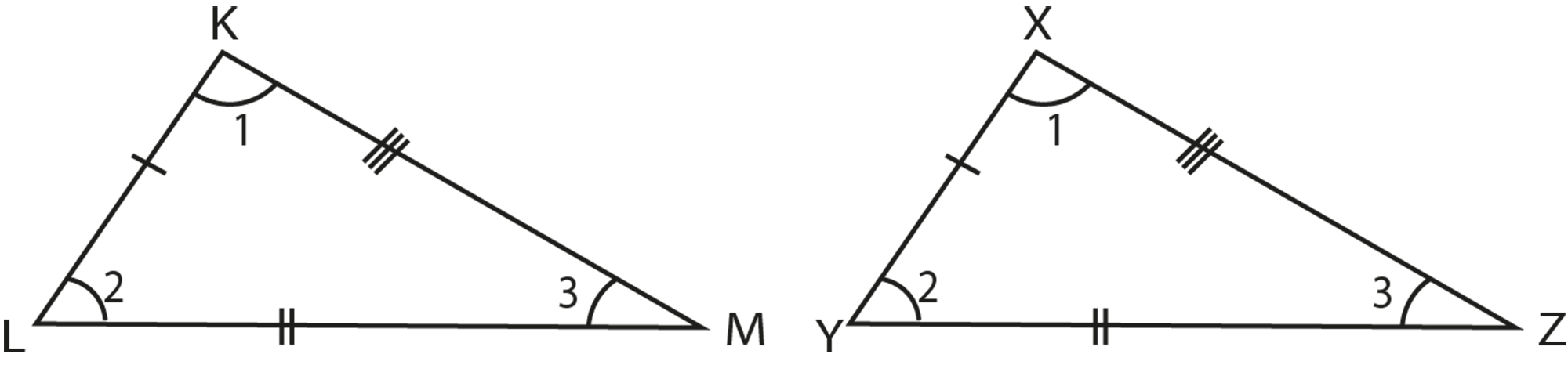 Consider triangles KLM and XYZ. When you align one on top of the other, they match perfectly, indicating congruency. Both triangles have congruent angles and sides: KL ≅ XY, LM ≅ YZ, and KM ≅ XZ.
For two triangles to be congruent, all three angles and three sides of one triangle must match the corresponding angles and sides of the other triangle.
Consider triangles KLM and XYZ. When you align one on top of the other, they match perfectly, indicating congruency. Both triangles have congruent angles and sides: KL ≅ XY, LM ≅ YZ, and KM ≅ XZ.
For two triangles to be congruent, all three angles and three sides of one triangle must match the corresponding angles and sides of the other triangle.

 For example, in Figure line segments AB and CD are congruent because they have the same length.
For example, in Figure line segments AB and CD are congruent because they have the same length.
 In Figure angles a and b, as well as angles m and n, are congruent because they share the same measure.Angles m and n are considered congruent as they are vertically opposite angles.
In Figure angles a and b, as well as angles m and n, are congruent because they share the same measure.Angles m and n are considered congruent as they are vertically opposite angles.