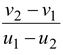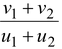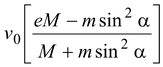Collision

Collision is a brief event between objects that contact each other. The interaction between two or more objects is called a collision if there exists three identifiable stages to this interaction: before, during and after. In the before and after stage the interaction forces are zero or approaches zero asymptotically. Between these two states the interaction forces are large and often the dominating forces governing the object’s motion. The magnitude of the interacting force is often unknown. Therefore, the conservation of momentum statement is useful for relating the initial velocities before the interaction to the final velocities after the interaction without requiring a detailed knowledge of the interaction forces.

Types of Collision

Collisions may be either elastic or inelastic. Linear momentum is conserved in both cases. A perfectly elastic collision is defined as one in which the total kinetic energy of the particles is also conserved.

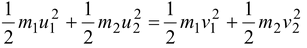     (9.12)

In an inelastic collision, the total kinetic energy of the particle changes. Some of the kinetic energy is stored as potential energy associated with a change in internal structure or state, and is not immediately recovered. Some of the energy may be used to raise the system (e.g. an atom) to a state with higher energy. Or, it may be converted into thermal energy of vibrating atoms and molecules or into light, sound or some other form of energy.

In a completely inelastic collision, the two bodies couple or stick together.

Coefficient of Restitution (e)

The elasticity of collision may be measured in terms of a dimensionless parameter called the coefficient of restitution (e).

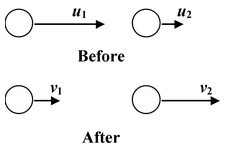
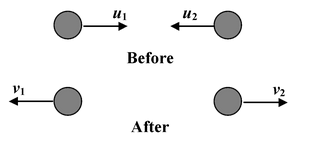
It is defined as the ratio of velocity of separation to the velocity of approach of the two colliding bodies

e = 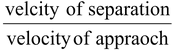     (9.13)

For an elastic collision e = 1

For an inelastic collision 0 < e < 1

For completely inelastic collision: e = 0

Elastic Collision in One Dimension

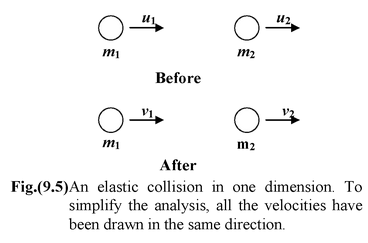
Figure (9.5) shows a one - dimensional elastic collision between two balls.

Applying momentum conservation,

P_i = P_f

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

orm1(u₁- v₁) = m₂(v₂ – u₂) (9.14)

Taking e = 1, velocity of separation = velocity of approach

v₂ – v₁ = u₁- u₂(9.15)

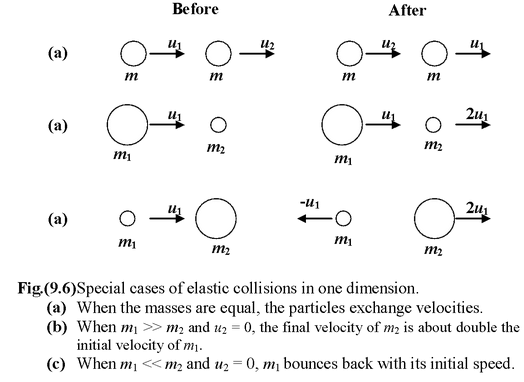
Let us consider two special cases of collisions:

First, when the particles have equal mass, and second when one of them, say m2, is initially at rest.

(i)Equal masses: m₁ = m₂ = m

Equation (9.14) takes the form u₁ + u₂ = v₁ + v₂,

Solving equations (9.14) and ( 9.15), we get

v₁ = u₂ and v₂ = u₁

(ii)Unequal masses m1 ≠ m2. Target at Rest: u2 = 0

Equation (9.14) becomes m1u1 = m₁v₁ + m₂v₂, and equation (9.15) is u1 = -v1 + v2.

After solving, we get

v1 = 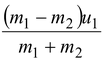(9.16)

v2 = 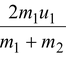(9.17)

(a)When m₁ >> m₂, we may ignore the mass of m2in comparison with m1. This lead to

v₁ = u1and v₂ = 2u₁, which means that m1maintains its initial velocity u1but it imparts double this value to m2.

(b)When m1 << m₂ we may ignore m1in comparison with m2. We then find that v1 = -u1and v2= 0. Thus, m1reverses its velocity, leaving m2 essentially unmoved as in figure(9.6).

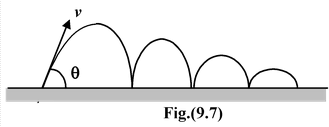
Example 9.7

(b) the total horizontal distance covered before the particle stops bouncing.

Solution

After first impact, let v1 and θ1 be the velocity and angle of rebound, as shown in the figure.

Nowv1cosθ₁ = v cosθ

v1sinθ₁ = evsinθ

Similarly, after second impact

v₂cosθ₂ = v₁cosθ₁

v2sinθ₂ = ev1sinθ₁ and so on.

(a)The total time of flight is

Example 9.8

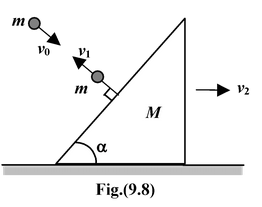
A wedge of mass M and angle α can move freely on a smooth horizontal plane. A smooth sphere of mass m strikes it in a direction perpendicular to its inclined face and rebounds. If the coefficient of restitution is e, then find the ratio of the speeds of the sphere just before and just after the impact.

Solution