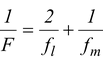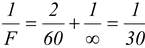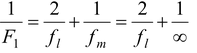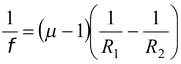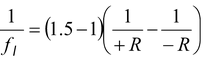Lenses
Optics of Class 12
A lens is a transparent polished body bounded on two sides by curved surfaces. In particular, one of the surfaces maybe plane.
Spherical lenses have spherical surfaces as bounds.
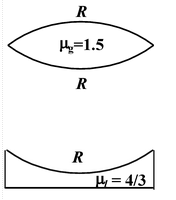
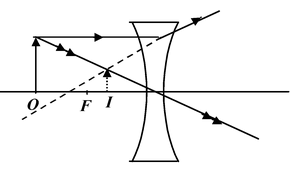
Converging lenses convert a parallel beam of incident rays into a convergent beam. Converging lenses are convex, i.e. such that the thickness at the middle is larger than the thickness of edges.
They include convexo-convex, plano-convex, and cancavo-convex lenses (fig.(15.48)).
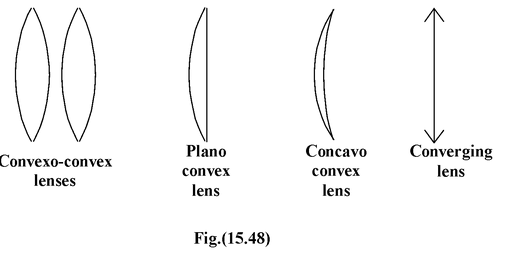
Diverging lenses convert a parallel beam of rays into a divergent beam. Diverging lenses are concave, i.e. such that the thickness at their edges is larger than the thickness at the middle. They include concavo-concave, plano-concave, and convexo-concave lenses (Fig.(15.49)).

Example 15.15
An object is placed 45 cm from a converging lens of focal length 30 cm. A mirror of radius 40 cm is to be placed on the other side of lens so that the object coincides with its image.
Find the position of the mirror if it is
(a) convex ?
(b)concave?
Solution
(a)The object and image will coincide only if the light ray retraces its path and it will happen only when the ray normally strike the mirror. In other words the centre of the curvature of the mirror and the rays incident on the mirror are collinear.
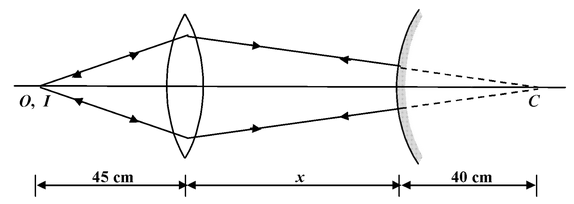
The rays after refraction from lens must be directed towards the centre of curvature of mirror at C. If x is the separation, then for the lens
u = −45 cm, v = x + 40, f = 30 cm
Using lens formula 1/v - 1/u = 1/f
or
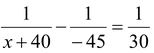
or x =
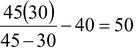 cm
cm
(b)
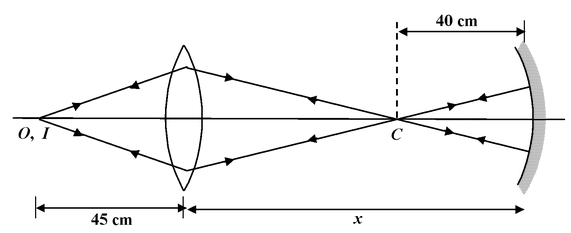
In case of concave mirror, the refracted rays from lens meets at C, the centre of curvature (C) of the mirror.
Using lens formula 1/v - 1/u = 1/f
u = -45 cm, v = x – 40, f = 30 cm
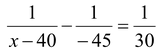
or x – 40 = (45)x 30/45-30
or x = 90 + 40 = 130 cm
Power of a Lens
Power of a lens is defined as P = μ/f where μ is the refractive index of the medium and f is the focal length of the lens in that medium. The unit of power is dioptre.
Example 15.16
A lens has a power of +5 diopter in air. What will be its power if completely immersed in water? Given μ g = 3/2 ; μ w = 4/3 .
Solution
Let f a and f w be the focal lengths of the lens in air and water respectively, then
P
a
=
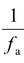 and P
w
=
and P
w
=
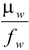
f a = 0.2 m = 20 cm
Using lensmaker’s formula
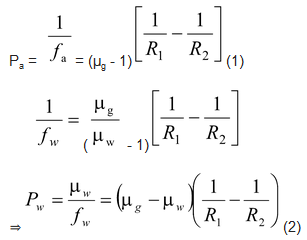
Dividing equation (2) by equation (1), we get,
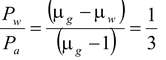
or P w = P a /3 = +5/3 D
Related Topics
Displacement Method:
In this method, an object and a screen are placed at a distance a apart. A convex lens of focal length f (f < a/4 ) can be placed in two positions between the object and the screen such that a real image of the object is formed on the screen in both the positions.
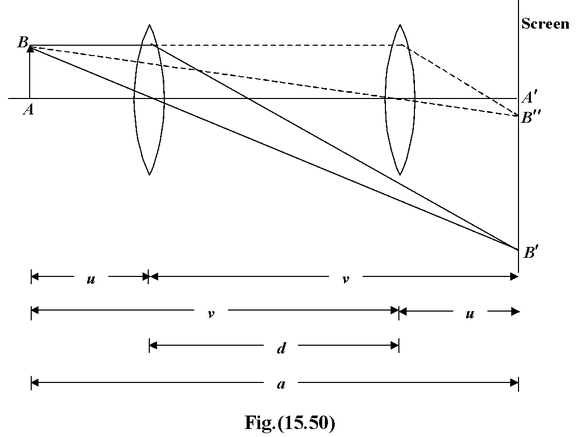
Let a be the distance between the object and the screen and let d be the distance between the two position of the lens. From the figure
u + v = a
v – u = d
Solving, we get v = a+d/2 , u = a-d/2 .
Using the lens formula and simplifying, we get
f = a 2 - d 2 /4a (15.25)
Let I 1 = A′B′; I 2 = A′B′′; O = AB
m
1
=
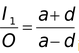 i.e. one image is larger than the object.
i.e. one image is larger than the object.
m
2
=
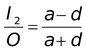 i.e. the other image is shorter than the object.
i.e. the other image is shorter than the object.
∴m
1
m
2
=
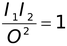
⇒O =
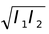 (15.26)
(15.26)
i.e. the size of the object is the geometric mean of the sizes of the two image.
Example 15.17
For two positions of a converging lens between an object and a screen which are 96 cm apart, two real images are formed. The ratio of the lengths of the two images is 4.84. Calculate the focal length of the lens.
Solution
Here m1/m2 = 4.84
⇒ (a+d/a-d) 2 4.84 ⇒ a+d/a-d - 2.2/1
Putting a = 96 cm gives d = 36 cm
∴ f = a 2 - d 2 /4a = 20625 cm
Example 15.18
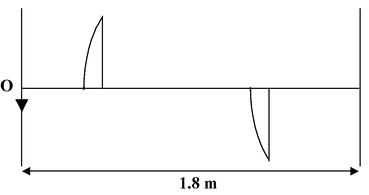
A thin plano-convex lens of focal length f is split into two halves. one of the halves is shifted along the optical axis. The separation between object and image planes is 1.8 m. The magnification of the image formed by one of the half-lenses is 2. Find the focal-length of the lens and separation between the two halves.
Solution
This is a modified displacement method problem.
Herea = 1.8 m and a+d/a-d = 2/1
Solving gives d = 0.6 m
∴f = a 2 - d 2 /4a = 0.4 m
Equivalent Focal Length of Lens Combination
If n number of lenses of focal lengths f 1 , f 2 , f 3 ,…f n are joined together then the equivalent focal length of the combination is given by
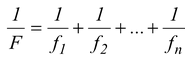 (15.27)
(15.27)
In terms of power P = p 1 + p 2 + … + p n
Sign Convention
Focal length of converging lens is taken as positive and that of the diverging lens is taken as negative.
Example 15.19
A convergent lens of 6 diopters is combined with a diverging lens of -2 diopters. Find the power and focal length of the combination.
Solution
HereP 1 = 6 diopter, P 2 = -2 diopter
Power of the combination is given by
Using the formula P = P 1 + P 2 = 6 - 2 = 4 diopters
f = 1/P = 1/4 = 0.25 m = 25 cm
Equivalent Focal Length of Lens Mirror Combination
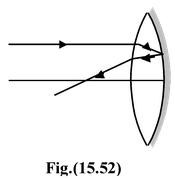
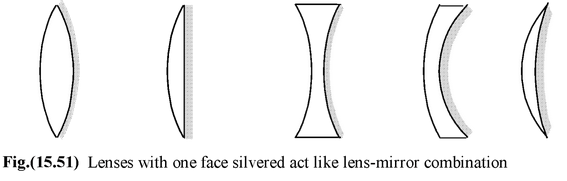
When one face of a lens is silvered as shown in figure (15.51) it acts like a lens-mirror combination.
|
It is obvious from the ray diagram as shown in figure (15.52) that the incident ray of light is refracted through the lens twice (i.e., once when light is incident on the lens and second time when reflected by the mirror) and reflected from the mirror once. |
|
The combination acts like a mirror whose equivalent focal length is given by
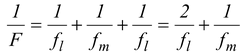 (15.28)
(15.28)
wheref l = focal length of lens and
f 2 = focal length of mirror
Sign Convention
Focal length of converging lens or mirror is positive; and that of diverging lens or mirror is negative.
Example 15.20
One face of an equiconvex lens of focal length 60 cm made of glass (μ = 1.5) is silvered . Does it behave like a concave mirror or convex mirror.
Solution
Applying lens makers formula, the radius of curvature of the equiconvex lens
From equation (15.28).
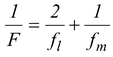
heref l = +60cm (converging lens)
f m = +R/2 = +30 (converging mirror)
∴
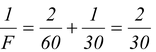
The positive sign indicates that the resulting mirror is converging or concave.
Example 15.21
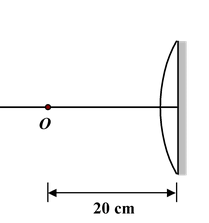
The plane surface of a plano-convex lens of focal length 60cm is silver plated. A point object is placed at a distance 20cm from the convex face of lens. Find the position and nature of the final image formed.
|
Solution Using equation (15.28)
here, f l = + 60 cm; f m = ∞
∴
orF = +30 cm The problem is reduced to a simple case where a point object is placed in front of a concave (converging) mirror. Using mirror formula |
|
1/v - 1/u = 1/f
hereu = −20 cm; f = −30cm
∴ 1/v + 1/20 = 1/-30
thusv = 60 cm.
The image is erect and virtual.
Example 15.22
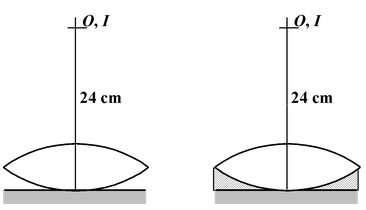
An equiconvex lens is placed on a plane mirror. An object coincides with its image when it is at a height of 24 cm from the lens. The gap between the lens and the mirror is filled with water (μ w = 4/3). By how much distance should the object be now shifted so that it again coincides with its image? (μ g = 1.5)
|
Solution Let F 1 be equivalent focal length of the lens-mirror combination 2F 1 = 24 F 1 = 12 cm
1/12 = 2/f l f l = focal length of lens = 24 cm |
|
When water is filled, we have a combination of glass-lens, water-lens and a plane mirror.
Let F 2 be the equivalent focal length, then
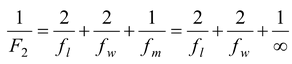
or
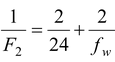 (1)
(1)
|
Applying lens maker’s formula
glass lens:
1/24 = 1/2 x (2/R) R =24 cm |
|
Water lens
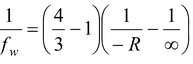
1/f w = -1/3 x (1/R)
f w = -72 cm
Substituting the value of f w in equation (1)
1/F 2 = 2/24 + 2/-72
F 2 = 18 cm
2F 2 = 36 cm
Shift, s = (36 – 24) cm = 12 cm upwards
The object will coincide with the image at a height of 36 cm from the lens and hence it should be shifted 12 cm upwards.
Table 15.2 Position and nature of image formed for a given position of object.
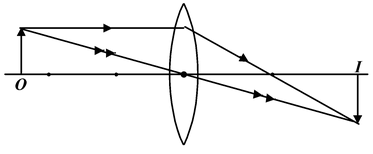
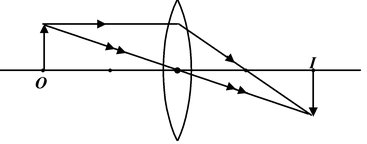
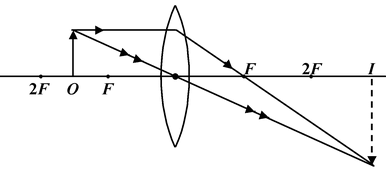
(a) For convergent Convex Lens
|
S.No. |
Position of Object |
Ray-Diagram |
Details of Image |
|
1. |
At infinity |
|
Real inverted, Diminished (m << -1) at F |
|
2. |
Between ∞ and 2F |
|
Real, inverted , diminished (m < -1) between F and 2F |
|
3. |
At 2F |
|
Real, inverted, Equal m = -1 at 2F |
|
4. |
Between 2F and F |
|
Real, inverted, Enlarged (m > -1) between 2F and ∞ |
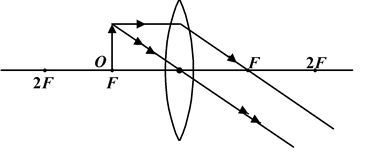
|
5. |
At F |
|
Real, inverted, Enlarged (m >> -1) At infinity. |
|
6. |
Between F and O |
|
Virtual Erect Enlarged (m >> -1) |
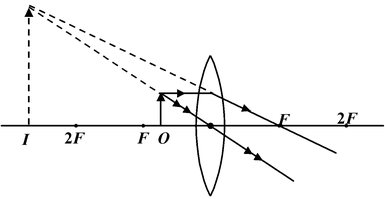
(b)For Divergent or Concave Lens
|
S.No. |
Position of Object |
Ray-Diagram |
Details of Image |
|
1. |
At infinity |
|
Real inverted, very small (m << -1), at F |
|
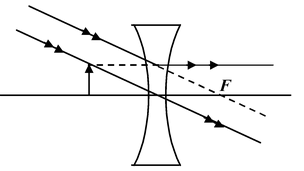
2. |
Infront of Lens |
|
Virtual, erect Diminished (m < +1) Between F and optical centre |