
M. Curie and P. Curie with Becquerel, were awarded the Nobel Prize in Physics for their discovery of Radioactivity, in 1903.
Radioactivity is the phenomenon of spontaneous disintegration, attended by emission of electromagnetic radiations, of heavy atomic nuclei like Uranium, Radium, etc. at a constant rate unaffected by any physical or chemical changes or influences such as temperature, pressure, etc. to which the atom may be subjected. It is a nuclear property of the active element and in all radioactive processes. There are three features of radioactivity from the perspective of classical physics:- When a nucleus undergoes alpha or beta decay, its atomic number Z changes and it becomes the nucleus of a different element.
- The energy liberated during radioactive decay comes from within individual nuclei without external excitation, similar to the case of atomic radiation.
- Radioactive decay is a statistical process that obeys the law of chance i.e. a certain probability per unit time.
Law of Radioactive Decay
On emission of or rays, which is usually but not invariably accompanied by - ray emission, the emitting parent nuclei transform into new daughter elements. The daughter element is again radioactive so that the process of successive disintegration continues till parent nuclei transform into stable ones.- Activity: The activity of a sample of any radioactive nuclide is the rate at which the nuclei of its constituent atoms decay.
R = - dN / dt
The minus sign is used to make R a positive quantity since dN / dt is a negative quantity. The SI unit of activity is named after Becquerel:1 becquerel = 1 B q = 1 decay/s
The other unit of activity is Curie(Ci), which is defined as 1 g of radium Ra 88 226 .1 curie = 1 Ci = 3.70 10 10 decay/s = 37 GB q
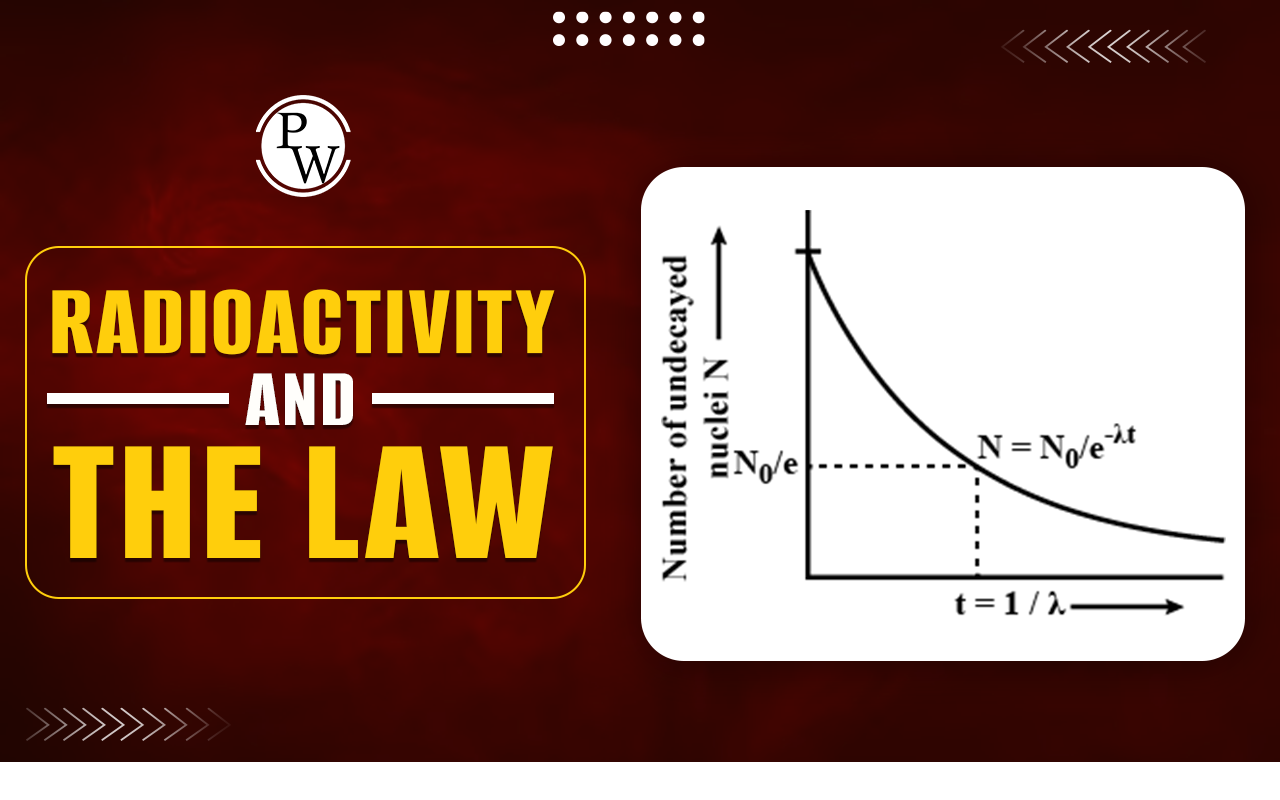
The most important single source is the radioactive gas radon, a decay product of radium traces back to the decay of uranium. Uranium is found in many common rocks such as granite. Hence radon, colorless or odorless, is present nearly everywhere, usually in small amounts to endanger health. As a cause of lung cancer, radon is second only to cigarette smoking. Other natural sources of radiation dosage include cosmic rays from space and radionuclides present in rocks, soil, and building materials. Food, water, and the human body itself contain small amounts of radionuclides of such elements as potassium and carbon. The activities of radioactive samples show that it falls off exponentially with time. When the period starts, the activity drops to half of what it was at the start of the period. Every radionuclide has a characteristic half-life. Some half-lives are only millions of seconds and some are billions of years. One of the major problems faced by nuclear power plants is the safe disposal of radioactive waste since some nuclides have long half-lives. The time variation of activity follows the formulaR = R 0 e - λ t
Whereλ is a decay constant having a different value for each radionuclide.- Half-life: The half-life of a radioactive nuclide is defined as the time T 1/2 in which the actual amount of radioactive atoms is reduced by way of disintegration to half its value. After a half-life has elapsed when t = T 1/2 the activity R drops to 1/2 R 0 . Hence,
1/2R 0 = R 0 e -λT 1/2
e - T 1/2 = 2
Taking logs on both sides, λ T 1/2 = ln2T 1/2 = ln2/ = 0.693/ λ
The larger the decay constant, the greater the chance a given nucleus will decay in a certain period of time. If we assume a constant probability per unit of time for the decay of each nucleus of a given nuclide. With the probability per unit time, dt is the probability that any nucleus will undergo decay in a time interval dt. If a sample contains N undecayed nuclei, the number dN that decays in a time dt is the product of the number of nuclei N and the probability dt that each will decay in dt.dN = -N λ dt
Where the minus sign indicates that N decreases as time increases.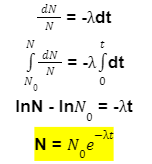 This formula gives the number N of undecayed nuclei at the time t in terms of the decay probability per unit time of the nuclide involved and the number N0 of undecayed nuclei at time t = 0.
Every nucleus in a sample of a radionuclide has a certain probability of decaying but there is no way to know in advance which nuclei will actually decay in a particular time span. If the sample is large enough i.e. many nuclei are present the actual fraction of it that decay in a certain time span will be very close to the probability for any individual nucleus to decay.
This formula gives the number N of undecayed nuclei at the time t in terms of the decay probability per unit time of the nuclide involved and the number N0 of undecayed nuclei at time t = 0.
Every nucleus in a sample of a radionuclide has a certain probability of decaying but there is no way to know in advance which nuclei will actually decay in a particular time span. If the sample is large enough i.e. many nuclei are present the actual fraction of it that decay in a certain time span will be very close to the probability for any individual nucleus to decay.
- Mean Life or Average life: The average or mean lifetime T of all atoms in a given sample is defined as the reciprocal of its decay probability per unit of time:
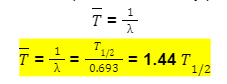 The activity of a radioactive sample is defined as,
The activity of a radioactive sample is defined as,
R = - dN/dt
R = N 0 e - λ t
R = λ NTalk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.











