Diagonal of Rectangle: Meaning, Properties, Formula, and Examples
Diagonal of rectangle is the line connecting opposite corners. Learn the diagonal of a rectangle propertie, and formula to calculate the diagonal length easily.
Chandni 14 Aug, 2025
Share
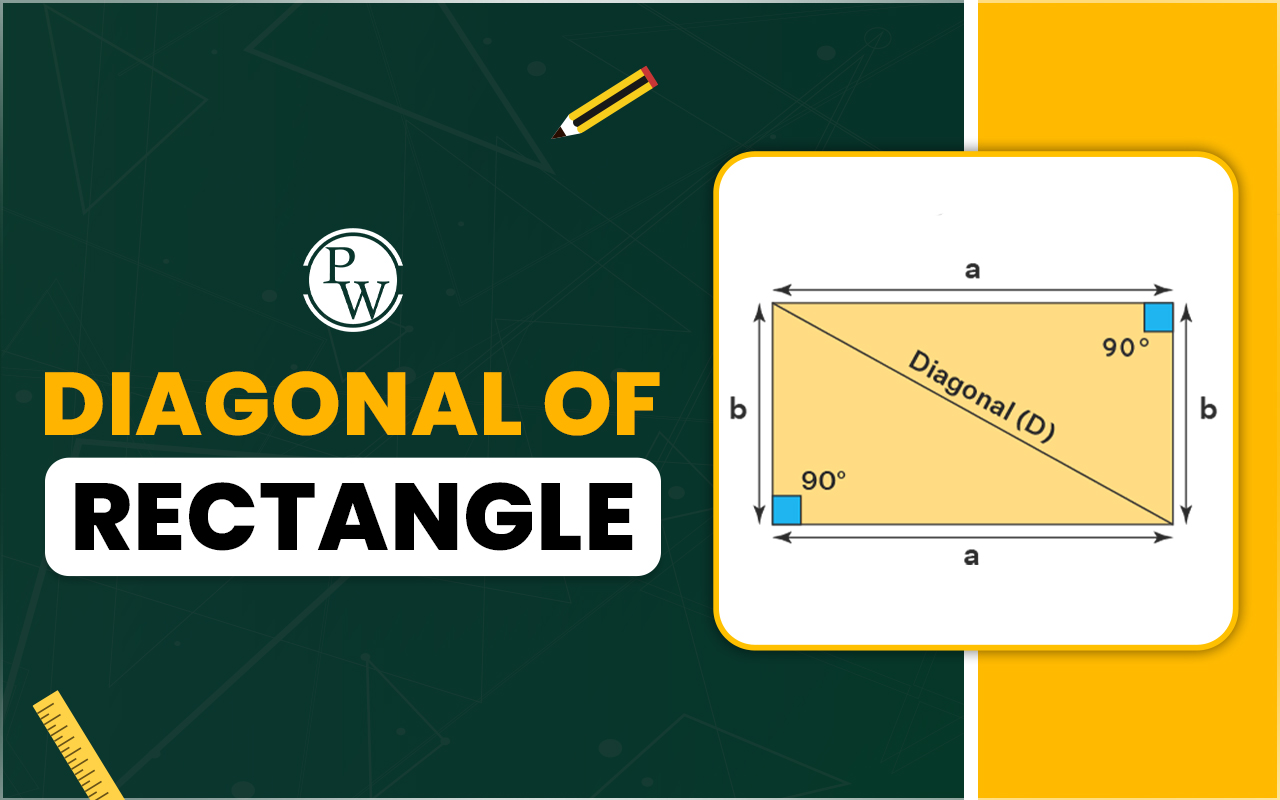
The Diagonal of a rectangle is a very common concept in geometry that becomes handy in different real-life situations, such as identifying the size of a television. This important mathematical concept helps you in various types of scientific calculations and finding quick solutions.
This article gives an idea of the diagonal of a rectangle, its characteristics, and rectangle diagonal formula, along with solved examples for better understanding and applications.What is the Diagonal of Rectangle?
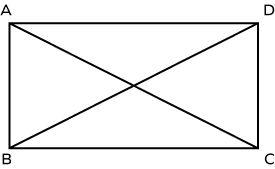In the above figure, ABCD is a rectangle, and its two diagonals are AC and BD, which are equal in length.
Diagonal of Rectangle Properties
The diagonals of a rectangle have some unique properties, which are discussed below. 1. The two diagonals of a rectangle bisect each other at the point of intersection.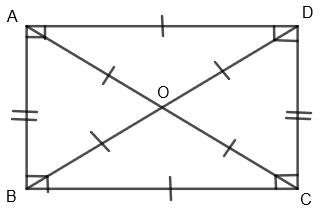
In the above figure, two diagonals bisect each other at point O, so we can say AO = OC and BO = OD. 2. When the diagonals bisect each other, a pair of acute angles and a pair of obtuse angles are formed at the point of intersection.
∠AOD + ∠COD = 180 degrees ∠AOB + ∠BOC = 180 degrees ∠AOB + ∠AOD = 180 degrees ∠BOC + ∠COD = 180 degrees 4. The diagonals divide the rectangle into two equal right-angled triangles. In the above figure, the diagonal AC divides the rectangle into two identical right-angled triangles, ABC and ADC. Similarly, diagonal BD divides the rectangle into two identical right-angled triangles, ABD and BCD 5. The two diagonals of a rectangle divide the rectangle into two pairs of congruent triangles. In the above figure, the triangles AOB and COD are congruent, and triangles AOD and BOC are congruent.
Diagonal of Rectangle Formula
Let's learn how to find diagonal of rectangle. The diagonal of a rectangle divides the rectangle into two right-angled triangles, so it is considered the hypotenuse of these triangles. The formula to find diagonal of rectangle can be obtained using the Pythagoras theorem.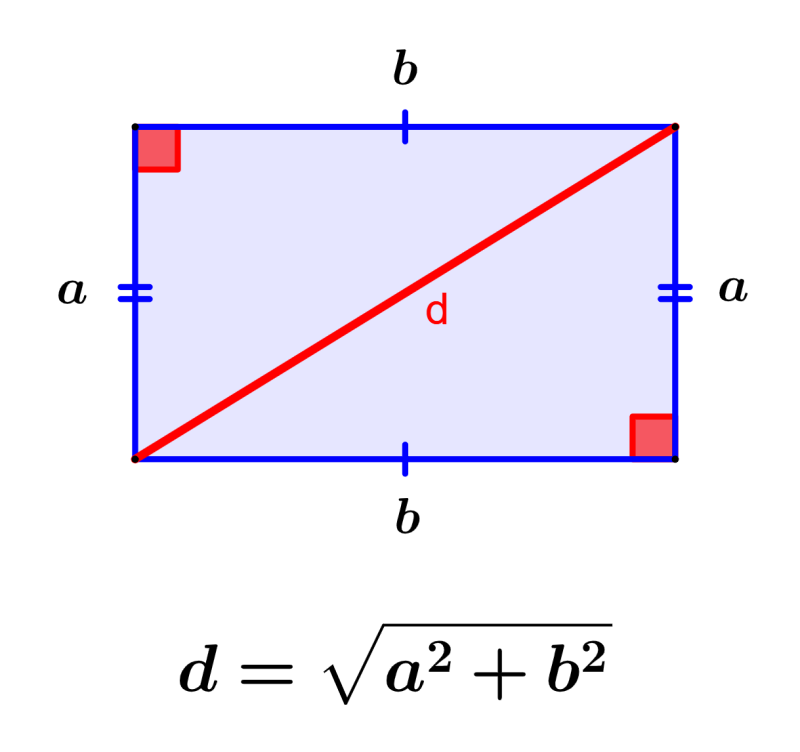
Let us consider a rectangle of length "b" and width "a". Let the length of the diagonal be "d". Applying the Pythagoras theorem, we can write, d 2 = a 2 + b 2 Taking square root on both sides, d = √( a 2 + b 2 )
Thus, the Diagonal of a Rectangle formula is:
d = √( a 2 + b 2 )
Where- d = diagonal of rectangle
- b = length of the rectangle
- a = width of the rectangle
Diagonal of Rectangle Solved Examples
1. Using the diagonal of the rectangle formula, find the diagonal of a rectangular park whose dimensions are 30 ft and 40 ft.
Solution: As per the formula of diagonal, if the length and width of a rectangle are l and w, then the diagonal can be calculated as d = √( l 2 + w 2 ) Here, l = 40 and w = 30 So, diagonal d = √(40) 2 + (30) 2 = √2500 = 50 Answer: The diagonal of the park is 50 ft.2. If a television screen has a length of 30 inches and a width of 20 inches. What is the size of the television?
Solution: The size of the television is the length of its diagonal. The length of the television, l = 30 The width of the television, w = 20 Using the diagonal of a rectangle formula, d = √( l 2 + w 2 ) d = √( 30 2 + 20 2 ) = √1300 = 36.05 Answer: The size of the television is 36.05 inches.3. If a rectangular table has a width of 5 inches with a diagonal of 13 inches. What is the length of the table?
Solution: The width of the table, w = 5 inches. The diagonal of the table, d = 13 inches. Using the diagonal of rectangle formula, d = √( l 2 + w 2 ) or, 13 2 = (l 2 + 5 2 ) or, l 2 + 25 = 169 or, l 2 = 169 -25 or, l 2 = 144 or, l = 12 Answer: The length of the table is 12 inches.4. If the area of a rectangular lawn is 480 square meters and the length is 30 meters, what is the length of the diagonal of the lawn?
Solution: The area of a rectangle is A = Length (l) X Width (w) The length of the lawn, l = 30 and the area, A = 480 Therefore, 450 = 30 x w or, w = 450/30 = 16 So, the width of the lawn is 16 meters. Now, using the diagonal of rectangle formula, we can write Diagonal d = √( l 2 + w 2 ) = √( 30 2 + 16 2 ) = √900 + 256 = √1156 = 34 Answer: The diagonal of the lawn is 34 meters.| Related Articles | |
| Equation | Area of Equilateral Triangle |
| Quadrilateral | Area of Trapezium |
| Ratio | Surface Area of Cylinder |
Diagonal of RectangleFAQs
When can the diagonals of a rectangle intersect at 90 degrees?
The diagonals of a rectangle intersect at 90 degrees when all sides of the rectangle are equal which means it is a square.
Can a rectangle be considered a parallelogram?
A rectangle can be considered a parallelogram with all angles as 90 degrees.
What is the origin of the word diagonal?
The term diagonal is derived from the Greek word ‘diagonios’, which means ‘from angle to angle.’
If the diagonal of a rectangle is twice its width, what is the ratio of its length to width?
If the diagonal of a rectangle is twice its width, the ratio of its length to width is √3.
If the length and width of a rectangle are doubled, how will the length of its diagonal change? Ans
If the length and width of a rectangle are doubled, the length of its diagonal will also become double.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
