Integration of UV Formula: ILATE Rule with Solved Examples
Chandni 14 Jun, 2025
Share
The Integration of UV Formula helps simplify the process of integrating the product of two functions, such as algebraic, trigonometric, or logarithmic expressions. The Integral UV formula is written as:
∫u dv=uv−∫v du
This method, also called integration by parts , breaks down complex integrals into simpler parts using the relationship between differentiation and integration. It’s a practical tool for solving problems where traditional methods may not work easily.
In this blog, we’ll explore the UV formula step-by-step, learn how it’s derived, and look at some examples to help you apply it confidently.
Read More: What is Photosynthesis?
What is the Integration of UV Formula?
The integration of UV formula is a technique used in calculus, specifically in integration by parts, to calculate the integral of the product of two functions. If u(x) and v(x) are two functions and their integral is of the form ∫udv , the integration of uv formula is given by:∫uv dx=u∫v dx−∫(u′∫v dx)dx
or equivalently,∫u dv=uv−∫v du
Here:- u is the first function, and dv (or v′ dx ) is the second function.
- u' is the derivative of u , and ∫v dx represents the integral of v.
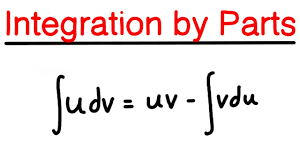To decide which function is u (the first function), the LIATE (or ILATE ) rule is applied. This rule prioritizes the functions in the following order:
- L ogarithmic functions (e.g., lnx )
- I nverse trigonometric functions (e.g., arctanx )
- A lgebraic functions (e.g., x, x 2 )
- T rigonometric functions (e.g., sinx, cosx )
- E xponential functions (e.g., e x , 2 x )
How to Apply the Integration of UV Formula?
The integration of UV formula follows a systematic approach to compute the integral of the product of two functions. Here are the steps explained with an example:Step 1: Identify the functions u(x) and v(x) :
Use the LIATE rule to choose u(x):- L ogarithmic
- I nverse trigonometric
- A lgebraic
- T rigonometric
- E xponential
Step 2. Find the derivative of u(x) :
Compute du/dx, the derivative of u(x), which is written as du. This step simplifies one part of the integral.Step 3: Integrate v :
Find the integral of dv , which gives v(x) . For example, if dv=e x dx, then v=e xStep 4: Substitute into the formula:
Use the integration of UV formula: ∫u⋅v dx=uv−∫v⋅du Plug u(x) , v(x) , and du into the formula to transform the original integral into a simpler one.Step 5: Simplify and Solve:
Compute the remaining integral ∫v⋅du. Combine all terms to get the final solution, including the constant of integration C .Read More - Combustion and Flame
Example : Find ∫xsin(x)dx
We will integrate the product xsin(x) using the UV formula.Step 1: Choose u(x) and dv :
Based on the LIATE rule: u(x)= (algebraic function) dv=sin(x)dx (trigonometric function)Step 2: Differentiate u(x) :
u=x ⟹ du=dxStep 3: Integrate dvdv :
dv=sin(x)dx ⟹ v=−cos(x)Step 4: Substitute into the formula:
∫x sin(x)dx=u⋅v−∫v⋅duSubstituting the values:
∫x sin(x)dx=x⋅(−cos(x))−∫(−cos(x))⋅dx ∫x sin(x)dx=−xcos(x)+∫cos(x)dxStep 5: Simplify and solve:
Integrate ∫cos(x)dx ∫x sin(x)dx=−x cos(x)+sin(x)+C or ∫x sin(x)dx=sin(x) −cos(x) +CDerivation of Integration of UV Formula
Here, we will learn the derivation of the integration of UV Formula using the product rule of differentiation:
Step 1: Start with the product rule of differentiation
Consider two differentiable functions, u and v , such that: y=u⋅vy = Using the product rule of differentiation:
Step 2: Rearrange the equation to isolate u dv/dx on one side:
Step 3: Integrate both sides with respect to x:
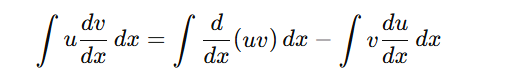
Step 4: Simplify using the fundamental theorem of calculus
The integral of a derivative, ∫d/dx (uv) is simply the original function uv. This gives: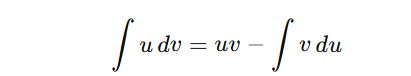
Hence, the formula for integration by parts is derived as: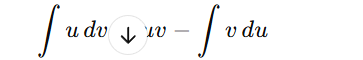 
Read More - Motion and measurement of Distance
Integration of UV Formula Examples
Here are examples solved using the product rule of integration to demonstrate various scenarios where the formula is applied:Example 1: Find the integral of x 2 ⋅ex
Solution:
Identify u and dv : Let u= x 2 , so du=2xdx Let dv=e x dx, so v=∫e x dx=e x Apply the formula ∫u dv=uv−∫v du ∫x 2 e x dx=x 2 e x −∫(2xe x )dx Solve the remaining integral ∫2x ex dx Let u=x, du=d , , v=e Multiply by 2: ∫2xe dx=2(x ex −e x ) Substitute back: ∫x 2 e dx = x 2 e −2(xe −e ) Simplify: ∫x 2 e dx = x 2 e − 2 x e x + 2 e x + CAnswer:
∫x 2 e dx = e ( x 2 − 2 x + 2 ) + CExample 2: Find the integral of ln(x)⋅e x
Solution:
Identify u and dv : Let u=ln(x), so du=1/xdx Let dv=e x dx , so v=∫e x dx=e x vApply the formula ∫u dv=uv−∫v du:
∫ln(x)e x dx=ln(x)⋅e x −∫e x × 1/x dxSimplify the terms:
∫ln(x)e x dx=ln(x)⋅e x −∫e x / xdx The second integral ∫e x dx cannot be expressed in elementary functions, so the answer remains: ∫ln(x)e x dx=ln(x)⋅e x −∫e x /x dx+CIntegration of UV Formula Uses
The integration of UV formula has far-reaching applications in mathematics, physics, and engineering. Beyond solving integrals, it serves as a critical tool in:Differential Equations: Integration by parts is frequently used to solve linear differential equations and boundary value problems where the integrals involve complex functions.
Fourier Series and Transforms: This UV formula simplifies the derivation and evaluation of Fourier coefficients, a cornerstone for signal processing and analyzing periodic functions.
Quantum Mechanics and Physics: In physics, integration by parts appears in the solution of wave equations, Schrödinger's equation, and problems involving energy states.
Numerical Methods: It forms the theoretical base for various approximation methods used in numerical integration and computational calculus.
Machine Learning and AI: The UV formula helps solve integrals of probability density functions and loss functions, essential in algorithms like backpropagation.
By mastering the integration of UV formula, you'll gain a versatile mathematical tool applicable across a wide range of fields, extending its utility far beyond textbook problems. Join Kids Online Tuition Class Now !!Integration of UV Formula AQs
What is another name for the UV formula?
When should the UV formula be used?
How is the UV formula different from substitution?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
