Unit Circle - Equation of a Unit Circle, Definition, Importance

Unit circle is one of the most important ideas in trigonometry. It is a circle with a radius of one, positioned at the center of the coordinate plane. Even though it looks simple, the unit circle helps us understand angles, triangles, and trigonometric functions like sine, cosine, and tangent.

If you are learning trigonometry for the first time, the unit circle can feel confusing at first. But once you learn how it works, you will see that it actually makes many math problems easier to solve.

Here, you will learn about the unit circle in detail, including its equation, its role in trigonometry, angle measures in degrees and radians, quadrant rules, and step-by-step solved examples.

Also read: How many seconds in a day? 

What is Unit Circle?

A unit circle is a circle with a radius of one. The word "unit" means one, so every point on the circle is one unit away from the center. The center of the unit circle is at the point (0, 0) on the coordinate plane, where the x axis and y axis meet. This point is called the origin.

Why is Unit Circle Important?

The unit circle is important because it helps us understand how angles are connected to points on a graph. It also makes it easier to learn and remember sine, cosine, and tangent, which are used in many math problems.

Here are a few key things it helps with:

• It shows how each angle matches a point on the circle

• The x value of the point gives you the cosine of the angle

• The y value gives you the sine of the angle

• These values follow a pattern in all four parts of the circle

The unit circle works with both degrees and radians, so it is useful in many different situations. Once you practice with it, solving trigonometry problems becomes much simpler and faster.

Also read: Basic Algebra - Definition , Meaning, Examples

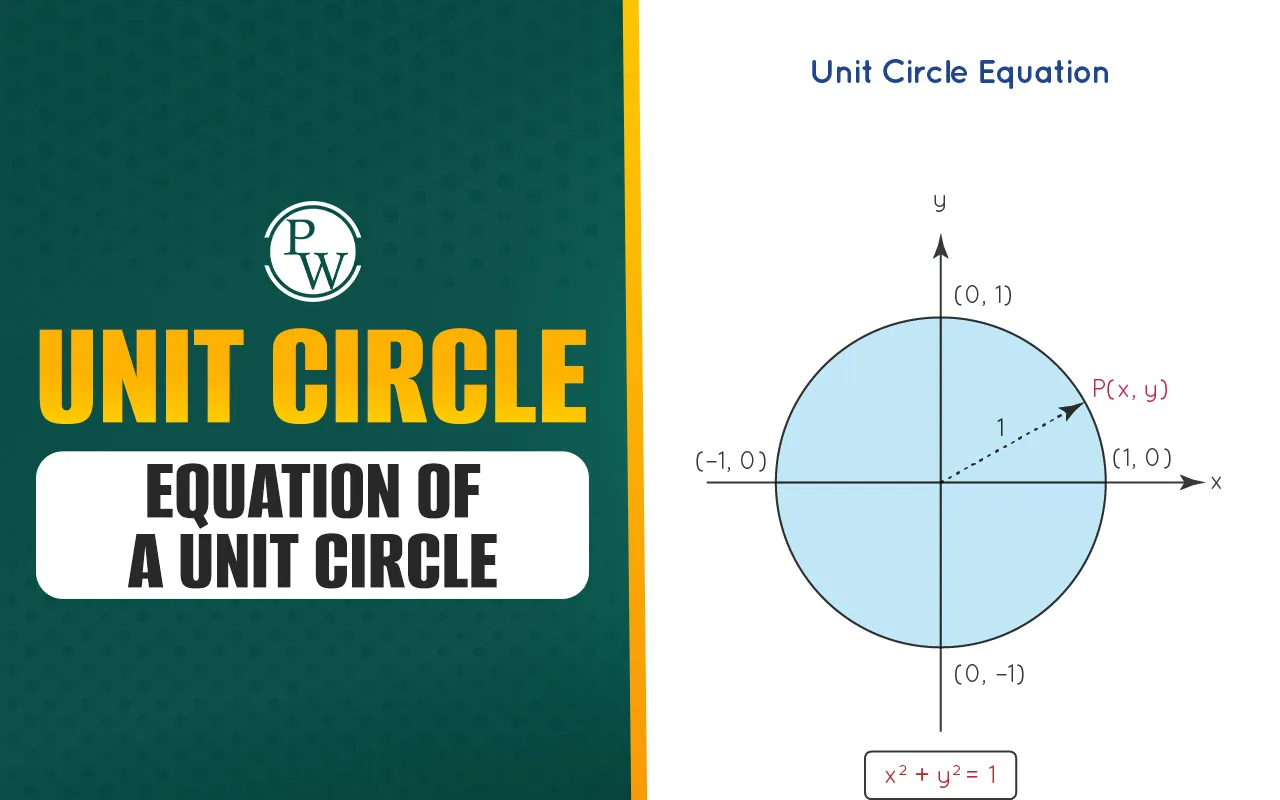
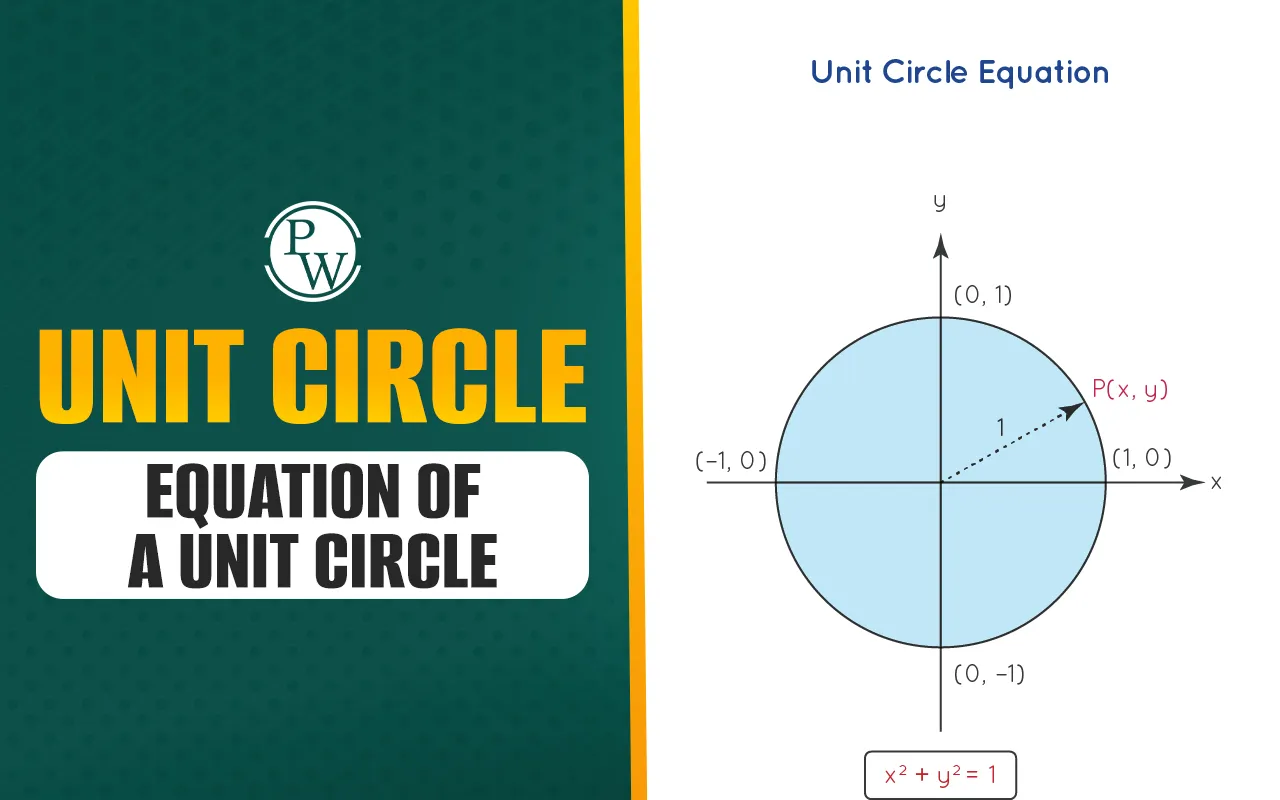
Equation of Unit Circle

The general equation of a circle with center (h,k) and radius r is:

(x − h)2 + (y − k)2 = r2

For a unit circle, the radius r = 1. So the equation becomes:

(x − h)2 + (y − k)2  =1

If the center of the unit circle is at the origin, which means (h,k) = (0,0), then the equation simplifies to:

x2 +  y2 = 1

This is the standard form of the unit circle equation used in trigonometry.

Also read: Introduction to Graphs - Data Types, Graphs

How Unit Circle Connects to Trigonometry?

The unit circle helps us find the values of sine and cosine for different angles.

Start at the center of the circle, which is the point (0, 0). Pick any point on the circle. Draw a straight line from the center to that point. This line creates an angle with the x axis. That angle is called theta.

Now look at the triangle formed. If you draw a line straight down from the point to the x axis, you get a right triangle.

In this triangle:

• The side along the x axis is the value of cosine

• The side going up or down is the value of sine

• The longest side, from the center to the point, is the radius, which is 1

This means:

• The cosine of an angle (theta) is equal to the x-coordinate of the point on the unit circle.

• The sine of an angle (theta) is equal to the y-coordinate of the point on the unit circle.

So every point on the unit circle has the coordinates

(cosine of theta, sine of theta)

This is how the unit circle connects angles to coordinates and helps us understand trigonometry.

Example 1: Find Coordinates at 0°

Let’s apply what we just learned.

At 0°, the point on the unit circle lies directly on the x-axis. That means:

• cos(0°) = 1

• sin(0°) = 0

So the coordinates are (1,0)

Let’s test that in the equation of a unit circle:

x2 + y2 = 1

It is verified!

Also read: Factorial of 100

What are Circular Units (Radians)?

Angles in trigonometry are measured in two ways. One way is in degrees. The other way is in radians, which are also called circular units.

Radians are based on the circle itself. They are connected to the length of the arc that an angle cuts out from the circle.

Here is a quick comparison between degrees and radians:

• 180 degrees is equal to π radians

• 360 degrees is equal to 2π radians

This means that one full turn around the unit circle is 2π radians.

You might see angles written as π over 2, π over 3, or π over 4. These are all radian values, and they are used often in trigonometry when working with the unit circle.

Enroll Now for Kids Online Classes

Four Quadrants and Signs

The unit circle is divided into four parts, called quadrants:

1. Quadrant I (0° to 90°): All trigonometric functions are positive.

2. Quadrant II (90° to 180°): Sine is positive.

3. Quadrant III (180° to 270°): Tangent is positive.

4. Quadrant IV (270° to 360°): Cosine is positive.

This helps you determine the signs of sine, cosine, and tangent depending on where the angle lies.

Also read: HCF and LCM 

Unit Circle Table

The unit circle table shows the values of cosine, sine, and tangent at common angles. These values are used often in trigonometry, and they follow clear patterns. Here are the values for some key angles:

Also read:  Binary to Octal Conversion

Unit Circle Solved Examples

1. What are the coordinates on the unit circle at 180 degrees?

Solution: At 180 degrees, the angle lies on the negative x axis. On the unit circle, this means the point is (−1,0)

So,

• cos(180°) = −1

• sin(180°) = 0

The coordinates are (−1, 0)

2. A point on the unit circle has a y value (sine) of −1. What is the angle in degrees?

Solution: Sine represents the y coordinate.

• The only point where y = −1 is at the bottom of the unit circle

• That point is at 270 degrees

The angle is 270 degrees.

3. Does the point (√2/2,√2/2) lie on the unit circle?

Solution: Use the unit circle equation:

x2  + y2 =1

Substitute the values:

(√2/2) +  (√2/2) = 2/4 + 2/4 = 4/4 = 1

Yes, the point lies on the unit circle.

PW CuriousJr App

3. Show that sin⁡2(θ)+cos⁡2(θ) =1 is always true for the unit circle.

Solution: On the unit circle, every point has coordinates (cos θ, sin θ)

So,

cos⁡2(θ) + sin⁡2(θ) = x2 +y2 = 1

This is the same as the unit circle equation.

4. What is the value of tangent at 225 degrees?

Solution:

225 degrees lies in the third quadrant.

• Reference angle is 45°

• In the third quadrant, both sine and cosine are negative

• sin(45°) = √2/2 → becomes − √2/ 2

• cos(45°) = √2 /2 → becomes − √2/ 2

tan⁡(225°) = sin⁡(225°)cos⁡(225°)= −√2/2−√2/2 = 1

tan(225°) = 1

Also read: Basic Geometrical Ideas 

Give Your Child Best Learning Experience  with CuriousJr 

Is your child having trouble finishing homework or keeping up with lessons after school? CuriousJr’s online tuition classes are here to make your child learning easier and more consistent at home.

Your child will benefit from:

• Live classes where teachers explain each topic step by step, making it easier for children to understand lessons clearly.

• Homework support so your child can complete assignments on time and avoid the stress of unfinished work.

• Quizzes and activities that make learning fun while also helping to remember important concepts better.

• Progress updates that keep you informed about your child’s learning journey and improvements.

• Doubt-clearing help so children can ask questions freely and continue learning without gaps.

 Book a demo class today to know more about our classes.