Competitive Exams

IIT JEE, NEET, ESE, GATE, AE/JE, Olympiad

Only IAS

UPSC, State PSC

School Preparation

Foundation (Class 6-12), Commerce, Arts, CuriousJr (1st - 8th), Science, International Boards

Govt Exam

Judiciary, SSC, Defence, Teaching, JAIIB & CAIIB, BIHAR EXAMS WALLAH, UP Exams, Railway, Nursing Exams, Banking, WB Exams

UG & PG Entrance Exams

MBA, IPMAT, IIT JAM, LAW, CUET UG, UGC NET, GMAT, Design & Architecture, Pharma, CSIR NET, CUET PG, NEET PG

FINANCE

CA, CS, Finance Courses, ACCA

Others

English Wallah, Online Degrees

English Proficiency Test

IELTS, TOEFL

Agriculture

Cuboid: Definition, Shape, Properties, Formulas, and Examples

A cuboid is a 3D shape with six rectangular faces, twelve edges, and eight vertices. Check out cuboid's properties, dimensions, components, and formulas with examples here.

Chandni 17 Jun, 2025

What is Cuboid - A Cuboid is a three-dimensional shape that looks like a rectangular box, with six faces, twelve edges, and eight vertices. It is also called a rectangular prism. All its faces are rectangles, and opposite faces are equal and parallel. This means the shape is balanced and uniform, making it easy to identify.

A cuboid is formed when rectangles are stacked together to create a 3D figure. Each face meets its neighboring faces at right angles, ensuring all edges and corners are well-defined. For instance, if you stack identical books on top of one another, they create a cuboid-like shape. An example of a cuboid in real life is a shoebox. The top and bottom of the box are larger rectangles, while the four sides form the remaining faces. The edges are the straight lines where two faces meet, and the corners where three edges come together are the vertices. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]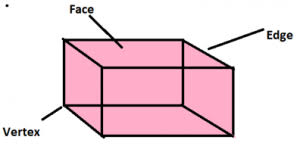

cuboid

Profit and Loss Formula

Cuboid Definition

A cuboid is a three-dimensional shape with six rectangular faces (

, twelve edges (

), and eight vertices (

). It is defined by its length, width, and height, forming a closed structure where opposite faces are equal and parallel. Using Euler’s formula (

This formula confirms the relationship between the faces (

, vertices (

), and edges (

) of a cuboid. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]

Properties of Cuboid

Here are the key properties of cuboid to help you understand it better:

A cuboid has three dimensions: length, width, and height.
It consists of 6 faces, 12 edges, and 8 vertices.
All angles formed at the vertices are right angles (90 degrees).
Opposite edges of the cuboid are parallel to each other.
Each face of a cuboid is a rectangle.
The opposite faces of the cuboid are parallel and congruent.
Each face of a cuboid has two diagonals, connecting opposite corners.

Radius of a Circle

Dimensions of a Cuboid

Let’s learn about the three dimensions of a cuboid that define its shape and size clearly.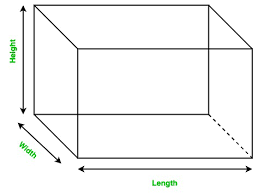

Length (L)

Length is generally considered the longest side of the cuboid. It measures the distance between two vertices along the longest edge. However, this isn’t fixed; a change in orientation can make another side appear as the length. For instance, in a shoebox measuring 15 cm × 10 cm × 8 cm, the 15 cm side is typically identified as the length. When placed upright, the 10 cm side could also be called the length, depending on perspective. This flexibility allows the Cuboid to adapt to different use cases.

Width (W)

The width is the shorter side of the cuboid that goes across it. In the same shoebox, the 10 cm side represents the width, while the 15 cm side is the length. The width is always perpendicular to the length, which helps keep the cuboid in a rectangular shape. This dimension is used for calculating surface area and volume.

Height (H)

Height refers to the side perpendicular to both the length and the width. It defines how tall or deep the cuboid is. For the shoebox example, the 8 cm side is the height when the box is placed flat.

Faces, Edges, and Vertices of a Cuboid

Let’s explore the faces, edges, and vertices that make up a cuboid’s structure.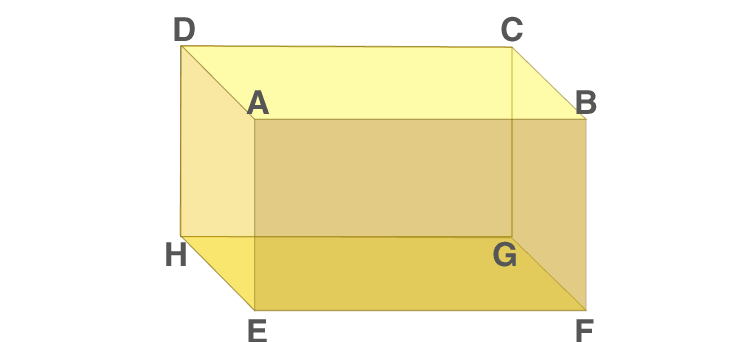 cuboid-shape

Faces

A cuboid has six rectangular faces. In the figure given a bove, these faces are named ABFE, DAEH, DCGH, CBFG, ABCD, and EFGH. In the cuboid figure above, the opposite and parallel faces are:

ABCD and EFGH (the top and bottom faces).
ABFE and DCGH , DAEH and CBFG (the side faces, which are next to the top and bottom).

Edges

Edges are the line segments where two faces meet. A cuboid has 12 edges, and opposite edges are always equal in length. In the cuboid figure above, the edges AB, CD, GH, and EF are equal as they represent the length of the cuboid. Similarly, edges AE, BF, DH, and CG represent the width, while edges AD, BC, EH, and FG define the height. These edges give the cuboid its structure, connecting all the vertices and forming its rectangular framework.

Vertices

Vertices are the points where three edges meet. A cuboid has eight vertices, labeled A, B, C, D, E, F, G, and H in the above figure. These points form the corners of the cuboid and outline its geometric shape.

Diagonal of Cuboid

A cuboid is a 3D shape with two types of diagonals:

Face Diagonal
Space Diagonal

Here’s the description of each type of diagonal for a cuboid:

Face Diagonal

A face diagonal is a straight line that connects two opposite corners of a single rectangular face of the cuboid. Since each face of a cuboid is a rectangle, you can draw two face diagonals on each face. A cuboid has 6 faces, and each face has 2 diagonals, giving a total of 12 face diagonals.

Example: On the top face (ABCD), the diagonals are AC and BD . Similar diagonals can be drawn on the other five faces.

The length of a face diagonal can be calculated using the formula:

Face Diagonal= √l ² +b ²

Where l and b are the dimensions of the rectangle (length and breadth).

Space Diagonal

A space diagonal is a line that connects two opposite corners of the cuboid, passing through its interior. Unlike face diagonals, space diagonals span across the entire cuboid, cutting through its 3D space. A cuboid has 4 space diagonals, as there are 4 pairs of opposite corners. Example: In a cuboid with vertices A, B, C, D, E, F, G, and H, the space diagonals are AG , BH , CE , and DF . The length of a space diagonal is calculated using the formula: Space Diagonal= √l ² + b ² + h ² Where l, b, and h are the length, breadth, and height of the cuboid.

Surface Area and Volume of Cuboid

A cuboid is a 3D shape that looks like a box or a brick, and understanding surface area and volume of cuboid helps us know how much space it covers or holds.

Surface Area of a Cuboid

The surface area of a cuboid is the total area of all its six faces. Since the cuboid is a 3D shape, its surface area depends on three measurements: length (l), breadth (b), and height (h). There are two types of surface area to calculate:

Total Surface Area of a Cuboid (TSA )

This is the total area of all six faces of the cuboid, including the top, bottom, and all the sides.

Total Surface Area of a Cuboid Formula

TSA= 2(lb+bh+lh) square unit

The formula adds the area of the three pairs of opposite faces (length × breadth, breadth × height, and length × height) and multiplies it by 2 because each pair appears twice. Example: For a cuboid with l = 5 units, b = 3 units, h = 4 units l = 5 TSA = 2(5 × 3 + 3 × 4 + 5 × 4) = 2(15 +12 + 20) = 2(47) = 94 square units.

Lateral Surface Area of Cuboid (LSA)

This is the total area of only the side faces, excluding the top and bottom.

Lateral Surface Area of Cuboid Formula

LSA=2h(l+b) square units The formula calculates the area of the four side faces by adding the two vertical sides (height × length) and the two horizontal sides (height × breadth). Example: For a cuboid with l = 5 units, b = 3 units, h = 4 units LSA= 2(4×(5+3)) = 2(4×8)=2(32) =64 square units.

Volume of Cuboid

The volume of cuboid is the amount of space it takes up. This depends on the cuboid’s length, breadth, and height.

Volume of a Cuboid Formula:

Volume (V)=l × b × h cubic units The volume is calculated by multiplying the base area (l×b) with the height. It tells us how much the cuboid can hold. For a cuboid with l = 5 units, b = 3 units, h = 4 units V = 5 × 3 × 4 = 60 cubic units.

Perimeter of Cuboid

The perimeter of cuboid is the total length of all its edges combined. A cuboid has 12 edges, and these edges can be grouped based on their lengths:

Length (l): Edges AB, CD, EF, and GH are equal.
Breadth (b): Edges BC, AD, EH, and FG are equal.
Height (h): Edges CG, BF, AE, and DH are equal.

To calculate the perimeter, we add the lengths of all 12 edges: Perimeter = AB + CD + EF + GH + BC + AD + EH + FG + CG + BF + AE + DH Since there are four edges of each type: Perimeter = (4×l) + (4×b) + (4×h) Simplify this to: Perimeter (P)=4(l+b+h) units For example, if a cuboid has a length of 5 units, a breadth of 3 units, and a height of 2 units, the perimeter would be: P = 4(5+3+2) = 4×10 = 40 units.

Cuboid Formulas

The table below presents the formulas for a cuboid with length (

l

), breadth (

b

), and height (

h

Cuboid Formulas
Measure	Formula
Lateral Surface Area (LSA)	2h(l + b)
Total Surface Area (TSA)	2(lb + bh + hl)
Volume of cuboid	lbh
Perimeter of cuboid	4(l + b + h)
Face Diagonal	√l ² +b ²
Space Diagonal	√l ² + b ² + h ²

Cuboid Solved Examples

Here are a few example problems that use the formulas for cuboids to help understand their properties: Find the volume of a cuboid with a length of 12 cm, breadth of 9 cm, and height of 6 cm. Solution: Given: Length l = 12 cm Breadth (b) = 9 cm Height (h) = 6 cm Volume (V) = l × b × h V = 12 × 9 × 6 = 648 cm ³ . Therefore, t he volume of the cuboid is 648 cm³ .

Calculate the lateral and total surface area of a cuboid with dimensions 15 cm × 10 cm × 8 cm.

Solution: Given: Length (l) = 15 cm Breadth (b) = 10 cm Height (h) = 8 cm Lateral Surface Area (LSA): LSA= 2h(l+b) = 2h(l + b) = 2×8(15+10) =2×8×25 400 cm ² Total Surface Area (TSA): TSA=2(lb+bh+hl) =2(15×10+10×8+8×15) =2(150+80+120) = 2×350=700 cm ² If the length and width of a cuboid are 9 inches and 12 inches, respectively, what is the face diagonal? Solution: Given:

Length (l) = 9 inches
Width (w) = 12 inches

Formula: d = √l ² +w ² Substitute: d = √9 ² +12 ² = √81+144 = √ 225 = 15 inches. The face diagonal is 15 inches . Join Online Tuition Classes for Kids Now !!

Related Articles
Area of Rectangle	Isosceles Triangle
Composite Numbers	Differentiation
Perimeter of Rectangle	Surface Area of Cylinder

Cuboid FAQs

Name three objects in your house that look like cuboids.

A shoebox, a book, and a brick are examples of cuboids because they have six rectangular faces, twelve edges, and eight corners, making them perfect real-life representations of cuboids.

If you cover a cuboid box with wrapping paper, how many faces will you need to cover?

You need to cover six faces of the cuboid to wrap it completely.

You need to fit a shoebox inside a cupboard. Which measurement will you check first: length, breadth, or height?

Check all three measurements to ensure the shoebox fits perfectly.

Can a dice be a cuboid? Why or why not?

No, a dice isn’t a cuboid. It’s a cube because all its sides are equal. A cuboid has unequal length, breadth, and height.

If the base of a cuboid box is square, what can you say about its length and breadth?

The length and breadth must be equal because a square has equal sides.

🔥 Trending Blogs

Diagonal of Rectangle: Meaning, Properties, Formula, and Examples

Profit Formula: Know Easy Ways to Calculate Profit with Examples

The Circulatory System for Kids : Learn Definition, Facts and Examples

What is Punctuation? – Meaning and Definition

Venn Diagram - Examples, Definition, Formula, and Types

Talk to a counsellorHave doubts? Our support team will be happy to assist you!

7019243492

07019243492

Check out these Related Articles

CURIOUS JUNIOR

Division - Meaning, Steps, Algorithm, Examples

Read Full Story

14 Aug 2025, 08:46 pm

CURIOUS JUNIOR

Exponents and Powers - Difference, Examples

Read Full Story

14 Aug 2025, 03:45 pm

CURIOUS JUNIOR

Body Movements: Exploring Human Body Motion with class 6 Explorers

Read Full Story

14 Aug 2025, 12:30 pm

CURIOUS JUNIOR

Food From Where Does It Come: Exploring The Origins Of What We Eat

Read Full Story

14 Aug 2025, 12:28 pm

CURIOUS JUNIOR

Coding and Decoding: Definition, Types, Examples

Read Full Story

13 Aug 2025, 08:38 pm

CURIOUS JUNIOR

Surface Area Formulas: Definitions, Derivations, and Examples

Read Full Story

13 Aug 2025, 01:51 pm

CURIOUS JUNIOR

Ascending Order: Meaning, Symbol, Solved Examples, and Fun Facts

Read Full Story

13 Aug 2025, 06:16 pm

CURIOUS JUNIOR

Median of a Triangle: Definition, Formula, and Examples

Read Full Story

13 Aug 2025, 06:12 pm

CURIOUS JUNIOR

Understanding Light, Shadows, and Reflections with Class 6 physicians

Read Full Story

13 Aug 2025, 01:11 pm

Join 15 Million students on the app today!

Live & recorded classes available at ease

Dashboard for progress tracking

Millions of practice questions at your fingertips

Free Learning Resources

PW Books

Notes (Class 10-12)

Class 10 Math's Notes

Class 10 Chemistry Notes

Class 10 Physics Notes

lass 10 Biology Notes

Aptitude & Reasoning

Class 10 Geography

Physics Class 11 Notes

Class 11 Chemistry Notes

Maths Notes Class 11

Zoology Class 11

Class 11 Botany Notes

Physics Class 12 notes

Chemistry Class 12

Maths Notes Class 12

Zoology class 12

Class 12th Botany Notes

PW Study Materials

Arjuna JEE Study Material

JEE 5 PYQs

JEE Mind Maps

Yakeen Study Material

NCERT Punch

Arjuna Neet Study Material

NEET PYQs

CBSE Sample Paper

CBSE Question Bank

Udaan For Class 10th Study Material

Notes (Class 6-9)

Class-6 Theory & Notes

Math's Notes for class 7

Science Notes for class 7

Class 8 Math Notes

Class 8 Chemistry Notes

Class 8 Physics Notes

Class 8 Biology Notes

Class 8 SST Notes

Class 9 Math's Notes

Class 9 Physics Notes

Class 9 Chemistry Notes

Class 9 Biology Notes

Ncert Solutions

NCERT Solutions For Class 6

NCERT Solutions For class 7

NCERT Solutions for class 8

NCERT Solutions for class 9

NCERT Solutions for class 10

NCERT Solutions for class 11

NCERT Solutions for Class 12

NCERT Solutions For Class 6

Govt Exams

Entrance Exams

Our Other Websites

Class 6th to 12th Online Courses

Class 12 Online Course

Class 11 Online Course

Class 10 Online Course

Class 9 Online Course

Class 8 Online Course

Govt Job Exams Courses

SSC Online Coaching

Bank Exam Online Coaching

TET Online Coaching

JAIIB & CAIIB Online Coaching

Bihar Exam Online Coaching

UPSC Coaching

UPSC Online Coaching

UPSC Offline & Hybrid Coaching

State PSC Online Coaching

UPPSC Online Coaching

BPSC Online Coaching

Defence Exam Coaching

NDA Online Coaching

CDS Online Coaching

AFCAT Online Coaching

Agniveer Online Coaching

Gate Exam Coaching

Civil Engineering Courses

Mechanical Engineering Courses

Formulas

Other Exams

Company Secretary Exam

Know about Physics Wallah

Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.

We Stand Out because

We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.

Our Key Focus Areas

Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.

What Makes Us Different

Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others