Introduction to Force, Moment of a Force

When it comes to understanding how things move and behave in the world of engineering, two concepts take center stage: force and moment of a force. These concepts serve as the building blocks that help us make sense of mechanical systems. These concepts are crucial in understanding how objects move, accelerate, deform, and rotate.

Force Introduction

• “Force is an external agency that either changes or tries to change the state of the motion of the object”. In simpler words “ it is the interaction between the body that can cause a body to change its state of motion, accelerate, decelerate, or deform”.

• Force is described as a vector quantity, possessing both magnitude and direction.
• The SI unit of force is the Newton (N).
• The absence of physical contact does not limit the potential of force to affect the behavior of objects. Force can act on objects from a distance, affecting their motion and deformation without physical contact.

A few examples that illustrate the concept of force: Lifting a box, pushing a door, gravity pulling objects downward, magnets attracting iron, balloons floating in the air, tension in rope, etc.

Characteristics of a Force

A thorough understanding of the characteristics of force is vital because it help us to analyze and predict the behavior of objects when exposed to external forces. A Force has following basic characteristics;

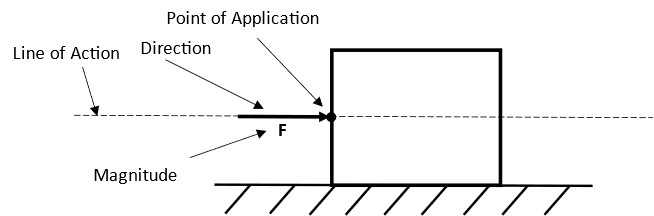
• Magnitude: Force is quantified by its magnitude, which determines the intensity or strength of the force.
• Point of Application: A force is applied at a specific point on an object.
• Line of Action (Direction): The line along which the force acts is an imaginary line passing through the point of application.

Effect of Force on a Body

• A force can alter the motion of a body by either accelerating, maintaining, decelerating, or changing its direction.
• A force Influences the deformation or shape of the body. This deformation, in turn, gives rise to internal stresses within the body.

Moment of a Force

• “ Moment of a force is the measure of tendency of the force to rotate a body about a particular point or axis.” In simpler terms, the moment of a force describes how effectively a force can cause an object to rotate.
• A moment has both magnitude and direction hence moment of a force is a vector quantity.
• In mathematical terms, the moment of a force is calculated as the cross product of two vectors: the vector representing the force and the vector representing the displacement from the point of rotation i.e. position vector.
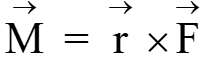
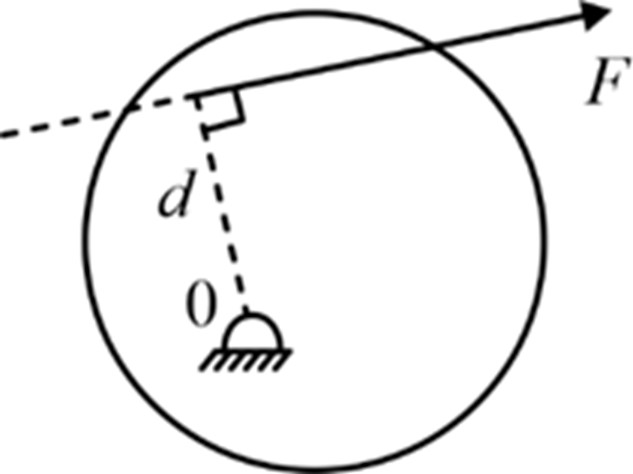
• To simplify calculations, the moment of a force can be determined by multiplying the force magnitude by the perpendicular distance between the line of action of the force and the axis of rotation.

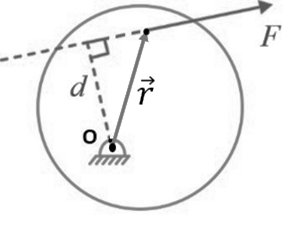
Moment of F about O; M _o =  F × d  (cw)

Where d = Perpendicular distance of line of action of F from O.

• The moment of a force depends on the magnitude of the force, the distance between the point of application and the axis, and the angle between the force vector and the line joining the point of application to the axis. For Example: Imagine a wrench being used to tighten a bolt. When we apply a force to the handle, the bolt experiences a turning effect due to the moment of the force. The magnitude of the moment depends on the force applied and the distance between the axis of rotation (the bolt) and the point of force application (the handle).

Characteristics of Moment of a Force

• Magnitude: Force is quantified by its magnitude, which determines the intensity or strength of the force.
• Point of Application: A force is applied at a specific point on an object.
• Line of Action (Direction): The line along which the force acts is an imaginary line passing through the point of application.
• Axis of Rotation: The "axis of rotation" refers to an imaginary line or point around which an object is capable of rotating. It is the fixed reference point used to calculate the moment of a force.

Direction of Moment of a Force

The direction of the moment of a force plays a crucial role in understanding the rotational effects induced by the force.

• To determine the direction of the moment of a force, you can use a simple method called the right-hand rule. Imagine holding the axis of rotation with your right hand, aligning your fingers in the same direction as the force. Now, curl your fingers naturally. The direction your thumb points to is the direction of the moment vector.
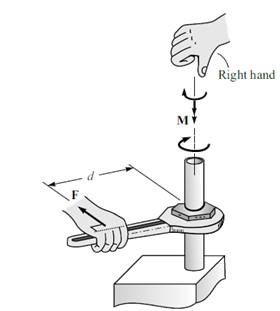
• The direction of the moment vector determines whether the rotation caused by the force is clockwise or counterclockwise. If the moment vector points towards you when viewed along the axis of rotation, the rotation is counterclockwise. Conversely, if the moment vector points away from you, the rotation is clockwise. In provided example, the direction of moment vector is away from you  hence moment having clockwise sense of rotation.

Moment of a Couple

• Couple is caused by two parallel forces of same magnitude and having opposite directions.
• The magnitude of the moment of a couple is given by the product of one of the forces and the perpendicular distance between the lines of action of the forces.

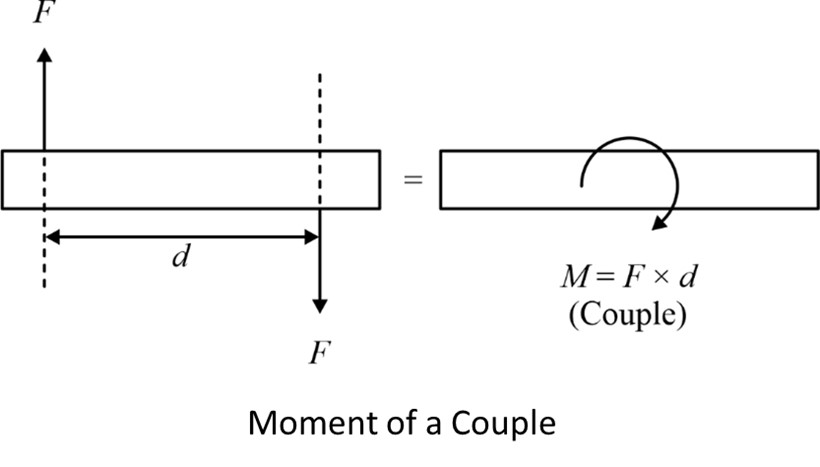
Mathematically, it can be expressed as M = Fd, where M is the moment of the couple, F is the magnitude of either force, and d is the perpendicular distance between the lines of action of the forces.

• The direction of the moment of a couple is perpendicular to the plane formed by the two forces and follows the right-hand rule.
• The moment of a couple is independent of the point about which it is calculated. This means that the rotational effect produced by a couple remains the same regardless of the choice of the point or axis of rotation.