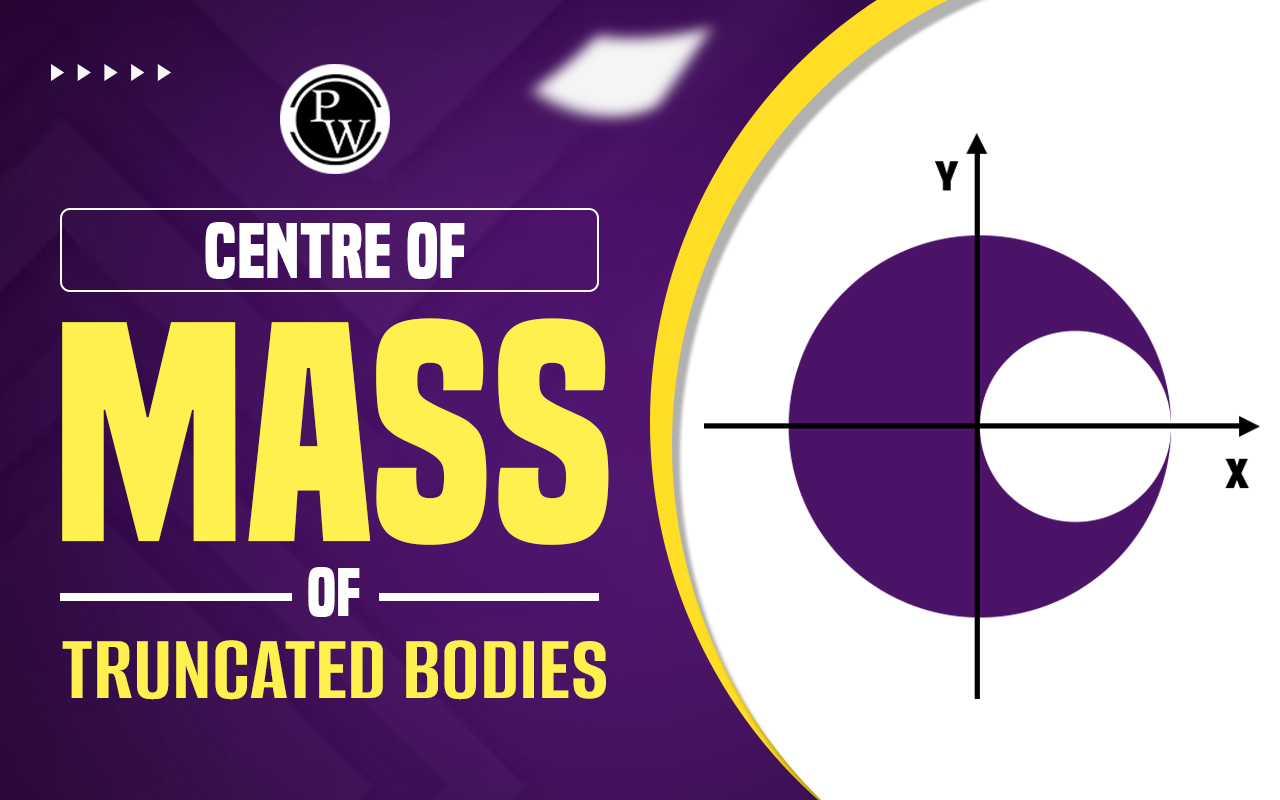
Centre Of Mass Of Truncated Bodies, Centre Of Gravity, Important Points
Centre Of Mass Of Truncated Bodies : We can use the superposition principle to find the center of mass of intersected bodies. If we add the removed part at the same place we get the original body.
Shrivastav 16 Dec, 2023
Share
Centre of Mass of Truncated Bodies
Centre of Mass of Truncated Bodies : Centre of mass of truncated bodies can be found by using superposition principle. If we add the removed portion in the truncated body to get the centre of mass of the original body as shown in the figure.
The removed portion is added to the truncated body keeping their location unchanged relative to the coordinate frame.
Consider the following example to better understand this :
Find the position of centre of mass of the uniform lamina as shown in the figure.
Here, A
1
= area of complete circle = πa
2
A
2
= area of small circle = π
(
x
1
,
y
1
) = coordinates of centre of mass of the large circle = (0, 0)
(
x
2
,
y
2
) = coordinates of centre of mass of the small circle
Using
we get
(as
y
1
and
y
2
both are zero)
Therefore, coordinates of CM of the lamina shown in figure. Are (–
a
/6, 0).
Centre of Mass of Truncated Bodies : Centre of Gravity
Centre of Gravity : We have read that gravitational force between two bodies is always attractive. The earth attracts every particle towards its centre by the force of gravity on the particle which is called the weight W of the
Particle. A body be considered to be made up of a large number of particles of weight W 1 , W 2 , W 3 , ...... As the size of the body is quite small in comparison to the size of t earth, the force of gravity W acting on these particles can be assumed to be parallel to each other as shown in the figure.
All these parallel forces acting in the same direction., vertically downwards towards the centre of the earth) can be replaced by a single force W of magnitude equal to the sum of all these forces i.e., W = W
1
+ W
2
+ W
3
………where W is the total weight of the body. Now the question arises where should the weight W act? This weight is considered to act a point G such that the algebraic sum of moments due to weights W
1
, W
2
, W
3
…. of each particle about G is zero. The point G is called
centre of gravity.
In other words the body can be considered as a point particle of weight W placed at its centre of gravity G.
Thus, the centre of gravity (
C
.
G
.) of a body is the point about which the algebraic sum of moments of weights of all the particles constituting the body is zero. The entire weight of the body can be considered to act at this point, howsoever the body is placed.
Important Points to be noted about Centre of Mass of Truncated Bodies
(i) The position of centre of gravity of the body of a given mass depends on its shape i.e., on the distribution of mass (of particles) in it.
Ex. The centre of gravity of a uniform wire is at the middle of its length. But if the same wire is bent into the form of a circle, its centre of gravity will then be at the centre of circle.
(ii) It is not necessary that the centre of gravity always be within the material of the body.
Ex. The centre of gravity of a ring or a hollow sphere lies at its centre where there is no material.
Centre of gravity of some regular uniform objects
| Centre of gravity of some regular uniform objects: | ||
| Object | Position of centre of gravity | |
| 1. | Rod | Mid-point of rod (Fig 1.37) |
| 2. | Circular disc | Geometric centre (Fig 1.37) |
| 3. | Solid or hollow sphere | Geometric centre of the sphere |
| 4. | Solid or hollow cylinder | Mid-point on the axis of cylinder |
| 5. | Solid cone | At a height h /4 from the base, on its axis (if h = height of cone). |
| 6. | Hollow cone | At a height h /3 from the base, on its axis (if h = height of cone). |
| 7. | Circular ring | Centre of ring (Fig 1.37) |
| 8. | Triangular lamina or scalene triangle | The point of intersection of medians (Fig 1.37) |
| 9. | Parallelogram lamina, square or rhombus | The point of intersection of the diagonals (Fig 1.37) |
Centre of gravity of some regular objects
Centre Of Gravity And The Balance Point
Centre Of Gravity And The Balance Point : A solid body can be balanced by supporting it at its centre of gravity. For example, a uniform metre rule has its centre of gravity at the 50cm mark. It can be balanced on a knife edge keeping it exactly at 50cm mark as shown in the figure. It is possible because the algebraic sum of moments of the weights of all particles of rule about the knife edge is zero.
Similarly, a square lamina can be balanced on the tip of the nail as shown in the figure.
If a body is suspended freely from a point and comes to rest, then in such a position its centre of gravity lies vertically below the point of suspension. This fact can be used to locate the centre of gravity of an irregular lamina.
Determination of centre of gravity using a Plumb line method
Consider an irregular lamina as shown in the figure. Make three fine holes at a, b and c near the edge of the lamina. Check the lamina is free to rotate on the nail about the point of suspension. When the lamina comes to rest draw a line ad along the plumb line. Repeat the procedure by suspending the lamina about cf and eb respectively. The point where all three lines meet will give you centre of gravity.
Centre Of Mass Of Truncated Bodies FAQs
Q.1: State a factor on which position of centre of gravity depends.
Ans. It depends on the distribution of mass.
Q. 2: What is position of centre of gravity of a rectangular lamina?
Ans. At the point of intersection of diagonals.
Q.3. Define the term centre of gravity.
Ans. The centre of gravity (C. G.) of a body is the point about which the algebraic sum of moments of weights of all the particles constituting the body is zero. The entire weight of the body can be considered to act at this point, howsoever the body is placed.
Q. 4. State whether the following statements are true of false.
(i) ‘The position of centre of gravity of a body remains unchanged even when the body is deformed’.
Ans- True
Q.5. The centre of gravity of a hollow cone of height h is at distance x form its vertex where the value of x is
(a) h/3
(b) h/4
(c) 2h/3
(d) 3h/4
Ans- (c) 2h/3
Q.6. Can centre of gravity of a body lie outside of its surface? If yes give example
Ans. Yes. Centre of gravity of a ring lies in its hollow region.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App